【数据结构】用Java实现二叉搜索树(二分搜索树)
目录
1. 概念
2. 具体实现
2.1 MyBST类
2.2 插入
2.3 查找树的最大值
2.4 查找树的最小值
2.5 查找任意值
2.6 删除最大值
2.7 删除最小值
2.8 删除任意值
2.9 普通中序打印输出
2.10 美观的中序打印输出
3. 整体代码
4. 性能分析
4.1 理论分析
4.2 代码实测
4.2.1 生成随机数组与近似有序的数组
4.2.2 测试代码
4.2.3 测试结果
1. 概念
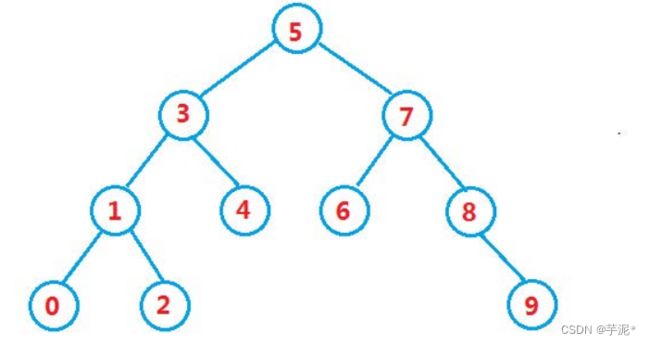
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
- 一般来说二叉搜索树不存在重复的元素(JDK中的二叉搜索树也不存在重复的元素)
2. 具体实现
2.1 MyBST类
public class MyBST {
private TreeNode root;
private int size;
static class TreeNode {
int val;
TreeNode left;//左孩子的引用
TreeNode right;//右孩子的引用
public TreeNode(int val) {
this.val = val;
}
}
}2.2 插入
(1)如果树为空树,即根 == null,直接插入
(2)如果树不是空树,按照查找逻辑确定插入位置,插入新结点(val < root.val,在root的左子树中插入;val > root.val,在root的右子树中插入)(默认不存在重复的元素)
public void add(int val){
root = add(root,val);
}
// 插入一个新的值val,
private TreeNode add(TreeNode root, int val) {
if (root == null){
TreeNode node = new TreeNode(val);
size++;
return node;
} else if (val < root.val) {
root.left = add(root.left,val);
return root;
}
root.right = add(root.right,val);
return root;
}2.3 查找树的最大值
树为空,返回null
树的最大值在数的最右边
// 找最大,树的最右节点
public int Max(){
if (root == null){
throw new NoSuchElementException("bst is empty! Do no has max node");
}
TreeNode node = findMax(root);
return node.val;
}
private TreeNode findMax(TreeNode root){
if(root.right == null){
return root;
}
return findMax(root.right);
}2.4 查找树的最小值
树为空,返回null
树的最小值在数的最左边
// 找最小,树的最左节点
public int Min(){
if (root == null){
throw new NoSuchElementException("bst is empty! Do no has max node");
}
TreeNode node = findMin(root);
return node.val;
}
private TreeNode findMin(TreeNode root){
if(root.left == null){
return root;
}
return findMin(root.left);
}2.5 查找任意值
树为空,返回false
val == root.val 找到了,返回true;
val < root.val,在root的左子树找;
val > root.val,在root的右子树找
// 查找任意值
public boolean contains(int val){
return contains(root,val);
}
private boolean contains(TreeNode root, int val) {
if(root == null){
return false;
}
if(root.val == val){
return true;
} else if (root.val > val) {
return contains(root.left,val);
}
return contains(root.right,val);
}
2.6 删除最大值
找到树的最大值,返回它的左子树节点
// 删除最大值
public int removeMax(){
TreeNode node = findMax(root);
root = removeMax(root);
return node.val;
}
private TreeNode removeMax(TreeNode root) {
if(root.right == null) {
TreeNode left = root.left;
root = root.left = null;
size--;
return left;
}
root.right = removeMax(root.right);
return root;
}2.7 删除最小值
找到树的最小值,返回它的右子树节点
// 删除最小值
public int removeMin(){
TreeNode node = findMin(root);
root = removeMin(root);
return node.val;
}
private TreeNode removeMin(TreeNode root) {
if(root.left == null){
TreeNode right = root.right;
root.right = root = null;
size--;
return right;
}
root.left = removeMin(root.left);
return root;
}2.8 删除任意值
(1)找到需要删除的节点(2)需要删除的节点的左子树为空,返回右子树(可能也为空);需要删除的节点的右子树为空,返回左子树;需要删除的节点的左右子树都不为空:需要使用替换法进行删除,即在它的右子树中找最小值,用它的值填补到被删除节点中,再来处理该结点的删除问题(或者在左子树中找最大值)需要删除的节点的右子树中的最小值:需要删除的节点的左子树的每一个值都比它小
// 删除任意值 Hibbard Deletion 1962
public void removeValue(int val){
remove(root,val);
}
private TreeNode remove(TreeNode root, int val) {
if(root == null){
return null;
} else if (val < root.val) {
root.left = remove(root.left,val);
return root;
}else if (val > root.val){
root.right = remove(root.right,val);
return root;
}else {
if(root.left == null){
TreeNode right = root.right;
root.right = root = null;
size--;
return right;
}else if (root.right == null){
TreeNode left = root.left;
root.left = root = null;
size--;
return left;
}
TreeNode suor = findMin(root.right);
// 移除右子树的最小值时维护了size属性~
// 一定要先删除再连左子树
suor.right = removeMin(root.right);
suor.left = root.left;
root.left = root.right = root = null;
return suor;
}
}2.9 普通中序打印输出
public void print(){
print(root);
}
private void print(TreeNode root) {
if (root == null){
return;
}
print(root.left);
System.out.print(root.val + " ");
print(root.right);
}2.10 美观的中序打印输出
// toString打印
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
generateBSTString(root,0,sb);
return sb.toString();
}
private void generateBSTString(TreeNode root, int depth, StringBuilder sb) {
if(root == null){
sb.append(generateDepthString(depth) + "null\n");
return;
}
sb.append(generateDepthString(depth) + root.val + "\n");
generateBSTString(root.left,depth + 1,sb);
generateBSTString(root.right,depth + 1,sb);
}
// 打印--
// 层数越深,--越多
private String generateDepthString(int depth) {
StringBuilder res = new StringBuilder();
for (int i=0; i3. 整体代码
import java.util.NoSuchElementException;
/**
* 二分搜索树,一般不存相同值的元素
*/
public class MyBST {
private TreeNode root;
private int size;
static class TreeNode {
int val;
TreeNode left;//左孩子的引用
TreeNode right;//右孩子的引用
public TreeNode(int val) {
this.val = val;
}
}
public void add(int val){
root = add(root,val);
}
// 插入一个新的值val,
private TreeNode add(TreeNode root, int val) {
if (root == null){
TreeNode node = new TreeNode(val);
size++;
return node;
} else if (val < root.val) {
root.left = add(root.left,val);
return root;
}
root.right = add(root.right,val);
return root;
}
// 找最大,树的最右节点
public int Max(){
if (root == null){
throw new NoSuchElementException("bst is empty! Do no has max node");
}
TreeNode node = findMax(root);
return node.val;
}
private TreeNode findMax(TreeNode root){
if(root.right == null){
return root;
}
return findMax(root.right);
}
// 删除最大值
public int removeMax(){
TreeNode node = findMax(root);
root = removeMax(root);
return node.val;
}
private TreeNode removeMax(TreeNode root) {
if(root.right == null) {
TreeNode left = root.left;
root = root.left = null;
size--;
return left;
}
root.right = removeMax(root.right);
return root;
}
// 找最小,树的最左节点
public int Min(){
if (root == null){
throw new NoSuchElementException("bst is empty! Do no has max node");
}
TreeNode node = findMin(root);
return node.val;
}
private TreeNode findMin(TreeNode root){
if(root.left == null){
return root;
}
return findMin(root.left);
}
// 删除最小值
public int removeMin(){
TreeNode node = findMin(root);
root = removeMin(root);
return node.val;
}
private TreeNode removeMin(TreeNode root) {
if(root.left == null){
TreeNode right = root.right;
root.right = root = null;
size--;
return right;
}
root.left = removeMin(root.left);
return root;
}
// 查找任意值
public boolean contains(int val){
return contains(root,val);
}
private boolean contains(TreeNode root, int val) {
if(root == null){
return false;
}
if(root.val == val){
return true;
} else if (root.val > val) {
return contains(root.left,val);
}
return contains(root.right,val);
}
// 删除任意值 Hibbard Deletion 1962
public void removeValue(int val){
remove(root,val);
}
private TreeNode remove(TreeNode root, int val) {
if(root == null){
return null;
} else if (val < root.val) {
root.left = remove(root.left,val);
return root;
}else if (val > root.val){
root.right = remove(root.right,val);
return root;
}else {
if(root.left == null){
TreeNode right = root.right;
root.right = root = null;
size--;
return right;
}else if (root.right == null){
TreeNode left = root.left;
root.left = root = null;
size--;
return left;
}
TreeNode suor = findMin(root.right);
// 移除右子树的最小值时维护了size属性~
suor.right = removeMin(root.right);
suor.left = root.left;
root.left = root.right = root = null;
return suor;
}
}
// 普通打印
public void print(){
print(root);
}
private void print(TreeNode root) {
if (root == null){
return;
}
print(root.left);
System.out.print(root.val + " ");
print(root.right);
}
// toString打印
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
generateBSTString(root,0,sb);
return sb.toString();
}
private void generateBSTString(TreeNode root, int depth, StringBuilder sb) {
if(root == null){
sb.append(generateDepthString(depth) + "null\n");
return;
}
sb.append(generateDepthString(depth) + root.val + "\n");
generateBSTString(root.left,depth + 1,sb);
generateBSTString(root.right,depth + 1,sb);
}
private String generateDepthString(int depth) {
StringBuilder res = new StringBuilder();
for (int i=0; i4. 性能分析
4.1 理论分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则 二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
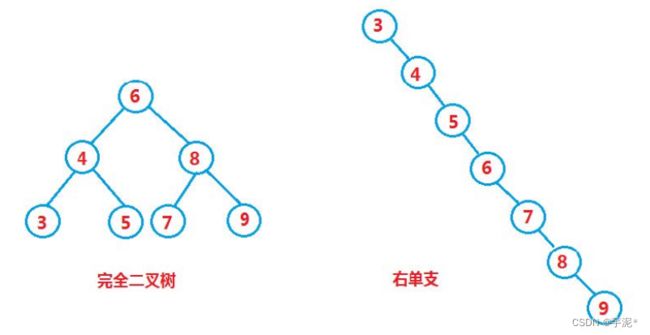
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为:
最差情况下,二叉搜索树退化为单支树,其平均比较次数为:
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,都可以是二叉搜索树的性能最佳?答:TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set ;实际上用的是红黑树,而红黑树是一棵近似平衡的二叉搜索树,即在二叉搜索树的基础之上 + 颜色以及红黑树性质验证。关于红黑树的内容后序再进行讲解,现在只简单使用一些。
4.2 代码实测
4.2.1 生成随机数组与近似有序的数组
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;
public class ArrayUtil {
private static ThreadLocalRandom random = ThreadLocalRandom.current();
// 生成一个大小为n的近乎有序的数组
// 数组的有序与否取决于元素的交互次数
public static int[] generateSortedArray(int n,int swapTimes){
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = i + 1;
}
for (int i = 0; i < swapTimes; i++) {
int x = random.nextInt(0,n);
int y = random.nextInt(0,n);
swap(arr,x,y);
}
return arr;
}
private static void swap(int[] arr,int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
// 生成一个大小为n的随机数数组
// 随机数的取值范围为[l..r)
public static int[] generateRandomArray(int n,int l,int r){
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = random.nextInt(l,r);
}
return arr;
}
// 深拷贝数组
public static int[] arrCopy(int[] arr) {
return Arrays.copyOf(arr,arr.length);
}
}
4.2.2 测试代码
测试红黑树只需要将二分搜索树的代码注释掉,换成红黑树的就好(代码中我已经给了哪些是二分搜索树的代码,哪些是红黑树的代码)
import MyBST;
import java.util.LinkedList;
import java.util.TreeMap;
import static util.ArrayUtil.generateRandomArray;
import static util.ArrayUtil.generateSortedArray;
public class BSTPerformanceTest {
public static void main(String[] args) {
LinkedList list = new LinkedList<>();
// 红黑树又称红-黑二叉树,红黑树是一颗自平衡的排序二叉树。
// TreeMap bst = new TreeMap<>();
渐进有序的数组
// int n = 10_0000;
// int[] arr = generateSortedArray(n,50);
// 二分搜索树
MyBST bst = new MyBST();
// 乱序的数组
int n = 100_0000;
int[] arr = generateRandomArray(n,0,Integer.MAX_VALUE);
System.out.println("-----------------------插入-----------------------------");
Long start = System.nanoTime();
for (int i:arr
) {
list.add(i);
}
Long end = System.nanoTime();
System.out.println("链表插入" + (end - start)/1000000.0 + " ms");
start = System.nanoTime();
for (int i:arr
) {
// 二叉树搜索树
bst.add(i);
// 红黑树
// bst.put(i,i);
}
end = System.nanoTime();
System.out.println("BST插入" + (end - start)/1000000.0 + " ms");
// System.out.println("红黑树插入" + (end - start)/1000000.0 + " ms");
System.out.println("-----------------------查询-----------------------------");
start = System.nanoTime();
list.contains(999);
end = System.nanoTime();
System.out.println("链表查询" + (end - start)/1000000.0 + " ");
start = System.nanoTime();
// 二叉树搜索树
bst.contains(999);
// 红黑树
// System.out.println(bst.containsKey(999));
end = System.nanoTime();
System.out.println("BST查询" + (end - start)/1000000.0 + " ");
// System.out.println("红黑树查询" + (end - start)/1000000.0 + " ");
}
}
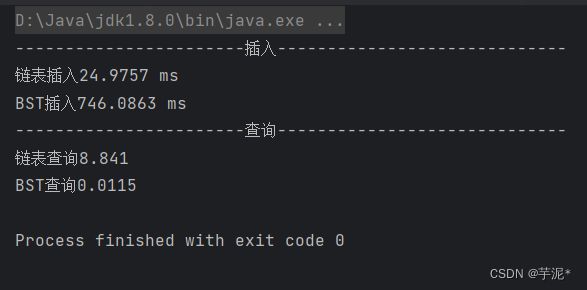
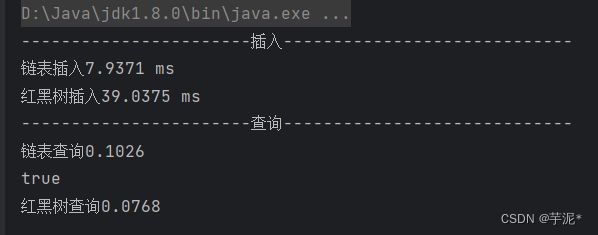
4.2.3 测试结果
二分搜索树与链表性能测试
红黑树与链表性能测试