ComputerInBook

Fourier分析入门——第3章——离散函数的Fourier分析

第 3 章离散函数的Fourier分析

3.1 引言

3.2 在1点采样的函数

3.3 在2点采样的函数

3.4 Fourier分析是一种线性变换

3.5 Fourier分析是一种基向量的变更

3.6 在3点采样的函数

3.7 在D点采样的函数

3.8 整理(tidying up)

3.9 Parseval[pá:zeifa:l]定理

3.10 关联统计

3.11 图像对比和复合光栅(Image Contrast and Compound Gratings)

3.12 闭合曲线形状的Fourier描述符(Fourier Descriptors of the Shape of a Closed Curve)

第 3 章离散函数的Fourier分析

3.1 引言

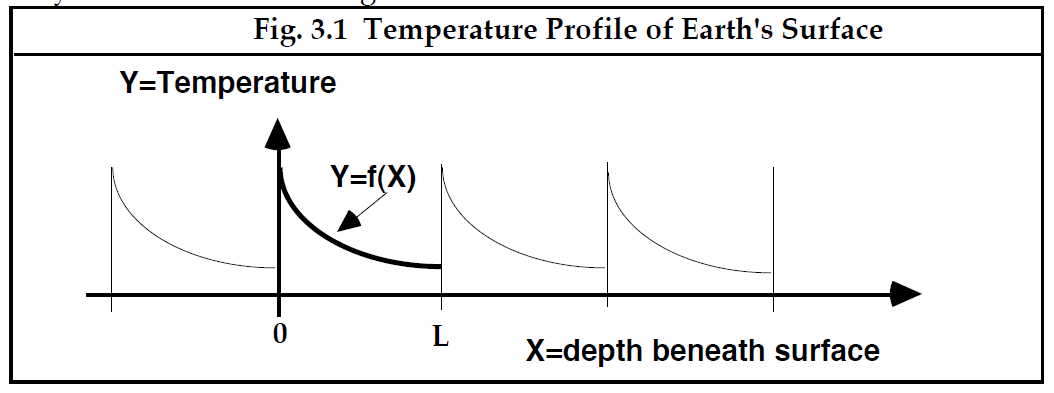
Carslaw (1921)在他的经典教材<>(Fourier级数和积分理论)中介绍历史时，回顾了18 世纪中叶关于任意函数是否可以表示为一系列加权正弦曲线之和的激烈争论(controversy raging)。许多欧洲最著名的数学家都参加了辩论，包括Euler、D'Alembert、Bernoulli、Lagrange、Dirichlet和Poisson。那时，人们认识到周期函数(如弦的振动)可以用三角级数表示。然而，完全不清楚非周期函数是否可以这样表示，特别是如果它需要无限数量的正弦和余弦，而这些正弦和余弦不一定会收敛于某个稳定的总和。因解决这个问题而受到赞誉的Fourier对热传导理论(theory of heat)很感兴趣。数学问题及其实际应用的核心问题是了解地球在地表以下不同深度的温度分布。典型的曲线 = f (X) 可能看起来像图 3.1 中所示的粗曲线(heavy curve)所示

(译注： = 地表以下的深度， = 温度)

------------------------图 3.1地球表面的温度曲线-----------------------------

尽管此示例中的温度分布仅定义为从地球表面 ( = 0) 到深度 = ，但假设我们多次复制给定曲线并将各段首尾相连，如图中的细曲线(light curves)所示。结果将是一个周期为的周期函数，可以在正向和负向轴方向上任意拉伸。这种人为制造的周期性旨在提高我们对采用正弦曲线之和表示此类函数成功的期望，正弦曲线覆盖轴的整个长度。显然，如果正弦曲线之和适合整个轴上的周期函数，则它会适合用于区间 (0 - ) 内的原始函数。该图还清楚地表明每个正弦分量的周期必须是的某个倍数，否则某些间隔将与其他间隔不同，这与周期性的思想不相容。精确重现函数 = f (X) 所需的呈谐波关系的正弦级数的名称就是Fourier级数(series)(译注：Fourier级数就是一系列呈谐波关系的正弦级数，这些正弦函数之间的频率是倍频关系，即都为某个基波频率的整数倍)。

在解决为有限区间上定义的连续函数求Fourier级数这一难题之前，我们将从更简单的问题开始——即当给定函数由沿 轴均匀分布的 值的离散序列组成时所确定的Fourier级数。对于需要分析某些物理变量的一系列离散测量值，或者可能使用计算机以规律的时间间隔对连续过程进行采样的实验者来说，这个问题不仅更容易，而且更具有实际意义。

3.2 在1点采样的函数

考虑一种极端情况，其中函数 ( ) 仅已知的一个值。例如，在图 3.1 所示的热研究中，假设我们有一个由在 = 0位置采样得到的单个测量值 $_{0}$ $\mathsf{Y}_{0}$ 组成的原始数据集。为了体验未来更具挑战性的案例的味道，设想一下对这个单一的测量值进行建模的函数

Y = f ( X ) = m -------------------------------------------------------[3.1]

其中，m 是一个我们必须确定的数值参数。很明显，这个选择是令 $m = \mathsf{Y}_{0}$ 。该问题在图 3.2 中以图形方式说明，问题的解是通过基准点的粗水平线。这条水平线是D = 1个样本这种情况Fourier级数，参数 m 称为Fourier系数(coefficients)。虽然这是Fourier分析的一个相当简单的例子，但它说明了更通用过程的第一步。

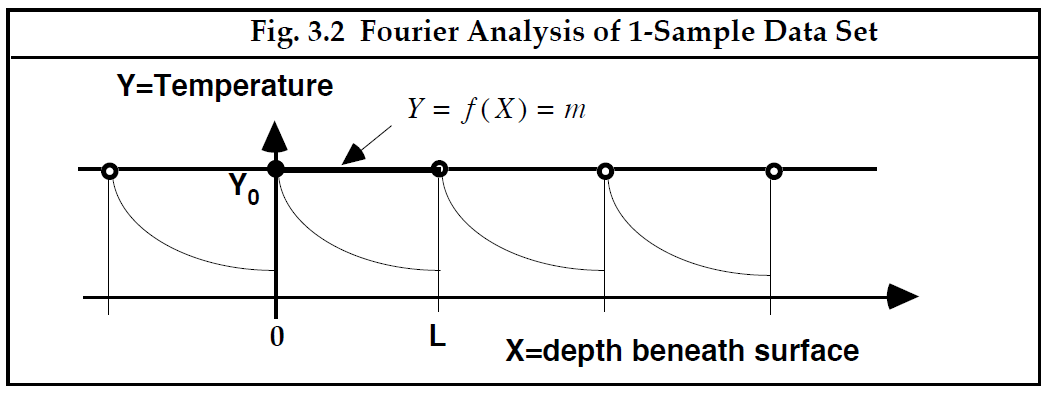
---------------------------图 3.2 一个采样点数据集的Fourier分析-------------------------------------------

如果我们参与复制数据集的过程是为了产生周期函数，则相同的Fourier级数会按预期通过所有复制的数据点。但是请注意，拟合线(fitted line)对潜在连续曲线的表示非常差。当然，原因在于我们只提供了一个测量值；为了更好地适配潜在的函数，我们需要更多样点。

3.3 在2点采样的函数

接下来，假设我们分别在两个深度 $\mathsf{X} = 0$ 和 $\mathsf{X}=\mathsf{L}/2$ 采样得到两个测量值 $\mathsf{Y}_0$ 和 $\mathsf{Y}_1$ ，如图3.3所示。这些值对应将整个区间 $\mathsf{L}$ 按 D = 2 等分的前两个子区间。现在我们获得了两个测量值，我们就可以在我们的模型中加入第二个采样值。因此，我们寻求适配数据的Fourier级数为(译注：这个余弦项的引入稍显突兀，如果有个过度过程或许更好)

$Y=f(X)=m+a.cos(2\pi \mathsf{X}/ \mathsf{L})$ 。------------------------------------------[3.2]

为了确定未知的Fourier系数 m 和 a ，我们使用已有的两个值来计算方程[3.2]。结果是这一对方程

$\mathsf{Y}_0 = m + a.cos( 0 ) = m + a$ ..........................@ = 0

$\mathsf{Y}_1=m + a.cos(\pi) = m - a$ ..........................@ = /2 --------------[3.3 ]

这对方程的解是

$m = \frac{\mathsf{Y}_0+\mathsf{Y}_1}{2}$

$a = \frac{\mathsf{Y}_0-\mathsf{Y}_1}{2}$ -----------------------------------------------------------------------------------------[3.4]

因此，我们总结出这个模型为

$Y = \frac{\mathsf{Y}_0+\mathsf{Y}_1}{2}+\frac{\mathsf{Y}_0-\mathsf{Y}_1}{2}.cos(2\pi \mathsf{X}/ \mathsf{L})$ -------------------------------------------[3.5]

将正好通过原来的两个数据点，如下图3.3所求。

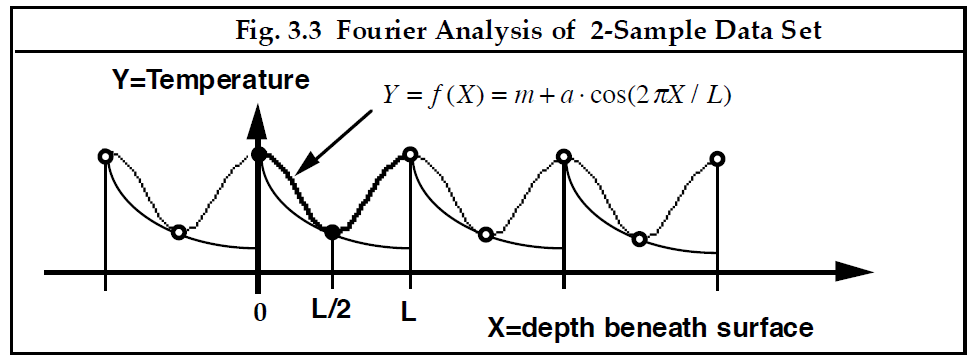
---------------------------图 3.3 一个采样点数据集的Fourier分析-----------------------------------------------

注意，该模型中的余弦项在区间 (0-L) 中经历了一个完整的循环。换句话说，余弦项的频率与潜在函数的周期波形的频率相同。基于这个原因，这个余弦被称为Fourier级数中的基本谐波项(fundamental harmonic term)(译注：复杂有规律周期波的分量，“谐”指“和声”，“有规律的声音”，相对于杂乱无章的噪声而言，这些分量之间的频率呈整数倍关系)。与之前只有常数项的模型相比，这个常数加余弦函数的新模型显然更符潜在函数。另一方面，重要的是要记住，尽管数学模型存在于整个 $\mathsf{X}$ 轴上，但它仅适用于观察区间 (0-L) 内的物理问题，并且在该区间内，模型严格仅适用于实际测量的2个点。在间隔之外，模型是荒谬的，因为有充分的理由期望物理图像不是周期性的。即使在区间内，模型对于实际数据点之间的 $\mathsf{X}$ 值也可能没有意义。为了判断模型作为插值函数(interpolation function)的有用性，我们必须求助于我们对所研究的物理系统的理解。在后面的部分中，我们将扩展此示例以包含 D = 3 个样本，但在此之前，我们需要更深入地了解我们刚刚介绍的Fourier分析过程。

3.4 Fourier分析是一种线性变换

如前例所示，离散函数的Fourier分析产生的模型由正弦曲线的加权和加上一个常数组成。这些权重或傅立叶系数是模型的未知参数，必须根据数据确定。上例中用于产生系数值的计算方法是求解两个未知数的两个线性方程。这表明我们将方程 [3.3] 写成矩阵形式如下

$\begin{bmatrix} \mathsf{Y}_0\\ \mathsf{Y}_1 \end{bmatrix}=\begin{bmatrix} 1 \hspace{0.5cm}& cos(0) \\ 1 \hspace{0.5cm}& cos(\pi) \end{bmatrix}.\begin{bmatrix} m\\a \end{bmatrix}$ ---------------------------------------------------------[3.6]

当按这种方式书写的时候，Fourier分析就像第2章中描述的那种线性变换。即，假如我们将我们的两个采样点 $\mathsf{Y}_0$ 和 $\mathsf{Y}_1$ 看成是二维数据向量 v 的两个分量，则v显然是由Fourier系数 m 和 a 组成的某个其他向量 f 的变换。在矩阵记法中，声明是 v = M.f 。逆变换为 $f = M^{-1}.v$ ，表明Fourier系数向量 f 是已知数据向量 v 的一个线性变换。为了证明这一点，首先我们求得矩阵M的逆矩阵，然后用这个结果将向量 v 写成下式

$\begin{bmatrix} m\\a \end{bmatrix}=\frac{1}{2}.\begin{bmatrix} 1 \hspace{0.5cm}& 1 \\ cos(0) \hspace{0.5cm}& cos(\pi) \end{bmatrix}.\begin{bmatrix} \mathsf{Y}_0\\ \mathsf{Y}_1 \end{bmatrix}$ --------------------------------------[3.7]

显然，这等价于[3.4]，(公因子1/2 已经从这个逆矩阵 $M^{-1}$

的元素中提取出来了。) 在Fourier分析的语言中，等[3.7]描述为数据向量 v 到Fourier系数向量 f 的离散Fourier变换(Discrete Fourier Transform，简记为DFT)。反之，等式[3.6]描述为 f 的逆离散Fourier变换重现数据向量v 。

3.5 Fourier分析是一种基向量的变更

观察Fourier分析的另一种方式在于其自我暗示。如果我们重写等式[3.6]为向量和

$\mathsf{v} = ( \mathsf{Y}_0 , \mathsf{Y}_1 ) = (m + a.cos( 0 ), m + a.cos( \pi ))$

$= (m , m ) + a (cos( 0 ), cos( \pi ))$

$= m C_0 + a C_1$ ---------------------------------------------------------------------------------[3.8]

其中， $C_0$ 是给定采样点计算出来的常量函数 cos(0*2π / )， $C_1$ 是给定采样点计算出来的基本谐波函数 cos(1*2π / )，

$C_0 = (1,1)$

$C_1 = (cos( 0 ), cos( \pi )) = (1,-1)$ -------------------------------------------[3.9]

换言之，这些等式指的是，数据向量 v 是两个其它向量 $C_0$ 和 $C_1$ 的加权和。注意，向量 $C_0$ 和 $C_1$ 是正交的(译注：几何上表现起来就是垂直，代数上表现起来就是内积为0)，因此也是线性无关的，所以可以为二维向量空间用于表示v提供替代基向量。这种解释如图3.4所示。 以这种观点看待这个问题的优点在于，它提供了一种计算未知参数m的 a的几何解释。这些参数在基向量 $C_0$ 和 $C_1$ 方向表示 v 的分量。从第 2 章我们知道，这些分量是通过将 v 投影到基向量上而找到的，并且这些投影的长度可以通过内积来计算。因此，我们可通过按如下方式通过计算内积 $\mathsf{v}\bullet C_0$ 来求得 m ：

$\mathsf{v} \bullet C_0 = (m C_0 + a C_1)\bullet C_0$

$= m C_0 \bullet C_0 + a C_0 \bullet C_1$

$= m |C_0 |^2$ ------------------------------------------------------------------------------------------[3.10]

---------------------------图 3.4 Fourier分析视作一种基向量的变更------------------------------------------

注意[3.10]中的第二项消掉了，因为这两项具有正交性。重排这个等式，我们得到

$m = \frac{v \bullet C_0}{|C_0 |^2} = \frac{\mathsf{Y}_0+\mathsf{Y}_1}{2}$ -------------------------------------------------------[3.11]

类似地，我们可通过按如下方式通过计算内积 $\mathsf{v}\bullet C_1$ 来求得a：

$\mathsf{v} \bullet C_1 = C_1 (m C_0 + a C_1)$

$= m C_1 \bullet C_0 + a C_1 \bullet C_1$

$= m |C_1 |^2$ ---------------------------------------------------------------------------[3.12]

再次，因为第一项两向量的正交性，消除掉了，从而求得

$a = \frac{\mathsf{v} \bullet C_1}{|C_1 |^2} = \frac{\mathsf{Y}_0-\mathsf{Y}_1}{2}$ -------------------------------------------------------[3.13]

数据向量 v 与向量 $C_0$ 和 $C_1$ 的内积的重复形成表明了(有点非常规的)矩阵表示法

$\begin{bmatrix} m\\ a \end{bmatrix} = \frac{1}{2}\begin{bmatrix} C_0 \hspace{0.5cm} & \rightarrow \\ C_1 \hspace{0.5cm}& \rightarrow \end{bmatrix}.\begin{bmatrix} \mathsf{Y_0}\\ \mathsf{Y_1} \end{bmatrix}$ --------------------------------------------------[3.14]

上式与等式[3.7]一样，在等式中，C -> 表示包含余弦波采样点的行向量。

从这个讨论中得出的结论是，如果我们将函数两个采样序列表示为数据向量 v，那么，我们可以通过创建两个正交向量 $C_0$ 和 $C_1$ 并将数据向量投影到这两个新的基向量的方式，对这个数据向量进行Fourier分析。这些投影的长度可以解释为数据向量中存在的 $C_0$ 和 $C_1$ 的数量。由于 $C_0$ 只是采样常数函数，而 $C_1$ 是采样余弦函数，这些投影告诉我们数据中存在多少常数和多少余弦。这就是Fourier分析的全部意义所在！在下一节中，我们将扩展这条推理路径以处理 D = 3 个样本的情况，然后将结果推广到任意数量的样本。

3.6 在3点采样的函数

现在让我们回到测量图 3.2 的温度函数的问题。我们已经看到，如果我们在两个点对温度进行采样，那么具有两个项的Fourier级数将与这两个测量值完全吻合。为了概括这一观察，我们可能期望三个样本将完全符合 3 项Fourier级数，四个样本将符合 4 项Fourier级数，等等。“多少项足够？”这个显而易见的问题。稍后的章节会处理。目前，我们可以说两件事。首先，要用Fourier模型完美拟合连续函数，需要无限多的项。其次，我们可以想象，如果采样了足够多的点，即如果样本足够靠近，那么使用Fourier模型在点之间进行插值所产生的误差将变得微不足道。为了进一步明晰这种不确切的表述，我们需要定义“足够多点”所指以及模型的错误何时才“微不足道”的标准。然后，要判断一个特定模型是否满足这些标准，我们最终必须依赖于我们对问题物理学的理解。但在我们解决这些重要问题之前，我们需要开发适用于任意数量样本点的Fourier级数的通用公式。在我们考虑一个更具体的例子，即 D = 3 之后，我们将能够做到这一点。

为了获得图3.2中那样的潜在函数的更好的模型，假设测量值 $\mathsf{Y}_0$ , $\mathsf{Y}_1$ 和 $\mathsf{Y}_2$ 分别在三个深度 = 0 ， = /3 和 = 2/3处采样取得，如图3.5所示。这些值分别对应将整个区间划分成D = 3 等份后的3个子区间的开始。

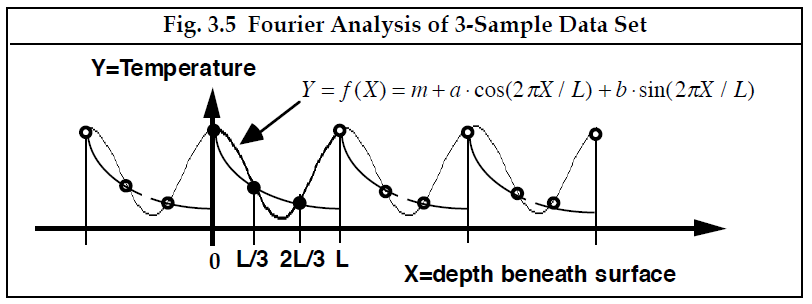
---------------------------图 3.5 3个采样黄河口的Fourier分析---------------------------------------------------

现在我们有了第三个测量值，我们可以向我们的三角模型添加第三项。因此，我们寻求用以下的Fourier级数来适配测量数据

$Y = f ( X ) = m + a.cos(2\pi \mathsf{X}/ \mathsf{L}) + b.sin(2\pi \mathsf{X}/ \mathsf{L})$ 。-------------[3.15]

为了确定3个未知的Fourier系数 m，a 和 b，我们以在三个值处测得的值来计算方程 [3.15]。结果是3个线性方程组

$\mathsf{Y}_0 = m + a.cos( 0 ) + b.sin( 0 )$ ..........................@ = 0

$\mathsf{Y}_1 = m + a.cos( 2\pi/3 ) + b.sin( 2\pi/3 )$ ..................@ = /2

$\mathsf{Y}_2 = m + a.cos( 4\pi/3 ) + b.sin( 4\pi/3 )$ ..................@ = /2 -----------[3.16 ]

为了解这个线性方程组，我们首先将它们写成 v = Mf 的矩阵形式如下

$\begin{bmatrix} \mathsf{Y}_0\\ \mathsf{Y}_1 \\\mathsf{Y}_2 \end{bmatrix} = \begin{bmatrix} 1\hspace{0.2cm}&cos(0)\hspace{0.2cm}&sin(0)\\ 1\hspace{0.2cm}&cos(2\pi/3)\hspace{0.2cm}&sin(2\pi/3)\\ 1\hspace{0.2cm}&cos(4\pi/3)\hspace{0.2cm}&sin(4\pi/3) \end{bmatrix}. \begin{bmatrix} m\\a \\b \end{bmatrix}$ ------------------------------[3.17]

当按这种方式书写的时候，矩阵 M 的列立即识别为构成我们的Fourier模型的基的采样三角函数的列向量 $C_0$ ， $C_1$ 和 $S_1$ 。这预示着更紧凑的记法(使用箭头表示矩阵中的列向量)

$\mathsf{v} =\begin{bmatrix} C_0 \hspace{0.2cm}&C_1 \hspace{0.2cm}&S_1 \\ \downarrow& \downarrow & \downarrow \end{bmatrix}\cdot f$ ----------------------------------------------------------------------------[3.18]

据此，推断出向量v 是基向量的加权和

$\mathsf{v} = m C_0 + a C_1 + b S_1$ 。----------------------------------------------------------------------[3.19]

换句话说，假如我们想象从3个给定的值构成一个3维数据向量，则这个向量存在于一个3维空间中，该空间由分布着一组可替代的基向量：采样三角函数。每个向量的数量可应用等式 3.18 计算所得，这种计算称为逆离散Fourier变换(inverse discrete Fourier transform，简记为IDFT)。

------------------------------图3.6 3个点的离散函数向量表示-----------------------------------------------------

因此，我们可以认为数据向量是这些基向量的加权和，相应的权重是我们想要的未知Fourier系数。这个问题的几何观点表明，为了确定Fourier系数，我们应该通过形成内积将数据向量依次投影到每个基向量上。例如，将 v 投影到 $C_0$ 给出

$\mathsf{v} \bullet C_0 = (m C_0 + a C_1 + b S_1) \bullet C_0$

$= m C_0\bullet C_0 + a C_1\bullet C_0 + b S_1\bullet C_0$

$= m C_0\bullet C_0$

$= m |C_0 |^2$ -----------------------------------------------------------------------[3.20]

注意，除了一项其它项都消减了，因为其正交性。从练习3.3我们可知， $C_0$ 的平方长度是D(Dimensionality)，即问题的维数(本例中为D = 3)。因此，第一个Fourier系数是

$m = \frac{\mathsf{v} \bullet C_0}{D}$ -----------------------------------------------------------------------[3.21]

按类似的推理路径，我们求得了另外两个Fourier系数

$a = \frac{\mathsf{v} \bullet C_1}{D/2}$

$b = \frac{\mathsf{v} \bullet S_1}{D/2}$ ---------------------------------------------------------------------------[3.22]

这最后两个等式可以结合起来给出矩阵形式(使用箭头表示矩阵中的行向量)

$\begin{bmatrix} m\\ a \\ b \end{bmatrix}= \begin{bmatrix} C_0/D\hspace{0.2cm}&\rightarrow\\ 2C_1/D\hspace{0.2cm}&\rightarrow \\ 2S_1/D\hspace{0.2cm}&\rightarrow \end{bmatrix}\bullet \begin{bmatrix} \mathsf{Y_0}\\ \mathsf{Y_1}\\ \mathsf{Y_2} \end{bmatrix}$ ------------------------------[3.23]

可以通过提取公因子 2/D 得到前向离散Fourier变换 (DFT) 来简化

$f=\frac{2}{D}\cdot \begin{bmatrix} C_0/2\hspace{0.2cm}&\rightarrow\\ C_1\hspace{0.2cm}&\rightarrow \\ S_1\hspace{0.2cm}&\rightarrow \end{bmatrix}\cdot \mathsf{v}$ ---------------------------------------------[3.24]

总之，等式 [3.16] 到 [3.19] 是表示 D = 3 情况下的逆 DFT 的不同方式。因此，他们告诉我们如何从Fourier系数“重建”测量数据点。但我们需要解决相反的问题：给定测量值，确定未的Fourier系数。换句话说，我们寻求前向DFT， $f=M^{-1}\cdot \mathsf{v}$ ，这意味着我们必须求得矩阵 M 的逆矩阵。我们的求解方法利用了正交性的优点，通过重复地组成数据向量与每个三角基向量的内积的方式求解。当每个内积除以相应基函数的长度时，其结果在几何上被解释为向量 v 在基向量上的投影的长度。这些长度等于模型中的Fourier系数。

3.7 在D点采样的函数

前面 D = 1、2 和 3 的示例指出了确定适用于任意点数的三角模型的Fourier系数的通用方法。在第 3.1 节中，我们推断，模型中所有三角函数元素的周期必须是观察区间的某个整数分数。即，周期一定等于 /k ,其中，是k一个整数，我们称之为谐波数(harmonic number)。因此，我们寻求的Fourier级数具有形式

$Y = f ( X ) = m + \sum_{k=1}^{N}[a_{k} cos(2\pi k \mathsf{X}/ \mathsf{L}) + b_k.sin(2\pi k \mathsf{X}/ \mathsf{L})]$

。---------------------------------------------------------[3.25]

假如我们对自变量做一点改变，以此稍微简化一下记法，或许更容易掌握

$Y = f ( X ) = m + \sum_{k=1}^{N}[a_{k} cos(2 k \theta) + b_k.sin(2 k \theta)]$ , $\theta=2\pi \mathsf{X}/\mathsf{L}$ -------------------------------------------------------------- ----------------[3.26]

其中，当 D是偶数的时候，D = 2N , 当 D是奇数的时候，D = 2N + 1 。和以前的思路一样，我们假设区间从 0 到划分成 D 等份，且值发生在每个这些区间的开始，因此， $\theta _j=2\pi (S+j\mathsf{L}/D)/\mathsf{L}$ 。

对于 D 个数据点，有 D 个待确定的未知Fourier系数。如果方程 [3.26] 在我们测量的每个值进行计算，那么结果是一个 D 线性方程组，当写成矩阵形式时，是

$\begin{bmatrix} \mathsf{Y_0}\\\mathsf{Y_1}\\\mathsf{Y_2} \\ \mathsf{Y_3} \\ \vdots \\ \mathsf{Y_D} \end{bmatrix} \begin{bmatrix} \mathsf{C_0}\hspace{0.2cm}&\mathsf{C_1}\hspace{0.2cm}&\mathsf{S_1}\hspace{0.2cm}&\ldots\hspace{0.2cm}&\mathsf{C_N}\hspace{0.2cm}&&\mathsf{S_N}\\\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&&\downarrow \\ \\ \\ \\ \\ \end{bmatrix}\cdot \begin{bmatrix} \mathsf{m}\\\mathsf{a_1}\\\mathsf{b_1} \\ \vdots \\ a_N \\ b_N \end{bmatrix}$ -------------------------------[3.27]

紧凑地写成 f 与列向量矩阵的内积

$\mathsf{v} = \begin{bmatrix} C_0\hspace{0.1cm}&C_1\hspace{0.1cm}&S_1\hspace{0.1cm}&\ldots\hspace{0.1cm}&C_N\hspace{0.1cm}&S_N\\ \downarrow&\downarrow&\downarrow&\downarrow&\downarrow&\downarrow \end{bmatrix}\cdot f$ --------------------------------------------[3.28]

等式[3.27]和[3.28]显示的是当 D是奇数时的逆离散Fourier变换(IDFT)。当是D是偶数的时候，矩阵中最后一列( $S_N$ )和最后的Fourier系数( $b_N$ )被忽略。

为了获得前向 DFT，我们将 D 数据点设想为 D 维空间中的向量，可以表示为三角基向量的加权和。对应的权重是未知Fourier系数，其计算方法为通过依次将数据向量投影到每个基向量上的方式计算内积而求得。例如，我们将 v 投影到 $C_k$

$v \bullet C_k = (mC_0 + a_1 C_1 + b_1 S_1 + a_2 C_2 + b_2 S_2 + ... + a_N C_N + b_N S_N ) \bullet C_k$

$= a_k C_k \bullet C_k$

$= a_{k} |C_k |^2$

$= a_{k} D/2$ ----------------------------------------------------------------------------------------[3.29]

请注意，由于正交性，扩展内积中除一项外的所有项都消失了。回顾练习3.3， $C_k$ 的平方长度等于 D/2 ，因此，第 k 项 Fourier余弦系数由简单公式

$a_k = \frac{2}{D} \mathsf{v} \bullet C_k$

$= \frac{2}{D} \sum_{j=0}^{D-1}[\mathsf{Y}_j cos(k\theta_j)]$ ............................. $\theta_j=2\pi\mathsf{X}_j/\mathsf{L}$

---------------------------------------------------------------------------------------[3.30]

给出。

同样，第 k 项 Fourier正弦系数由简单公式

$a_k = \frac{2}{D} \mathsf{v} \bullet C_k$

$= \frac{2}{D} \sum_{j=0}^{D-1}[\mathsf{Y}_j sin(k\theta_j)]$ ............................ $\theta_j=2\pi\mathsf{X}_j/\mathsf{L}$

---------------------------------------------------------------------------------------[3.31]

给出。

因此，最后两个等式定义了每个傅里叶系数，除了两个不包含因子 2 的特殊例外。缺少该因子的原因是相应基向量的平方长度是 D 而不是 D/2。一个特例是第一个Fourier系数 m，它是均值(mean value)，另一个特例是最后一个Fourier系数，当 D 是偶数时,它为 $C_N$ 。

注意，这些结果表明，可以在不考虑其他Fourier系数的情况下计算任何特定的Fourier系数。这是采样正弦波正交性的简化结果。这一结果的一个实际意义是，如果只对某些感兴趣，则没有必要计算模型的所有Fourier系数。 另一方面，如果要计算所有的Fourier系数，那么通过如下方式的矩阵乘法一次计算它们会很方便，即

$\begin{bmatrix} m\\a_1 \\ b_1 \\ \vdots \\ a_N \\ b_N \end{bmatrix} = \begin{bmatrix} C_0/D\hspace{0.2cm}&\rightarrow\\ 2C_1/D\hspace{0.2cm}&\rightarrow\\ 2S_1/D\hspace{0.2cm}&\rightarrow\\ \vdots\hspace{0.2cm}&\rightarrow\\ 2C_N/D\hspace{0.2cm}&\rightarrow\\ 2S_N/D\hspace{0.2cm}&\rightarrow\\ \end{bmatrix} \cdot \begin{bmatrix} \mathsf{Y}_0\\ \mathsf{Y}_1\\ \mathsf{Y}_2\\ \mathsf{Y}_3\\ \vdots\\ \mathsf{Y}_{2N+1} \end{bmatrix}$ -----------------------------------------[3.32]

提出公因式 2/ D 之后简化为

$f=\frac{2}{D}\cdot \begin{bmatrix} C_0/2 \hspace{0.2cm}&\rightarrow \\ C_1 \hspace{0.2cm}&\rightarrow \\ S_1 \hspace{0.2cm}&\rightarrow \\ \vdots \hspace{0.2cm}&\rightarrow \\ C_N \hspace{0.2cm}&\rightarrow \\ S_N \hspace{0.2cm}&\rightarrow \end{bmatrix}\cdot \mathsf{v}$ -----------------------------------------------------------------[3.33]

3.8 整理(tidying up)

虽然刚刚开发的一般方程有效，但有几个在美学上令人不悦的特征，这些特征掩盖了(obscure)Fourier分析的重要几何解释。首先，需要一个特殊的公式来计算平均系数 m(译注：没将其统一起来)。如果我们设置 k = 0，方程 [3.30] 生成的答案恰好是均值的两倍。即 $a_0=2m$ 。这表明我们只要改变模型中的变量，我们就不需要将常数项视为特例。随着变量的这种变化，模型变为

$Y = y ( X ) = \frac{a_0}{2} + \sum_{k=1}^{N}[a_{k} cos(k \theta) + b_k.sin(k \theta)]$ , $\theta=2\pi \mathsf{X}/\mathsf{L}$ ----------------[3.34]

这就是教科书中普遍引用的Fourier级数形式。

接下来，在等式 [3.33] 的矩阵顶部元素中有不协调的(unsightly)因子 2。这种不规则(anormaly)是由于除 $C_0$ 外所有三角基向量的平方长度为 D/2 ,而 $C_0$ 的平方长度是 D 。这表明，在等式[3.27]中用 $\frac{\sqrt{2}}{\sqrt{2}}$ 乘以 $C_0$ ，然后在分子中析出因数 $\sqrt{2}$ ，并将它归入 Fourier级数向量中的 $a_0$ 项，如下等式[3.35]所示

$\begin{bmatrix} \mathsf{Y_0}\\\mathsf{Y_1}\\\mathsf{Y_2} \\ \mathsf{Y_3} \\ \vdots \\ \mathsf{Y_{2N}} \end{bmatrix} =\begin{bmatrix} \frac{\mathsf{C_0}}{\sqrt{2}}\hspace{0.2cm}&\mathsf{C_1}\hspace{0.2cm}&\mathsf{S_1}\hspace{0.2cm}&\ldots\hspace{0.2cm}&\mathsf{C_N}\hspace{0.2cm}&\mathsf{S_N}\\\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow \\ \\ \\ \\ \\ \end{bmatrix}\cdot \begin{bmatrix} \frac{a_0}{\sqrt{2}}\\ \mathsf{a_1}\\\mathsf{b_1} \\ \vdots \\ a_N \\ b_N \end{bmatrix}$ ---------------------------------------[3.35]

由于现在三角矩阵中的每一列向量都具有长度 $\frac{D}{\sqrt{2}}$ ,我们提出这个公因子使得每一列向量都具有单位长度。为了保持等式的整洁性，我们首先定义以下的单位基向量

$c_0=\frac{C_0/\sqrt{2}}{\sqrt{D/2}}=\frac{C_0}{\sqrt{D}}$

$c_k=\frac{C_k}{\sqrt{D/2}}$

$s_k=\frac{S_k}{\sqrt{D/2}}$ -----------------------------------------------------------------------------------[3.36]

因此，等式[3.35]现在就变成了

$\begin{bmatrix} \mathsf{Y_0}\\\mathsf{Y_1}\\\mathsf{Y_2} \\ \mathsf{Y_3} \\ \vdots \\ \mathsf{Y_{2N}} \end{bmatrix} = \frac{D}{\sqrt{2}} \cdot \begin{bmatrix} C_0\hspace{0.2cm}&\mathsf{C_1}\hspace{0.2cm}&\mathsf{S_1}\hspace{0.2cm}&\ldots\hspace{0.2cm}&\mathsf{C_N}\hspace{0.2cm}&\mathsf{S_N}\\\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow\hspace{0.2cm}&\downarrow \\ \\ \\ \\ \\ \end{bmatrix}\cdot \begin{bmatrix} \frac{a_0}{\sqrt{2}}\\ \mathsf{a_1}\\\mathsf{b_1} \\ \vdots \\ a_N \\ b_N \end{bmatrix}$ -----------------------[3.37]

写成紧凑记法为

$\mathsf{v}=\frac{D}{\sqrt{2}}\begin{bmatrix} C_0 \hspace{0.2cm}& C_1 \hspace{0.2cm}& S_1 \hspace{0.2cm}& \ldots & C_N \hspace{0.2cm} & S_N\\ \downarrow& \downarrow& \downarrow& \downarrow& \downarrow& \downarrow \end{bmatrix}\cdot f$ ---------------------------------------[3.38]

(逆 DFT)

注意，请记住 f 的第一项，即Fourier系数向量，与之前的用法有个 $\sqrt{2}$ 的差异。另外，需指出，当 D 是偶数时，[3.37]中最后一项Fourier系数是 $\frac{a_N}{\sqrt{2}}$ 。

以等式[3.38]的形式表示逆DFT的一个主要优点是三角向量矩阵是标准正交的，这意味着逆矩阵只是转置。因此，我们可以通过检查立即写出正向 DFT：

$f=\sqrt{2/D} \cdot\begin{bmatrix} C_0 \hspace{0.2cm}& \rightarrow\\ C_1 \hspace{0.2cm}&\rightarrow \\ S_1 \hspace{0.2cm}&\rightarrow \\ \vdots \hspace{0.2cm}& \rightarrow\\ C_N \hspace{0.2cm}& \rightarrow\\ S_N \hspace{0.2cm}& \rightarrow \end{bmatrix}\cdot y$ -------------------------------------------[3.39]

(前向DFT)

对称的等式对 [3.38] 和 [3.39] 很容易在计算机上编程实现。

这种形式的 DFT 等式的第二个优点是它揭示了Fourier分析的基本几何结构的根本简洁性。由于三角向量矩阵是标准正交的，所以它被识别为旋转矩阵。换言之，数据向量 v 通过旋转和尺度变化(由等式 [3.39] 中的常数乘数 $\sqrt{2/D}$ 表示) 转换为Fourier向量 f 。很自然地，数据向量的长度应该是相同的，不管它是在哪个参考系中被计算。这个几何概念在下面被表述为Parseval定理，它也可以在物理上解释为能量守恒的表述。

3.9 Parseval[pá:zeifa:l]定理

为表示数据向量 v 的 D 维空间定义了两组正交基向量后，针对这两个坐标参考系计算 v 的长度以进行比较是大有裨益的。我们之前已经了解到 v 与自身的内积产生向量的平方长度。 然而，在这样的计算中我们必须小心，因为我们已经看到两个参考系的比例不同。确保这些比例因子被考虑到位的一种方法是——将数据向量表示为指向坐标参考系基准方向(cardinal directions)的单位向量的加权和。换句话说，令

$\mathsf{v} = \mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N$ -------------------------------------------------------------[3.40]

其中，单位基向量 $\mathsf{u}_k$ 对第一个参考坐标系的坐标除了k维之外的每一维都是坐标0 ,而对k维的坐标为1。例如，

$u_1 = (1,0,0,0,...,0)$

$u_2 = (0,1,0,0,...,0)$

$u_D = (1,0,0,0,...,1)$ -------------------------------------------------------------------------[3.41]

现在形成 v 与自身的内积很容易计算，因为许多项由于基向量的正交性而消失，而其余项包含因子 u•u，它是单位的，因为基向量是单位长度。因此我们有，

$|\mathsf{v}|^2 = \mathsf{v} \bullet \mathsf{v} = (\mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N)( \mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N)$

$= (\mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N). \mathsf{Y}_1 \mathsf{u}_1 +$

$= (\mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N). \mathsf{Y}_2 \mathsf{u}_2 +$

$= (\mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N). \mathsf{Y}_3 \mathsf{u}_3 +$

$\vdots$

$= (\mathsf{Y}_1 \mathsf{u}_1 + \mathsf{Y}_2 \mathsf{u}_2 + ... + \mathsf{Y}_D \mathsf{u}_N). \mathsf{Y}_D \mathsf{u}_D$

$= |\mathsf{Y}_1 |^2 \mathsf{u}_1 \bullet \mathsf{u}_1 + |\mathsf{Y}_2 |^2 \mathsf{u}_2 \bullet \mathsf{u}_2 + ... + |\mathsf{Y}_D |^2 \mathsf{u}_D \bullet \mathsf{u}_D$

$= \sum_{k=1}^{D}|\mathsf{Y}_k |^2$ ----------------------------------------------------------------------------[3.42]

这就是 D 维空间的Pythagoras定理。请注意，等式 [3.42] 的简化如此显著，因为由于单位基向量 $u_i$ 的正交性，扩展形式中的每一行都减少为单个项。

按类似的推理思路，我们求得

$|f|^2= \frac{a_0}{\sqrt{2}}\mathsf{u}_1 + \mathsf{a}_1 \mathsf{u}_2 + \mathsf{b}_1 \mathsf{u}_3 + \mathsf{a}_2 \mathsf{u}_4 + \mathsf{b}_2 \mathsf{u}_5 + ...$

$= \frac{\mathsf{a}_0}{\sqrt{2}} + (\mathsf{a}_1)^2 + (\mathsf{b}_1)^2 + (\mathsf{a}_2)^2 +(\mathsf{b}_2)^2 + ...$

$= \frac{\mathsf{a}_0^2}{2} + \sum_{k=1}^{N}(\mathsf{a}_k^2+\mathsf{b}_k^2)$ --------------------------------------------------------------[3.43]

现在，当 v 在由采样三角函数根据等式[3.38]定义的替代参考坐标系中表示时，如果我们重复上述过程。则结果是

$|\mathsf{v}|^2 = \mathsf{v} \bullet \mathsf{v}$

$= \sqrt{D/2} (\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N )\cdot$

$\sqrt{D/2} (\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N )$

$= \frac{D}{2} [(\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N )\cdot \frac{a_0}{\sqrt{2}}c_0+$

$(\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N ) \cdot a_{1}c_{1}+$

$(\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N ) \cdot b_{1}s_{1}+$

$\ldots$

$(\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N ) \cdot a_{N}c_{N}+$

$(\frac{a_0}{\sqrt{2}}c_0 + a_1 c_1 + b_1 s_1 + ... + a_N c_N + b_N s_N ) \cdot b_{N}s_{N}]$

$=\frac{D}{2}[(a_0^2)/2 c_0 \bullet c_0 + a_1^2 c_1 \bullet c_1 + b_1^2 s_1 \bullet s_1 + ... + a_N^2 c_N \bullet c_N + b_N^2 s_N \bullet s_N]$

$= \frac{D}{2}[ \frac{a_0^2}{2} +\sum_{k=1}^{N} (a_k^2+b_k^2)]$ -----------------------------------------------------------------[3.44]

将等式[3.43]和[3.44]的结果组合起来，我们就得到了下面的恒等式

$|\mathsf{v}|^2 = \sum_{k=1}^{D}\mathsf{Y}_k^{2} = \frac{D}{2}[\frac{a_0^{2}}{2} + \sum_{k=1}^{N}(a_k^2+b_k^2) = \frac{D}{2}|f|^2$ ------------------------[3.45]

这被称为Parseval定理。换言之，Parseval定理指出数据向量的长度可以在空间/时间域(第一个参考坐标系)或Fourier域(第二个参考坐标系)中计算。该定理的意义在于它建立了基于数据向量的平方长度的两个域之间的桥梁关系。在以后的章节中，我们将看到，向量的平方长度在许多物理场景下如何可能地被解释为信号中的能量数，以及平方Fourier系数如何可能地被解释为等价于Fourier级数模型项中项的能量数。 从这个意义上讲，Parseval 定理是一个能量守恒定理，因为它指的是，信号包含相同数量的能量，而不管该能量是在空间域/时间域，还是在Fourier域/频率域中计算的。

3.10 关联统计

Parseval 定理的另一种解释与统计有关。如果我们重新排列等式[3.45] 通过将常数项 ( $m=a_0/2$ ) 移到左侧，我们得到

$\frac{1}{D}\sum_{k=1}^{D}\mathsf{Y}_k^{2} - m^2 = \frac{1}{2}[\sum_{k=1}^{N}(a_k^2+b_k^2)]$ ------------------------------------------------------------[3.46]

现在，该等式的左侧被识别为正在建模的离散函数中值的方差(variance)(译注：各个数据与平均数之差的平方的和的平均数)，而等式的右侧是三角Fourier系数的振幅平方之和的一半。此外，由于Fourier系数的振幅平方与模型中的能量相关，该等式表明一组数据点的方差也可以被视为是信号中能量数。

一旦数据被视为 D 维空间中的向量，统计学的其他方面也呈现出几何视角。例如，一组值和相应的值之间的相关性由 Pearson[píəsən]相关系数定义为

$m=\frac{\sum_{j=1}^{D}(x_{j}-\overline{x})(y_{j}-\overline{y})}{\sqrt{{(x_{j}-\overline{x})}^{2}{(y_{j}-\overline{y})}^{2}}}$ -------------------------------------------------------------[3.47]

如果我们将 值的集合设想为一个向量 ，那么我们可以通过从 的每个分量中减去平均 值来“归一化(normalize)” ，以产生一个新的向量 '，如下所示

$\mathsf{x}=(\mathsf{x}_1 ,\mathsf{x}_2 ,...,\mathsf{x}_D)$

$\overline{\mathsf{x}} = \overline{\mathsf{x}} (1,1,...,1)$

$\mathsf{x}' = -\overline{\mathsf{x}}$ -------------------------------------------------------------------------------------------------[3.48]

如果我们对值执行相同的操作以生成归一化向量 '，则等式[3.47]分子被认为是 ' 和 ' 的内积。在类似的灵光一闪中，我们注意到这个等式的分母是这两个向量长度的乘积。简而言之，我们看到

$r = \frac{x'\bullet y'}{|x' |\bullet|y' |}$

$= cos{(\theta)}$ ------------------------------------------------------------------------------------------------[3.49]

换句话说，( , )数据值样本中两个变量之间的相关性等于D维空间中两个对应的归一化数据向量之间的夹角。在这种几何解释中，相关性是衡量两个数据向量在 D 维空间中指向同一方向的程度。如果向量正交，则数据不相关。

--------------图 3.7 两个数据集和之间统计相关性的图形描述 (说明了 D = 2 次测量的情况。两个测量值 $( \mathsf{x}_1 , \mathsf{x}_2 )$ 绘制为左上面板中的数据向量，两个测量值 $( \mathsf{y}_1 , \mathsf{y}_2 )$ 绘制在右上面板中。一对辅助轴 $( \mathsf{x}'_1 , \mathsf{x}'_2)$ 和 $( \mathsf{y}'_1 , \mathsf{y}'_2)$ 以样本均值为中心，以显示数据向量 $\mathsf{x}'_1 = \mathsf{x}-\mathsf{x}_{mean}$ 和 $\mathsf{y}'_1 = \mathsf{y}-\mathsf{y}_{mean}$ 。当两组辅助轴叠加时，如图所示，两个数据向量之间夹角 θ 的余弦值等于 Pearson 相关系数 r。) ---------------

类似的推理表明在上的最佳拟合线性回归(best-fitting linear regression)的斜率等于

$slope = r. (|\mathsf{y}'|)/(||\mathsf{x}'|)$

$= r. \frac{\mathsf{x}' \bullet \mathsf{x}'}{|\mathsf{x}'|^2}$ ----------------------------------------------------------------------------------------[3.50]

3.11 图像对比和复合光栅(Image Contrast and Compound Gratings)

一些物理量，如光强度，总是正的。在这种情况下，正弦变化总是伴随着一个附加常数，以防止数量变为负值。在光学中，光关于平均值的正弦变化的相对量称为“对比度(contrast)”，亮度 L 的正弦空间图案称为光栅(grating)。普遍接受的正弦光栅对比度定义是Michaelson[màikəlsən]公式

$C =\frac{L_{max}-L_{min}}{L_{max}+L_{min}}$ ------------------------------------------------------------------------------[3.51]

计算对比度所需的各种参数只需通过检查光栅即可获得。为了解与Fourier分析的联系，可将此Michaelson公式重写为

$C =\frac{(L_{max}-L_{min})/2}{(L_{max}+L_{min})/2}$

$= \frac{amplitude}{mean} = \frac{m}{L_0}$ ------------------------------------------------------------------------------[3.52]

因此，在Fourier项中，对比度正是幅度(amplitude) m 对均值亮度(luminance) $L_0$ 的比率。

计算离散光学图像对比度的一般方法是基于显示器中所有像素的亮度值的标准偏差(deviation)。将对比度的定义应用于正弦光栅的情况

$L(x) = L_0 + m \cdot cos(2\pi fx - \Phi)$ -----------------------------------------------------------[3.53]

我们调用 Parseval 定理得到

$\frac{1}{D}\sum_{j=1}^{D}L_{j}^{2} = L_0^2 + \frac{m^2}{2}$ --------------------------------------------------------------------------[3.54]

左边的数量是平方像素强度的平均值，也称为亮度分布的二阶矩(second moment)。重排等式[3.54] 我们发现

$\frac{\sqrt{2}}{L_0}\sqrt{\frac{1}{D}\sum_{j=1}^{D}L_{j}^{2} -L_0^2} = \frac{m}{L_0}$ ---------------------------------------------------------------[3.55]

$\sqrt{2}$ •(像素标准偏差)/(均值亮度) = Michaelson对比度。

回想一下，分布的方差等于二阶矩——一阶矩的平方，通过对等式 [3.54] 的两边取平方根并将每一边除以平均亮度，我们恢复Michaelson对比度。因此，我们得出结论，正弦光栅的对比度可以计算为像素亮度值的标准偏差，由平均亮度归一化。

如果 n 个不同谐波频率的光栅叠加产生复合光栅，则总和的亮度分布 $\mathsf{L(x)}$ 为

$L(x)=\sum_{k=1}^{N} (L_k+m_k cos(2\pi f_k x - \Phi_k))$

$=\sum_{k=1}^{N} L_k+\sum_{k=1}^{N}{m_k cos(2\pi f_k x - \Phi_k)}$

$=L_{mean}+\sum_{k=1}^{N}{m_k cos(2\pi f_k x - \Phi_k)}$ -------------------------------------------------[3.56]

第 k 个分量的Michaelson对比度 $C_k = m_k / L_k$ , 因此，它的幅度是 $m_k = C_k * L_k$

。平均亮度等于组成光栅的平均亮度之和，但是我们应该如何定义这个复合光栅的对比度呢？我们再次根据图像中所有像素的亮度值的标准偏差寻找一些度量，并求助于 Parseval 定理， $\sum_{j=1}^{D}L_{j}^{2} = D [L_{mean}^{2} + \frac{1}{2}\sum_{k=1}^{N}m_k^2 ]$ ---------------------------------------------------------[3.57]

重排等式[3.57]我们得到

$(\frac{1}{D}\sum_{j=1}^{D}L_{j}^{2})- L_{mean}^{2} = \frac{1}{2}\sum_{k=1}^{N}m_k^2$ ------------------------------------------------------[3.58]

左边是复合光栅像素亮度值的方差，右边是分量光栅幅值平方和的一半。

如果我们等式 [3.58] 的第 k 次谐波对比度的定义， $m_k = C_k * L_k$ ，则结果可以根据对比度向量 $C_k$ 和构成复合光栅 L() 的分量光栅的平均亮度 $L_k$ 来表示，

$Var(L(\mathsf{x})) = \frac{1}{2} \sum_{k=1}^{N}m_k^2 = \frac{1}{2} \sum_{k=1}^{N}(C_k L_k)^2$ ---------------------------------------[3.59]

该结果表明，与随机变量一样，当两个光栅加在一起得到复合光栅时，复合光栅的像素方差等于分量光栅的像素方差之和。对等式 [3.59] 的两边取平方根并除以平均亮度给出(在 Matlab 符号中)复合光栅对比度的简单公式，表示为像素值的归一化标准偏差，或作为分量幅度向量的范数，

$\frac{\sqrt{2} Stdev(L(x)))}{L_mean} = \frac{norm(C.*L)}{sum(L)}$ ---------------------------[3.60]

尽管通过执行上面的一维分析简化了问题，但结论也适用于任何方向的二维光栅。Matlab 程序“test_contrast.m”为由不同方向和空间频率的光栅制成的格子提供了图形演示。

3.12 闭合曲线形状的Fourier描述符(Fourier Descriptors of the Shape of a Closed Curve)

平面图形的轮廓形成一条闭合曲线，定义了图形和背景之间的边界。 Fourier分析可用于提供曲线形状的简洁描述(compact description)，以及从曲线上的样本点插值(interplolating)平滑边界(smooth boundary)的过程。这种方法在 John C. Russ(IEEE 出版社）的“图像处理手册(The Image Processing Handbook)”一书中和 Charles T. Zahn 和 Ralph Z. Roskies 的“Fourier Descriptors for Plane Closed Curves(平面闭合曲线的Fourier描述符)”一书中有简要描述，IEEE Transactions on Computers(计算机汇刊)， 21卷，第 3 期，1972 年 3 月第269-281页。

Fourier描述符方法的形状描述的关键思想是将对象的边界视为复平面中的曲线。曲线上的每个点都由一个复数或相量指定，实部沿轴绘制，虚部沿轴绘制。在这种方法中隐含的是复数 = + i 是某些参数化(parametric)参数(例如时间)的函数。因此，实部 ()和虚部 () 都是的函数，边界曲线描绘了这两个函数如何共同变化。

举一个简单的例子，如果 ()= a*cos() 和 ()= a*sin() 那么 = cos()+ i * sin()描述了一个在复平面上半径为a 的圆。如果实部和虚部的半径不同，则曲线变为方程描述的椭圆

()= a*cos(), ()= b*sin(), 和 ()= a cos()+ i * b * sin()。---------------[3.61]

其中，a 和 b 是半轴长度。

显然，这些方程是周期性的，因此通常将它们写成更通用的Fourier形式

(θ)= a*cos(θ), (θ)= b*sin(θ), 和 (θ)= a cos(θ)+ i * b * sin(θ)。------------[3.62]

其中，θ = 2πt/L ，L 是周期(即循迹一次路径所需的时间)且0 < θ < 2π 。图3.8所示。

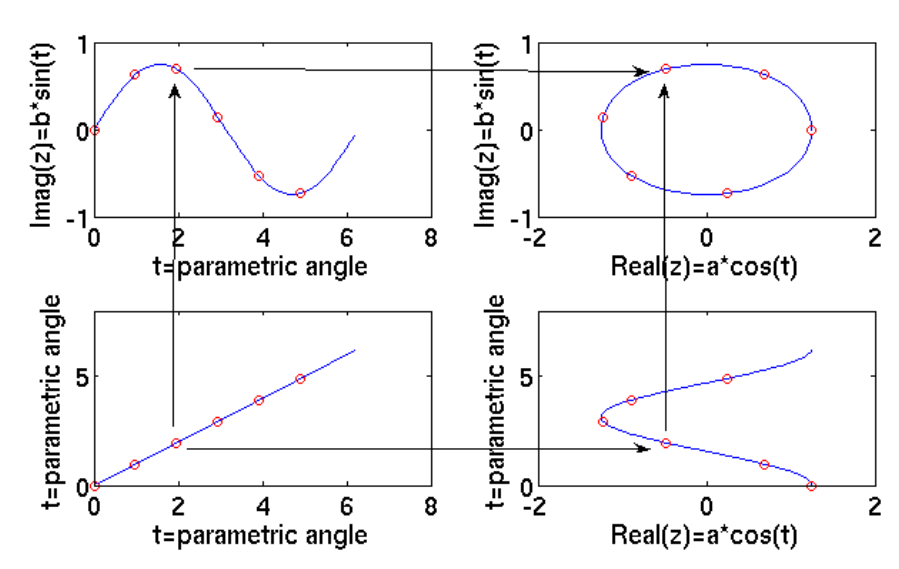
------------图 3.8复平面中椭圆的参数化生成。连续线显示完整曲线； 6 个等距点的子集用符号表示。箭头显示椭圆上的给定点与基础正弦曲线的关系-----------------

在这一点上很容易得出结论，参数角 θ 也是相量的相位角Φ，正如 Matlab 表达式Φ = angle() 所返回的那样。然而，事实并非如此。角度θ和 Φ 之间的关系如图 3.9 所示为 tan(Φ)/tan(θ) = b/a。

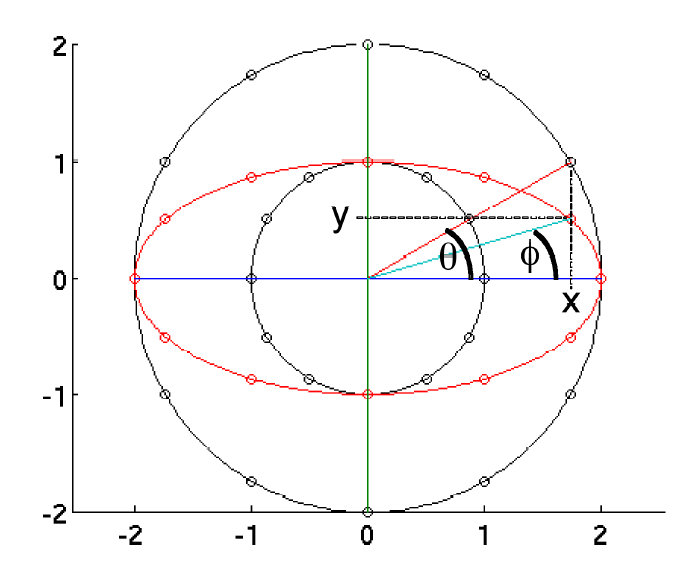
------------图 3.9 参数角θ与相量角 Φ 之间的关系。外圆的半径为a，内圆的半径为b，椭圆的长半径为a，短半径为b。椭圆上的点具有实部 = a*cos(θ) 和虚部 = b*sin(θ )。然而，其相位角 Φ 由 tan(Φ) = / = (b / a)*tan(θ) 给出。-----------------

这些观察的实际结果是椭圆的长轴(major axe)和短轴(minor axe)的知识对于从角度 Φ 推断角度 θ 是必要的。我们需要做出这种推断，因为离散曲线 (θ) 的Fourier分析假设我们知道样本点θ 。此外，要使用 Matlab 的标准 FFT 函数，我们需要样本角度在 0-2π周期内均匀分布。因此，实现椭圆或可能是任何其他曲线的Fourier描述的一个关键问题是——设计一种方法来推断沿对象边界的等距(equally spaced)样本角θ的向量。

在 Russ 的书中声称，等距采样点意味着复平面中采样点之间的距离相等。这相当于说样本点组成的多边形是等边的。然而，这与图 1 所示的结构不一致，因为图 1 中采样点之间的距离不均匀。这些点在长轴末端附近的间距比在短轴末端附近的间距更近。多边形也不是等角的，因为参数角在长轴端点附近比在短轴端点附近间隔更近。

鉴于上述观察，处理任意图形的第一步似乎必须是椭圆的拟合，以便可以估计半轴 a、b。同时，我们还需要估计长轴的角度倾斜，因为对于一般椭圆，椭圆的参数方程为：

(θ)= a cos(θ + 2α)+ i * b * sin(θ)。----------------------------------[3.63]

其中α是主轴与水平面的夹角。给定一个拟合椭圆，我们可以从等距参数角θ的向量计算出非等距相量角Φ的向量。然后使用此Φ向量将边界重新采样到一组相对较小的点上，这些点将平滑曲线表示为满足Fourier分析采样要求的多边形。

等式中 (θ) 的Fourier谱(spectrum)。(3.63) 在 Matlab 中计算为FFT()/length()。零频系数 $c_0$ 给出了图形质心(centroid)的坐标。正基频的系数 $c_{+1}$ 和负基频的系数 $c_{-1}$ 将长轴(a)、短轴(b) 和倾斜角 (α) 编码为一对复数。椭圆的参数可以从这些复值，即具有下列等式的基本Fourier系数中恢复，这些等式为

$a = |c_{(+1)}| + |c_{(-1)}|$ , $b = |c_{(+1)}| - |c_{(-1)}|$ , $\alpha = (angle(c_{(+1)})+ angle(c_{(-1)}))/2$ ---------------------------------------------[3.64]

综上所述，拟合椭圆的长轴长度 = 基本Fourier系数的大小之和；拟合椭圆的短轴长度 = 基本Fourier系数的大小差；拟合椭圆的倾斜度是两个系数相位角的平均值。高次谐波的系数调制椭圆以形成多边形的形状，并通过插值形成采样曲线的形状。

Fourier描述符的一种用途是量化图形既不是圆形也不是椭圆形的程度。纯圆形图形将由正基频处的单个Fourier系数来描述。纯椭圆形需要两个Fourier系数，分别对应正负基频。有很多方法可以描述椭圆图形偏离圆形的程度。受Fourier描述符启发的椭圆率指数是

椭圆率(Ellipticity) = $\frac{\sqrt{c_{+1}^2-c_{-1}^2}}{\sqrt{c_{+1}^2+c_{-1}^2}}=\frac{\sqrt{ab}}{\sqrt{(a^2+b^2)/2}}$ --------------------------------[3.65]

这个等式可以在几何上解释为两种估算椭圆平均半径的方法的比值。分子是长轴和短轴的几何平均数，等于 $\sqrt{(area/\pi)}$ (area表示面积) 。因此，它表示与椭圆面积相同的圆的半径。分母是长轴和短轴的 RMS(译注：Root Mean Square，均方根)，它等于沿外接矩形对角线的椭圆半径。对于圆，a = b 且椭圆度 = 1。

任何非椭圆形状的特征在于在高次谐波处存在非零Fourier描述符。一种量化偏离椭圆率的方法是受 Parseval 定理的启发，该定理指出信号中的总能量由Fourier系数的平方和给出。因此，高次谐波中的平方系数之和除以基频处的平方系数之和，是图形非椭圆度的大小不变和倾斜不变度量。

内容来源：

<< Fourier Analysis for Beginners>> Larry N. Thibos

你可能感兴趣的:(数学与应用数学,Fourier分析,离散函数,傅里叶,傅立叶)

斤斤计较的婚姻到底有多难？白心之岂必有为
很多人私聊我会问到在哪个人群当中斤斤计较的人最多？我都会回答他，一般婚姻出现问题的斤斤计较的人士会非常多，以我多年经验，在婚姻落的一塌糊涂的人当中，斤斤计较的人数占比在20～30%以上，也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中，有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型：第一种是物质上的，另一种是精神上的。在物质与精神上抠门已经严重的影响
QQ群采集助手，精准引流必备神器 2401_87347160 其他经验分享
功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具，它通过关键词搜索功能，帮助用户快速找到相关的微信群，并提供筛选是否需要验证的群组的功能。主要功能关键词搜索：用户可以输入关键词，工具将自动查找包含该关键词的微信群。筛选功能：工具提供筛选机制，用户可以选择是否只显示需要验证或不需要验证的群组。精准引流：通过上述功能，用户可以更精准地找到目标群组，进行有效的引流操作。3.设备需求该工具可以
机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
随笔 | 仙一般的灵气海思沧海
仙岛今天，我看了你全部，似乎已经进入你的世界我不知道，这是否是梦幻，还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求，这样才能够符合人生的梦想，生活才能够充满着阳光与快乐我不知道，我为什么会这样的感叹，是在感叹自己的人生，还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴，每天活在自己的梦中，活在一个不真实的世界是在逃避自己，还是在逃避周围的一切有时候我嘲笑自己，嘲笑自己如此的虚无，
一百九十四章. 自相矛盾巨木擎天
唉！就这么一夜，林子感觉就像过了很多天似的，先是回了阳间家里，遇到了那么多不可思议的事情儿。特别是小伙伴们，第二次与自己见面时，僵硬的表情和恐怖的气氛，让自己如坐针毡，打从心眼里难受！还有东子，他现在还好吗？有没有被人欺负？护城河里的小鱼小虾们，还都在吗？水不会真的干枯了吧？那对相亲相爱漂亮的太平鸟儿，还好吧！春天了，到了做窝、下蛋、喂养小鸟宝宝的时候了，希望它们都能够平安啊！虽然没有看见家人，也
element实现动态路由+面包屑软件技术NINI vue案例 vue.js 前端
el-breadcrumb是ElementUI组件库中的一个面包屑导航组件，它用于显示当前页面的路径，帮助用户快速理解和导航到应用的各个部分。在Vue.js项目中，如果你已经安装了ElementUI，就可以很方便地使用el-breadcrumb组件。以下是一个基本的使用示例：安装ElementUI（如果你还没有安装的话）:你可以通过npm或yarn来安装ElementUI。bash复制代码npmi
C语言宏函数南林yan C语言 c语言
一、什么是宏函数？通过宏定义的函数是宏函数。如下，编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
地推话术，如何应对地推过程中家长的拒绝校师学
相信校长们在做地推的时候经常遇到这种情况：市场专员反馈家长不接单，咨询师反馈难以邀约这些家长上门，校区地推疲软，招生难。为什么？仅从地推层面分析，一方面因为家长受到的信息轰炸越来越多，对信息越来越“免疫”；而另一方面地推人员的专业能力和营销话术没有提高，无法应对家长的拒绝，对有意向的家长也不知如何跟进，眼睁睁看着家长走远；对于家长的疑问，更不知道如何有技巧地回答，机会白白流失。由于回答没技巧和专业
C语言如何定义宏函数？小九格物 c语言
在C语言中，宏函数是通过预处理器定义的，它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为，但它们不是真正的函数，因为它们在编译时不会进行类型检查，也不会分配存储空间。宏函数的定义通常使用#define指令，后面跟着宏的名称和参数列表，以及宏展开后的代码。宏函数的定义方式：1.基本宏函数：这是最简单的宏函数形式，它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
微服务下功能权限与数据权限的设计与实现 nbsaas-boot 微服务 java 架构
在微服务架构下，系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加，如何保证不同用户和服务之间的访问权限准确、细粒度地控制，成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限：指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作，比如查看订单、创建订单、修改用户资料等。数据权限：
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
学点心理知识，呵护孩子健康静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
Long类型前后端数据不一致 igotyback 前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题，尤其是当后端使用Java的Long类型（64位）与前端JavaScript的Number类型（最大安全整数为2^53-1，即16位）进行数据交互时，很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
swagger访问路径 igotyback swagger
Swagger2.x版本访问地址：http://{ip}:{port}/{context-path}/swagger-ui.html{ip}是你的服务器IP地址。{port}是你的应用服务端口，通常为8080。{context-path}是你的应用上下文路径，如果应用部署在根路径下，则为空。Swagger3.x版本对于Swagger3.x版本（也称为OpenAPI3）访问地址：http://{ip
扫地机类清洁产品之直流无刷电机控制悟空胆好小清洁服务机器人单片机人工智能
扫地机类清洁产品之直流无刷电机控制1.1前言扫地机产品有很多的电机控制，滚刷电机1个，边刷电机1-2个，清水泵电机，风机一个，部分中高端产品支持抹布功能，也就是存在抹布盘电机，还有追觅科沃斯石头等边刷抬升电机，滚刷抬升电机等的，这些电机有直流有刷电机，直接无刷电机，步进电机，电磁阀，挪动泵等不同类型。电机的原理，驱动控制方式也不行。接下来一段时间的几个文章会作个专题分析分享。直流有刷电机会自动持续
店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码说私域人工智能小程序
摘要：本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合，阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇，提升了用户信任感、拓展了营销渠道，并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展，社区团购作为一种新兴的商业模式，在满足消费者日常需
2021-08-26 影幽
在生活中，女人与男人的感悟往往有所不同。人生最大的舞台就是生活，大幕随时都可能拉开，关键是你愿不愿意表演都无法躲避。在生活中，遇事不要急躁，不要急于下结论，尤其生气时不要做决断，要学会换位思考，大事化小小事化了，把复杂的事情尽量简单处理，千万不要把简单的事情复杂化。永远不要扭曲，别人善意，无药可救。昨天是张过期的支票，明天是张信用卡，只有今天才是现金，要善加利用！执着的攀登者不必去与别人比较自己的
高级编程--XML+socket练习题 masa010 java 开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人（1）使用dom4j将信息存入xml中（2）读取信息，并打印控制台（3）添加一个city节点与子节点（4）使用socketTCP协议编写服务端与客户端，客户端输入城市ID，服务器响应相应城市信息（5）使用socketTCP协议编写服务端与客户端，客户端要求用户输入city对象，服务端接收并使用dom4j
抖音乐买买怎么加入赚钱?赚钱方法是什么测评君高省
你会在抖音买东西吗?如果会，那么一定要免费注册一个乐买买，抖音直播间，橱窗，小视频里的小黄车买东西都可以返佣金!省下来都是自己的，分享还可以赚钱乐买买是好省旗下的抖音返佣平台，乐买买分析社交电商的价值，乐买买属于今年难得的副业项目风口机会，2019年错过做好省的搞钱的黄金时期，那么2022年千万别再错过乐买买至于我为何转到高省呢？当然是高省APP佣金更高，模式更好，终端用户不流失。【高省】是一个自
2018-07-23-催眠日作业-#不一样的31天#-66小鹿小鹿_33
预言日：人总是在逃避命运的路上，与之不期而遇。心理学上有个著名的名词，叫做自证预言；经济学上也有一个很著名的定律叫做，墨菲定律；在灵修派上，还有一个很著名的法则，叫做吸引力法则。这3个领域的词，虽然看起来不太一样，但是他们都在告诉人们一个现象：你越担心什么，就越有可能会发生什么。同样的道理，你越想得到什么，就应该要积极地去创造什么。无论是自证预言，墨菲定律还是吸引力法则，对人都有正反2个维度的影响
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录 leetcode 算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
每日一题——第九十题互联网打工人no1 C语言程序设计每日一练 c语言
题目：判断子串是否与主串匹配#include#include#include//////判断子串是否在主串中匹配//////主串///子串///boolisSubstring(constchar*str,constchar*substr){intlenstr=strlen(str);//计算主串的长度intlenSub=strlen(substr);//计算子串的长度//遍历主字符串，对每个可能得
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
每日一题——第八十四题互联网打工人no1 C语言程序设计每日一练 c语言
题目：编写函数1、输入10个职工的姓名和职工号2、按照职工由大到小顺序排列，姓名顺序也随之调整3、要求输入一个职工号，用折半查找法找出该职工的姓名#define_CRT_SECURE_NO_WARNINGS#include#include#defineMAX_EMPLOYEES10typedefstruct{intid;charname[50];}Empolyee;voidinputEmploye
《庄子.达生9》钱江潮369
【原文】孔子观于吕梁，县水三十仞，流沫四十里，鼋鼍鱼鳖之所不能游也。见一丈夫游之，以为有苦而欲死也，使弟子并流而拯之。数百步而出，被发行歌而游于塘下。孔子从而问焉，曰：“吾以子为鬼，察子则人也。请问，‘蹈水有道乎’”曰：“亡，吾无道。吾始乎故，长乎性，成乎命。与齐俱入，与汩偕出，从水之道而不为私焉。此吾所以蹈之也。”孔子曰：“何谓始乎故，长乎性，成乎命？”曰：“吾生于陵而安于陵，故也；长于水而安于
水泥质量纠纷案代理词徐宝峰律师
贵州领航建设有限公司诉贵州纳雍隆庆乌江水泥有限公司产品质量纠纷案代理词尊敬的审判长、审判员：贵州千里律师事务所接受被告贵州纳雍隆庆乌江水泥有限公司的委托，指派我担任其诉讼代理人，参加本案的诉讼活动。下面，我结合本案事实和相关法律规定发表如下代理意见，供合议庭评议案件时参考：原告应当举证证明其遭受的损失与被告生产的水泥质量的因果关系。首先水泥是一种粉状水硬性无机胶凝材料。加水搅拌后成浆体，能在空气中
腾讯云技术深度探索：构建高效云原生微服务架构我的运维人生云原生架构腾讯云运维开发技术共享
腾讯云技术深度探索：构建高效云原生微服务架构在当今快速发展的技术环境中，云原生技术已成为企业数字化转型的关键驱动力。腾讯云作为行业领先的云服务提供商，不断推出创新的产品和技术，助力企业构建高效、可扩展的云原生微服务架构。本文将深入探讨腾讯云在微服务领域的最新进展，并通过一个实际案例展示如何在腾讯云平台上构建云原生应用。腾讯云微服务架构概览腾讯云微服务架构基于云原生理念，旨在帮助企业快速实现应用的容
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
jsonp 常用util方法 hw1287789687 jsonp jsonp常用方法 jsonp callback
jsonp 常用java方法 (1)以jsonp的形式返回:函数名(json字符串) /*** * 用于jsonp调用 * @param map : 用于构造json数据 * @param callback : 回调的javascript方法名 * @param filters : <code>SimpleBeanPropertyFilter theFilt
多线程场景 alafqq 多线程
0 能不能简单描述一下你在java web开发中需要用到多线程编程的场景？0 对多线程有些了解，但是不太清楚具体的应用场景，能简单说一下你遇到的多线程编程的场景吗？ Java多线程 2012年11月23日 15:41 Young9007 Young9007 4 0 0 4 Comment添加评论关注(2) 3个答案按时间排序按投票排序 0 0 最典型的如： 1、
Maven学习——修改Maven的本地仓库路径 Kai_Ge maven
安装Maven后我们会在用户目录下发现.m2 文件夹。默认情况下，该文件夹下放置了Maven本地仓库.m2/repository。所有的Maven构件(artifact)都被存储到该仓库中，以方便重用。但是windows用户的操作系统都安装在C盘，把Maven仓库放到C盘是很危险的，为此我们需要修改Maven的本地仓库路径。
placeholder的浏览器兼容 120153216 placeholder
【前言】自从html5引入placeholder后，问题就来了，不支持html5的浏览器也先有这样的效果，各种兼容，之前考虑，今天测试人员逮住不放，想了个解决办法，看样子还行，记录一下。【原理】不使用placeholder，而是模拟placeholder的效果，大概就是用focus和focusout效果。【代码】 <scrip
debian_用iso文件创建本地apt源 2002wmj Debian
1.将N个debian-506-amd64-DVD-N.iso存放于本地或其他媒介内，本例是放在本机/iso/目录下 2.创建N个挂载点目录如下： debian:~#mkdir –r /media/dvd1 debian:~#mkdir –r /media/dvd2 debian:~#mkdir –r /media/dvd3 …. debian:~#mkdir –r /media
SQLSERVER耗时最长的SQL 357029540 SQL Server
对于DBA来说，经常要知道存储过程的某些信息： 1. 执行了多少次 2. 执行的执行计划如何 3. 执行的平均读写如何 4. 执行平均需要多少时间列名 &
com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 7454103 eclipse
今天eclipse突然报了com/genuitec/eclipse/j2eedt/core/J2EEProjectUtil 错误，并且工程文件打不开了，在网上找了一下资料，然后按照方法操作了一遍，好了，解决方法如下：错误提示信息： An error has occurred.See error log for more details. Reason: com/genuitec/
用正则删除文本中的html标签 adminjun java html 正则表达式去掉html标签
使用文本编辑器录入文章存入数据中的文本是HTML标签格式，由于业务需要对HTML标签进行去除只保留纯净的文本内容，于是乎Java实现自动过滤。如下： public static String Html2Text(String inputString) { String htmlStr = inputString; // 含html标签的字符串 String textSt
嵌入式系统设计中常用总线和接口 aijuans linux 基础
嵌入式系统设计中常用总线和接口任何一个微处理器都要与一定数量的部件和外围设备连接，但如果将各部件和每一种外围设备都分别用一组线路与CPU直接连接，那么连线
Java函数调用方式——按值传递 ayaoxinchao java 按值传递对象基础数据类型
Java使用按值传递的函数调用方式，这往往使我感到迷惑。因为在基础数据类型和对象的传递上，我就会纠结于到底是按值传递，还是按引用传递。其实经过学习，Java在任何地方，都一直发挥着按值传递的本色。首先，让我们看一看基础数据类型是如何按值传递的。 public static void main(String[] args) { int a = 2;
ios音量线性下降 bewithme ios音量
直接上代码吧 //second 几秒内下降为0 - (void)reduceVolume:(int)second { KGVoicePlayer *player = [KGVoicePlayer defaultPlayer]; if (!_flag) { _tempVolume = player.volume;
与其怨它不如爱它 bijian1013 选择理想职业规划
抱怨工作是年轻人的常态，但爱工作才是积极的心态，与其怨它不如爱它。一般来说，在公司干了一两年后，不少年轻人容易产生怨言，除了具体的埋怨公司“扭门”，埋怨上司无能以外，也有许多人是因为根本不爱自已的那份工作，工作完全成了谋生的手段，跟自已的性格、专业、爱好都相差甚远。
一边时间不够用一边浪费时间 bingyingao 工作时间浪费
一方面感觉时间严重不够用，另一方面又在不停的浪费时间。每一个周末，晚上熬夜看电影到凌晨一点，早上起不来一直睡到10点钟，10点钟起床，吃饭后玩手机到下午一点。精神还是很差，下午像一直野鬼在城市里晃荡。为何不尝试晚上10点钟就睡，早上7点就起，时间完全是一样的，把看电影的时间换到早上，精神好，气色好，一天好状态。控制让自己周末早睡早起，你就成功了一半。有多少个工作
【Scala八】Scala核心二：隐式转换 bit1129 scala
Implicits work like this: if you call a method on a Scala object, and the Scala compiler does not see a definition for that method in the class definition for that object, the compiler will try to con
sudoku slover in Haskell (2) bookjovi haskell sudoku
继续精简haskell版的sudoku程序，稍微改了一下，这次用了8行，同时性能也提高了很多，对每个空格的所有解不是通过尝试算出来的，而是直接得出。 board = [0,3,4,1,7,0,5,0,0, 0,6,0,0,0,8,3,0,1, 7,0,0,3,0,0,0,0,6, 5,0,0,6,4,0,8,0,7,
Java-Collections Framework学习与总结-HashSet和LinkedHashSet BrokenDreams linkedhashset
本篇总结一下两个常用的集合类HashSet和LinkedHashSet。它们都实现了相同接口java.util.Set。Set表示一种元素无序且不可重复的集合；之前总结过的java.util.List表示一种元素可重复且有序
读《研磨设计模式》-代码笔记-备忘录模式-Memento bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ import java.util.ArrayList; import java.util.List; /* * 备忘录模式的功能是，在不破坏封装性的前提下，捕获一个对象的内部状态，并在对象之外保存这个状态，为以后的状态恢复作“备忘”
《RAW格式照片处理专业技法》笔记 cherishLC PS
注意，这不是教程！仅记录楼主之前不太了解的一、色彩（空间）管理作者建议采用ProRGB（色域最广），但camera raw中设为ProRGB，而PS中则在ProRGB的基础上，将gamma值设为了1.8（更符合人眼）注意：bridge、camera raw怎么设置显示、输出的颜色都是正确的（会读取文件内的颜色配置文件），但用PS输出jpg文件时，必须先用Edit->conv
使用 Git 下载 Spring 源码编译 for Eclipse crabdave eclipse
使用 Git 下载 Spring 源码编译 for Eclipse 1、安装gradle，下载 http://www.gradle.org/downloads 配置环境变量GRADLE_HOME，配置PATH %GRADLE_HOME%/bin，cmd，gradle -v 2、spring4 用jdk8 下载 https://jdk8.java.
mysql连接拒绝问题 daizj mysql 登录权限
mysql中在其它机器连接mysql服务器时报错问题汇总一、[running][email protected]:~$mysql -uroot -h 192.168.9.108 -p //带-p参数，在下一步进行密码输入 Enter password: //无字符串输入 ERROR 1045 (28000): Access
Google Chrome 为何打压 H.264 dsjt apple html5 chrome Google
Google 今天在 Chromium 官方博客宣布由于 H.264 编解码器并非开放标准，Chrome 将在几个月后正式停止对 H.264 视频解码的支持，全面采用开放的 WebM 和 Theora 格式。 Google 在博客上表示，自从 WebM 视频编解码器推出以后，在性能、厂商支持以及独立性方面已经取得了很大的进步，为了与 Chromium 现有支持的編解码器保持一致，Chrome
yii 获取控制器名和方法名 dcj3sjt126com yii framework
1. 获取控制器名在控制器中获取控制器名: $name = $this->getId(); 在视图中获取控制器名: $name = Yii::app()->controller->id; 2. 获取动作名在控制器beforeAction()回调函数中获取动作名: $name =
Android知识总结（二） come_for_dream android
明天要考试了，速速总结如下 1、Activity的启动模式 standard：每次调用Activity的时候都创建一个（可以有多个相同的实例，也允许多个相同Activity叠加。） singleTop：可以有多个实例，但是不允许多个相同Activity叠加。即，如果Ac
高洛峰收徒第二期：寻找未来的“技术大牛” ——折腾一年，奖励20万元 gcq511120594 工作项目管理
高洛峰，兄弟连IT教育合伙人、猿代码创始人、PHP培训第一人、《细说PHP》作者、软件开发工程师、《IT峰播》主创人、PHP讲师的鼻祖！首期现在的进程刚刚过半，徒弟们真的很棒，人品都没的说，团结互助，学习刻苦，工作认真积极，灵活上进。我几乎会把他们全部留下来，现在已有一多半安排了实际的工作，并取得了很好的成绩。等他们出徒之日，凭他们的能力一定能够拿到高薪，而且我还承诺过一个徒弟，当他拿到大学毕
linux expect heipark expect
1. 创建、编辑文件go.sh #!/usr/bin/expect spawn sudo su admin expect "*password*" { send "13456\r\n" } interact 2. 设置权限 chmod u+x go.sh 3.
Spring4.1新特性——静态资源处理增强 jinnianshilongnian spring 4.1
目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
idea ubuntuxia 乱码 liyonghui160com
1.首先需要在windows字体目录下或者其它地方找到simsun.ttf 这个字体文件。 2.在ubuntu 下可以执行下面操作安装该字体： sudo mkdir /usr/share/fonts/truetype/simsun sudo cp simsun.ttf /usr/share/fonts/truetype/simsun fc-cache -f -v
改良程序的11技巧 pda158 技巧
有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点，程序你只写一次，但以后会无数次的阅读。当你第二天回头来看你的代码时，你就要开始阅读它了。当你把代码拿给其他人看时，他必须阅读你的代码。因此，在编写时多花一点时间，你会在阅读它时节省大量的时间。让我们看一些基本的编程技巧：尽量保持方法简短永远永远不要把同一个变量用于多个不同的
300个涵盖IT各方面的免费资源（下）——工作与学习篇 shoothao 创业免费资源学习课程远程工作
工作与生产效率: A. 背景声音 Noisli:背景噪音与颜色生成器。 Noizio:环境声均衡器。 Defonic:世界上任何的声响都可混合成美丽的旋律。 Designers.mx:设计者为设计者所准备的播放列表。 Coffitivity:这里的声音就像咖啡馆里放的一样。 B. 避免注意力分散 Self Co
深入浅出RPC uule rpc
深入浅出RPC-浅出篇深入浅出RPC-深入篇 RPC Remote Procedure Call Protocol 远程过程调用协议它是一种通过网络从远程计算机程序上请求服务，而不需要了解底层网络技术的协议。RPC协议假定某些传输协议的存在，如TCP或UDP，为通信程序之间携带信息数据。在OSI网络通信模型中，RPC跨越了传输层和应用层。RPC使得开发

Fourier分析入门——第3章——离散函数的Fourier分析

第 3 章 离散函数的Fourier分析

3.1 引言

3.2 在1点采样的函数

3.3 在2点采样的函数

3.4 Fourier分析是一种线性变换

3.5 Fourier分析是一种基向量的变更

3.6 在3点采样的函数

3.7 在D点采样的函数

3.8 整理(tidying up)

3.9 Parseval[pá:zeifa:l]定理

3.10 关联统计

3.11 图像对比和复合光栅(Image Contrast and Compound Gratings)

3.12 闭合曲线形状的Fourier描述符(Fourier Descriptors of the Shape of a Closed Curve)

你可能感兴趣的:(数学与应用数学,Fourier分析,离散函数,傅里叶,傅立叶)

第 3 章离散函数的Fourier分析