Fourier分析入门——第7章——采样理论
目录
第 7 章 采样定理
7.1 引言
7.2 采样定理
7.3 错误识别(aliasing)
7.4 Parseval定理(Parseval[pázeifa:l])
7.5 截断Fourier级数和回归理论(Truncated Fourier Series & Regression Theory)
第 7 章 采样定理
7.1 引言
在第 6 章中,我们发现有限区间内的离散函数和连续函数的Fourier分析在概念上几乎没有区别。两种类型的函数都有离散谱,唯一的区别是离散函数具有有限数量的谐波分量(图 5.1 中的情况 1),而连续函数原则上具有无限数量的谐波(图 5.1 中的情况 3)。 然而,作业集中出现了一个奇怪的结果 #6 。在一个问题 (6.1) 中,发现连续函数的频谱和该函数的采样版本明显不同,而在另一个问题 (6.2) 中,两个频谱在谐波范围内完全相同 是可以比较的。这表明在某些情况下,函数完全由有限数量的样本决定。在本章中,我们探讨了获得该结果的条件。
7.2 采样定理
通常,定义在有限区间上的连续函数可以表示成第6章所展示的那样的有限项的Fourier级数
![]() -----------------------------[6.1]
-----------------------------[6.1]
然而,对于某些函数,对于大于某个值 W 的所有频率,Fourier系数可能全部为零。对于这样的频谱,我们可以将 W 视为频谱的带宽(bandwidth)。请注意术语带宽的先前用法与本次用法之间的细微差别。在讨论具有有限频谱的离散函数时,我们使用术语带宽来表示频谱中定义的最高频率。在这种情况下,W = D/2L。该定义意味着所有连续函数都具有无限带宽,因为 D = ∞。如果所有Fourier系数的幅度在某个极限频率 W 之外都为零,则另一种定义允许连续函数具有有限带宽。对于实际目的,这是一个更有用的定义,因此通常使用的术语带宽指的就是这种意义上的带宽。
现在考虑具有有限带宽的连续函数的结果。 图 7.1 显示了一个示例,其中只有常数项和前三个谐波的频谱不为零。现在想象一下试图从这个频谱“重建”空间/时间函数。在这方面我们有两种选择。首先,我们可以假设所有高于 W 的频率都不存在,在这种情况下,IDFT 运算将产生一个离散函数,如图 7.1 左侧的实心点所示。另一方面,我们可以使用整个为无限数量的谐波定义的频谱,在这种情况下,Fourier级数将产生图中所示的连续函数。现在我们断言重构的连续函数必须通过所示的离散点。这是成立的,因为虽然高次谐波已被接纳,但它们没有贡献,因为所有系数都为零。因此,在重构的过程中是否包含大于W 的谐波并不重要。唯一的区别是,当定义了无限数量的系数并给定值为零时,可以在每个 x 值而不是仅对应于 ![]() 的倍数的 x 值处合理地计算原始函数。
的倍数的 x 值处合理地计算原始函数。
-----------------------------------------------图 7.1 有限带宽的频率谱---------------------------------------------
我们可以通过令 ![]() 为由
为由
![]() (
( ![]() ,j =整数)-------------[7.1]
,j =整数)-------------[7.1]
定义的离散函数,并令g(x)为由
![]() (所有x )------------------------------------------------------------------[7.2]
(所有x )------------------------------------------------------------------[7.2]
定义的连续函数, 将前面的论证,置于一个量化的基础上(a quantitative footing)。因为[7.1]和[7.2]的右边是相等的,可以推导出,对于采样点 ![]() , f ( x ) = g( x ) ,对于所有其它 x 值而言,g( x ) 插值(interpolates) f ( x ) (译注:使连续曲线 g( x ) 通过全部离散数据点,或使全部离散数据点适配连续函数 g( x ) )。
, f ( x ) = g( x ) ,对于所有其它 x 值而言,g( x ) 插值(interpolates) f ( x ) (译注:使连续曲线 g( x ) 通过全部离散数据点,或使全部离散数据点适配连续函数 g( x ) )。
前面的讨论表明,连续函数 g( x ) 是离散函数 f ( x ) 的合理插值。 持怀疑态度的学生可能仍然不相信这是正确的插值。为了说服,假设我们从连续函数 g( x ) 开始,我们预先知道它的频带限制为 W 。据此信息,则我们对 g( x ) 进行采样以生成离散函数 f ( x )。上述论点表明,如果我们以 R = 2W 的速率采样,则对于所有小于 W 的频率,f ( x ) 的频谱将与 g( x ) 的频谱相同。因此,g( x ) 的频谱可以通过添加无限数量的高次谐波从计算 f ( x ) 和频谱中导出,所有高次谐波的振幅均为零。这种用零填充频谱的策略被广泛用于提高 具有IDFT功能的重构函数空间分辨率的数值方法。 由于这个合成光谱将准确地重建 g( x ),因此我们得出结论:
精确地在有限区间内重建带限函数所需的所有信息都包含在有限数量的样本中。如果 采样率 R 超过 2W,其中 W 是给定函数的带宽;并且采样过程没有错误,则重建将没有错误。
这就是著名的采样定理,Whittaker[hwítikə](1935)在插值理论的背景下发展了该定理, 而Shannon[ʃǽnən](1949) 在信息论的背景下发展了该定理。Bergmann[bə:gmən] (1858) 在视网膜图像(retinal image)的神经采样(neural simpling)的背景下发现了这个思想,这是一个历史性的疏忽(oversight),后来 Helmholtz[hélmhoults](1867)在他被广泛引用的规则中推广了这个思想,即视觉分辨率要求在两个相对未受刺激的神经元(unstimulated neuron)之间至少需要一个相对的未受刺激神经元(即每个视觉模式周期至少有 2个神经样本)。 这条规则随后在 1930 年代被贝尔电话实验室的通信工程师 Nyquist[ˈnaɪ.kwɪst]重新发现。
7.3 错误识别(aliasing)
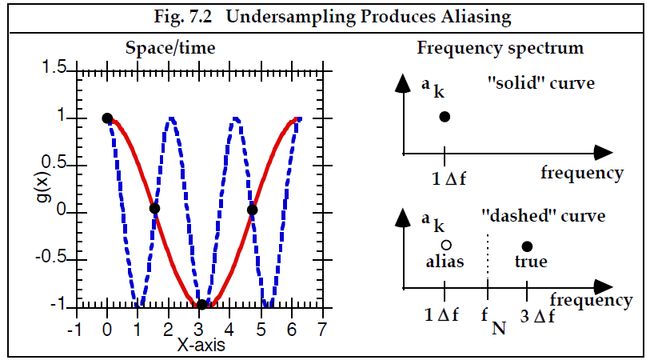
假如采样定理所要求的条件 R > 2W未被满足,则在函数重建的过程中将会引发错误。当由于欠采样(undersampling)而引发错误的时候,就称发生了错误识别(aliasing)。这个词“错误识别”用于这种背景下,是因为当采样率过低的时候,高频分量被误作(或伪装成(masquerades))低频分量。如图 7.2所示的一个例子,对区间上 D = 4的采样。因此,根据采样定理,可充分采样的最高频率(译注:指的是被采的频谱的频率)为 ΔfD/2,在本例中为 2Δf 。这个临界频率称为Nyquist频率,在图中用 fN 表示。由于实曲线具有低于临界频率的频率,因此它满足采样定理要求并且可以从频谱忠实地重建。
--------------------------------------------------图 7.2 欠采样产生错误识别-----------------------------------------
然而,虚线曲线的频率高于Nyquist频率,因此是欠采样的。欠采样虚曲线的频谱将与实曲线的频谱相同,因为这两个函数在样本点处相等。因此,虚线曲线似乎具有由标记为“错误识别”的空心圆圈所示的频谱。 虽然我们还不能证明这一说法,但事实证明,可以通过反映关于临界Nyquist频率的真实频谱,从真实频谱中预测欠采样函数的频谱。因此,Nyquist频率有时被称为“折叠频率”。我们将在第 13 章回到这个问题。
7.4 Parseval定理(Parseval[pázeifa:l])
在第 3 章中,我们介绍了离散函数的 Parseval 定理。承诺在以后的章节中我们将看到如何将 Parseval定理解释为一种能量守恒定理,该定理表示信号包含给定量的能量,而不管该能量是在空间/时间域还是在Fourier/频域中计算的。我们现在能够迎接这一挑战。
在第 5 章中,我们注意到连续函数与其自身的内积在许多物理情况下具有重要的解释,即信号中的总能量
![]() 数据函数的长度平方---------------------[5.8]
数据函数的长度平方---------------------[5.8]
假如我们将v(t) 替换为相应的Fourier级数,并选一个方便的观察区间(0,2π)以简化记法,我们求得无限级数
![]()
![]()
![]()
![]()
![]() --------------------------------------------------------------------------------------------------------------[7.3]
--------------------------------------------------------------------------------------------------------------[7.3]
积分的线性属性意味着和的积分是积分的和。由于正交性,这个无限系列的积分(每个积分在被积函数中都有无限数量的项)可以缩减为一个可管理的结果。
![]()
![]()
![]()
![]() ---------------------------------------------------------------------------------------------------------------[7.4]
---------------------------------------------------------------------------------------------------------------[7.4]
我们先前求得(等式[5.5]) ![]() 或
或 ![]() 在区间(0,2π)上的积分等于π 。因此,等式[7.4]简化为
在区间(0,2π)上的积分等于π 。因此,等式[7.4]简化为
![]() ------------------------------------------------------------------------[7.5]
------------------------------------------------------------------------[7.5]
将等式[5.7]和[7.5]结合在一起,我们得到连续函数的Parseval定理。
![]()
![]()
![]()
![]()
= ![]() { Fourier向量能量的平方 }--------------------------------------------------------------------------------[7.6]
{ Fourier向量能量的平方 }--------------------------------------------------------------------------------[7.6]
因此,Parseval 定理告诉我们,总功率等于均值的平方加上正弦Fourier分量幅值平方和的一半,即Fourier系数向量的平方长度的一半。但是,任何给定Fourier分量的幅度平方的一半就是该分量的功率。 因此,总功率是每个Fourier分量的功率之和。 通常,均值 (DC,Direct Current)(译注:直流) 项并不重要,因为信息仅由信号关于均值的变化(例如视觉刺激的空间或时间对比度)携带。 在这种情况下,我们可以说信号功率等于Fourier分量的平方幅度之和的一半,这也是信号均值为零时信号的方差。虽然理论要求Fourier相量的长度是无限的,但任何物理信号总是带限的,因此功率是有限的。
7.5 截断Fourier级数和回归理论(Truncated Fourier Series & Regression Theory)
为了进行稍微不同的推理,假设给定了一个定义在区间 (-π,π)上的函数 f ( x )。我们知道 f ( x )正好等于无限Fourier级数
![]() ----------------------------------------------------[7.7]
----------------------------------------------------[7.7]
然而,我们希望通过带宽限于 M 次谐波的有限Fourier级数带来逼近 f ( x )。 也就是说,我们试图通过截断的Fourier级数 g ( x )
![]() ----------------------------------------------------[7.8]
----------------------------------------------------[7.8]
来逼近 f ( x )。
在回归统计理论(statistical theory of regression)中,近似值的“拟合优度(goodness of fit)”通常用“均方误差(mean squared error)”(译注:差的平方再取平均)来衡量。通过该度量,上述逼近的误差可以通过定义为的均方误差 ε 来量化,定义为
![]()
![]() ---------------------------------[7.9]
---------------------------------[7.9]
根据 Parseval 定理,我们将 [7.9] 中的第一个积分解释为数据函数中的功率,第三个积分是Fourier级数模型中的功率。中间项是模型与给定函数的内积。
现在的目标是找出什么Fourier系数 ![]() 和
和 ![]() 的值会使ε最小。要了解答案的结果,请考虑 M = 1 的最简单情况。也就是说,我们希望通过函数
的值会使ε最小。要了解答案的结果,请考虑 M = 1 的最简单情况。也就是说,我们希望通过函数 ![]() 来逼近 f ( x )。 在这种情况下,错误是
来逼近 f ( x )。 在这种情况下,错误是
![]()
= f ( x )中的功率 - ![]() ------------------------------------------------------------------------------[7.10]
------------------------------------------------------------------------------[7.10]
采用标准方法来最小化此类问题,为了最小化错语,我们必须针对 ![]() 微分这个二次等式[7.9],并将微分结果置为0,并解
微分这个二次等式[7.9],并将微分结果置为0,并解 ![]() 这个方程,产生
这个方程,产生
![]()
∴ ![]() ------------------------------------------------------------------------------------------------------[7.11]
------------------------------------------------------------------------------------------------------[7.11]
总之,这个结果表明,如果我们用函数 g ( x ) = 常数来逼近 f ( x ),给出最佳拟合的常数就是 f ( x ) 的第一个Fourier系数。也就是说,截断Fourier级数也是函数f( x )的“最小二乘估计(least squares estimate)”。
在接受上述结论为普遍正确之前,让我们考虑用 3 项Fourier级数
![]() ------------------------------------------------------------------[7.12]
------------------------------------------------------------------[7.12]
来逼近 f ( x )。
再次,我们使用考察均方误差
ε = f ( x )中的功率 - ![]() 中的功率—----------------------------------------------------------------------------------------------------------------------------------------[7.13]
中的功率—----------------------------------------------------------------------------------------------------------------------------------------[7.13]
中间项在给定信号与模型的三个分量中的每一个分量之间生成三个内积。但是这些内积被认为是Fourier系数的定义。因此错误减少到
ε = f ( x ) 中的功率
![]() --------------------------------------------[7.14]
--------------------------------------------[7.14]
现在,我们首先针对 ![]() 最小化这个错误(译注:对
最小化这个错误(译注:对 ![]() 偏微分 )
偏微分 )
![]()
![]() --------------------------------------------------------------------------------------------------------[7.15]
--------------------------------------------------------------------------------------------------------[7.15]
然后针对 ![]() 最小化这个错误
最小化这个错误
![]()
∴ ![]() -----------------------------------------------------------------------------------------------------[7.16]
-----------------------------------------------------------------------------------------------------[7.16]
然后针对 ![]() 最小化这个错误
最小化这个错误
![]()
∴ ![]() -----------------------------------------------------------------------------------------------------[7.17]
-----------------------------------------------------------------------------------------------------[7.17]
我们再次发现截断Fourier级数也是最小化均方误差的模型。 鉴于这些具体示例,我们无需进一步证明即可断言函数的截断Fourier级数始终是该函数的最小二乘Fourier模型。 这同样适用于部分Fourier级数(即缺少某些项的级数),因为证明基本上是逐项进行的。
请注意,包含基波谐波不会改变第一个示例中确定的最佳常数值。这个结果是由于Fourier级数中基函数的正交性。因此,一般而言,为 k 次谐波计算的最佳Fourier系数与任何其他系数的计算无关。其他不相互正交的拟合(即基)函数的选择,例如多项式或Taylor级数,不具有这个很好的属性。因此,当使用多项式或Taylor级数对数据建模时,获得的系数取决于级数中包含的项数。Fourier级数模型不会出现这种困难,因为基函数是正交的。
我们观察到截断Fourier级数也是最小二乘Fourier模型,这表明了一种处理采样数据不等距分布的两种常见情况的方法。首先,经验记录中可能缺少数据样本,其次,样本可能是在不规则的时间间隔内获得的。在这两种情况下,数据的基函数(三角或复指数)的最小二乘法拟合可用于恢复感兴趣的Fourier系数。 最小二乘算法不像 DFT 那样稳健,并且一次运行一个基函数,但在这种情况下仍然是一种常用的方法。
内容来源:
<< Fourier Analysis for Beginners>> Larry N. Thibos