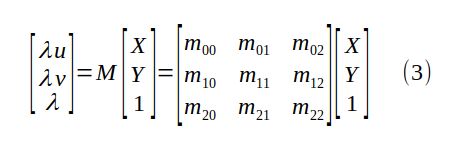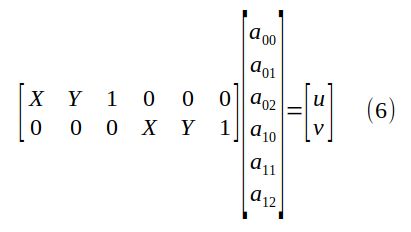数字图像处理的透视变换 vs 仿射变换

你是否注意到，当你拍摄平面矩形物体的图像时，角落的角度很少是90°？

透视投影扭曲的矩形

这种现象是透视投影的特征，其中三维场景中的点（例如，矩形的角）通过针孔¹投影到一个平面（摄像机图像传感器）。靠近摄像机的线段比离摄像机远的相同长度的线段要长。直角可能变成锐角或钝角，并且平行线可能会朝着消失点汇聚。

在对平面物体进行自动检查的情境中，透视失真可能是一个问题。由于我们希望检查对象的特征是否具有正确的形状和大小，我们希望“逆转”透视失真。如果我们能做到这一点，我们就能获得一幅图像，使物体看起来好像摄像机轴垂直于物体表面。

展示了逆转透视失真的效果。在这种情况下，书角被映射到一个带有红色圆圈的正方形状的任意点。右侧的图像更适合自动检查，因为可以轻松地定位并与模板进行比较。

我们想将受透视失真影响的图像扭曲成在兴趣平面上进行恢复的图像：角度失真最小，三维平行线看起来平行。

OpenCV提供了两个功能，可以做到这一点：warpAffine()和warpPerspective()。它们具有相同的签名，但warpAffine()需要一个2x3的变换矩阵，而warpPerspective()需要一个3x3的变换矩阵。这些矩阵分别由函数getAffineTransform()和getPerspectiveTransform()计算。前者期望三对匹配的坐标，而后者期望四对匹配的坐标。直观地说，获得三对比获得四对更容易，因此问题是：在什么情况下我们可以通过三对坐标摆脱使用透视变换而使用仿射变换？

为了回答这个问题，让我们考虑图3中的两幅图像。

左侧：棋盘图像，摄像机距离约1米    右侧：棋盘图像，摄像机距离约7米

尽管棋盘在两次拍摄之间没有移动，但图案看起来不同。在右侧图像中，摄像机距离物体约7米，线的平行性比左侧图像中更好地保持。如果我们计算仿射和透视变换，然后相应地扭曲这些图像，我们得到图4和图5中显示的图像。

图3中图像的仿射变换。棋盘上的点A、B和C被映射到相应的用红色圆圈标记的任意点

图3中图像的透视变换。棋盘上的点A、B、C和D被映射到相应的用红色圆圈标记的任意点

图4显示了仿射变换的效果，使用了点A、B和C。右侧图像，摄于约7米处，得到了合理的补偿，尽管不是完美的（见图6）。左侧图像仍然严重失真，因为点D（甚至在图像中看不到）没有投影到其对应的红色圆圈附近。

图4的细节。点D（蓝色圆盘）被投影到红色圆圈中心附近，但不是完全在中心上

图5显示了透视变换的效果。由于用于计算变换矩阵的四个共面点A、B、C和D，透视失真在两种情况下都得到了很好的补偿，图像看起来相同。我们应该使用的标准是保持线的平行性。仿射变换保持线的平行性。如果待检测的物体在三维世界中具有平行线，而图像中相应的线是平行的（例如图3的右侧情况），那么仿射变换就足够了。相反，如果三维世界中的平行线在图像中发散（例如图3的左侧情况），那么仿射变换就不够了：我们需要透视变换。

透视变换的推导

将平面场景与像素坐标相联系的透视变换来自通过针孔的三维到二维投影的一般情况：

其中f是焦距，(lx, ly)是像素的物理尺寸，(cx, cy)是相机的光学中心，以像素为单位。方程（1）明确显示了针孔相机模型如何将三维点（X，Y，Z）投影到图像坐标（u，v），最终缩放因子λ。从右到左阅读，它会说明：

将世界坐标中的点转换为相机坐标中的坐标，通过旋转和平移，然后将这些坐标投影到传感器平面。

投影矩阵P的形状为3x4。与透视变换的联系来自这样一个假设，即场景（点（X，Y，Z）所在的地方）是一个平面。因此，Z = αX + βY + γ：

将方程（2）中的P的条目与方程（2）中的α，β和γ混合，我们得到一个新的3x3未知矩阵M，透视变换矩阵：

要解出M的条目，我们首先必须在方程（3）中代入，这给了我们关于九个未知数的两个齐次线性方程：

我们可以通过四个对象平面坐标（X，Y）和它们的像素值（u，v）之间的对应关系解出透视变换矩阵M的九个条目（缩放因子），其中四个对应关系（因此八个线性方程）足以。

我们有九个未知数。由于每个对应关系为我们提供了九个未知数中的两个线性方程，为什么四个对应关系（因此八个线性方程）就足够了呢？

因为我们正在处理齐次线性方程，即方程（4）的右侧是零向量。如果我们添加第9个独立线性方程，我们将被困在平凡解

中。通过解四对方程（4）中的线性方程，我们获得的解可以乘以任意非零因子进行缩放。我们通常使用这种自由度设置为：

仿射变换

正如我们前面所述，仿射变换保持线的平行性。这意味着平行四边形将始终映射到另一个平行四边形。当我们使用两个平行四边形的四个对应关系（例如图5的右侧情况）计算透视变换矩阵时，我们观察到条目m_20和m_21非常接近零。您可以通过此脚本在一般四边形和平行四边形之间比较透视变换矩阵，以经验性地检查此观察结果。

映射两个平行四边形的透视变换矩阵的第三行近似为[0 0 1]

如果您对经验观察不满意，这里有一个更有说服力的论点：

将平行四边形映射到另一个平行四边形可以分解为平移、旋转、剪切、轴缩放、剪切、旋转和平移（加上可选的反射）。每个这些变换都可以用其第三行为[0 0 1]的矩阵表示，因此它们的乘

然后可以针对仿射变换的特殊情况的方程（3）写成：

其中我们使用了透视变换矩阵的自由度，任意设置a_{22}=1，通过这样做，我们摆脱了（让人讨厌的）λ乘法器。我们可以重新排列术语，以将仿射变换的条目平铺在一个未知矢量中：

通过（6），每个对应关系为我们提供了6个未知数中的两个线性方程。这就是为什么三个对应关系足以定义仿射变换矩阵的原因。

结论

我们解决了从一组对应关系中映射平面场景的坐标到像素坐标的问题。本文的中心问题是选择哪种类型的变换，透视或仿射。变换没有将对象特征映射到它们的理论位置，除了三个对应点之外。在对透视变换矩阵的起源进行深入挖掘之后，仿射变换矩阵的特殊情况必须注意保持平行性，以便决定变换的类型。

·  END  ·

HAPPY LIFE

本文仅供学习交流使用，如有侵权请联系作者删除