数据结构和算法之十：堆树

数据结构树论之堆树

堆树，作为二叉树中的一个重要成员，常用于优先队列、TOPK等问题中。

在上一文中，我们使用优先队列非常方便的构建出了赫夫曼树，那么你知道优先队列是怎么实现的呢？

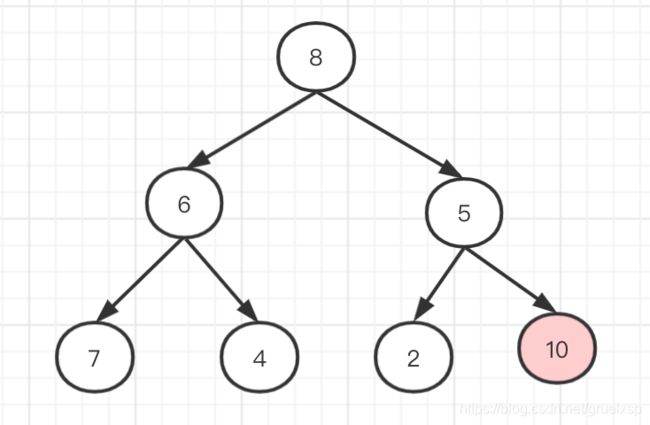
堆树长啥样子，我们先画个图认识一下：（这是大顶堆）

首先，堆树是一颗完全二叉树（完全二叉树的定义你应该还知道吧），同时满足每个父亲节点的值都大于其孩子节点。（每个父亲节点的值都大于其孩子节点的话，就叫小顶堆，为了简化，本文都用大顶堆来举例）

既然堆树是一个完全二叉树，那么我们就可以使用数组来存储，左孩子的下标是父亲节点的2倍，右孩子是2倍+1（根节点的下标从1算起）。

对于一课已经存在的堆树，如何插入一个新的节点？步骤如下

1. 新节点插入到最末尾
2. 新节点从下往上堆化

插入到最末尾容易理解，从下往上堆化是个什么逻辑？这个画个图来理解就非常容易了

比如，上图堆树中新插入6，第一步，将6插入到末尾；然后新节点6和其父亲节点比较，如果大于父亲节点，则和父亲节点交换；然后继续和上一层的父亲节点比较，直到不再交换或者比较到根为止。这个不断和父亲比较和交换的动作，就叫向上堆化。

理解了这个插入的过程，删除元素的核心流程一样，删除分两种情况：

1. 如果删除的是最后一个节点，那么直接删除
2. 删除非最后一个节点时，首先将删除节点和最后一个节点交换，然后执行一次向下堆化；删除最后一个节点即可。

同样，删除画个图理解一下

要删除节点10，首先，将节点10和最后一个节点6交换：

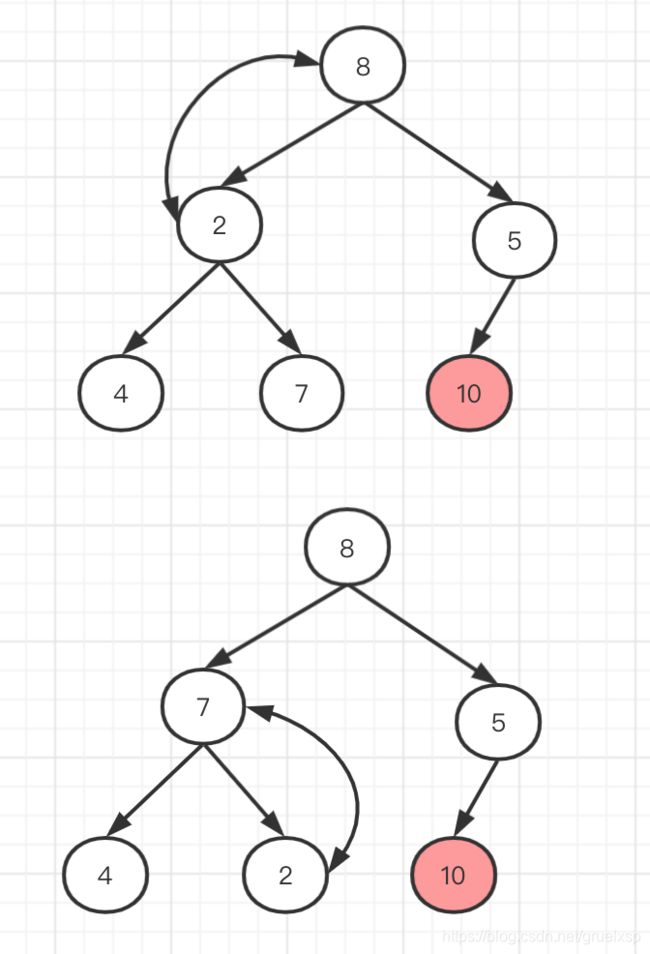
然后对6从上到下进行一次堆化，即和两个孩子比较，如果最大的那个孩子比自己还大，则和最大的孩子交换，示例中的就是6和8交换：

继续往下比较和交换，直到不发生交换，或者交换到叶子节点为止

最后，将节点10删除即可。

通过上面的分析，插入和删除的核心就是堆化，比较和交换的次数最多为logn，因此插入和删除的时间复杂度为logn。

明白了插入和删除，那么构建呢，如果从0开始一个元素一个元素的插入构建，相信大家已经会了；但是如果给你一个数组（也就是一个完全二叉树），如何就在本数组完成堆化呢？

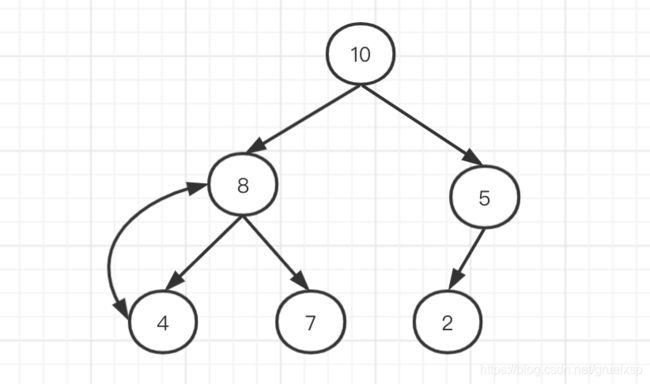
这个过程可以从后往前进行向下堆化即可，从倒数第一个非叶子节点开始即可，因为叶子节点的向下堆化（和孩子比较）是没有任何效果的。同样，图示一波

倒数第一个非叶子节点是5， 它向下堆化后，保持原位。第二次，往前一个位置，对7进行向下堆化，它会和10进行交换；再往前对4进行向下堆化，它会和10交换位置。

因为发生了交换，同时还没有到叶子节点，因此继续往下堆化，与8发生交换。

到此就完成了数组的堆化过程，是不是很巧妙。

可以看出，堆树上的核心操作都和堆化离不开，一定要理解这个堆化的过程。

现在我们可以使用堆树来实现自己的优先队列了，添加元素对应插入，弹出元素就是删除根节点。

在排序算法的两篇文章中，还有一种排序算法没说，那就是堆排序，下面我们来看看堆排序是个什么逻辑。

你应该想到，核心依然是堆化，那么整个流程是怎样的呢？

1. 将根和最后一个节点交换，也就是最大的元素跑到最后去了
2. 然后从根开始往下进行一次堆化（注意堆化的过程排除已经排好序的），完成之后根就变为第二大的元素了
3. 重复1、2步骤，直到剩下最后一个元素为止。

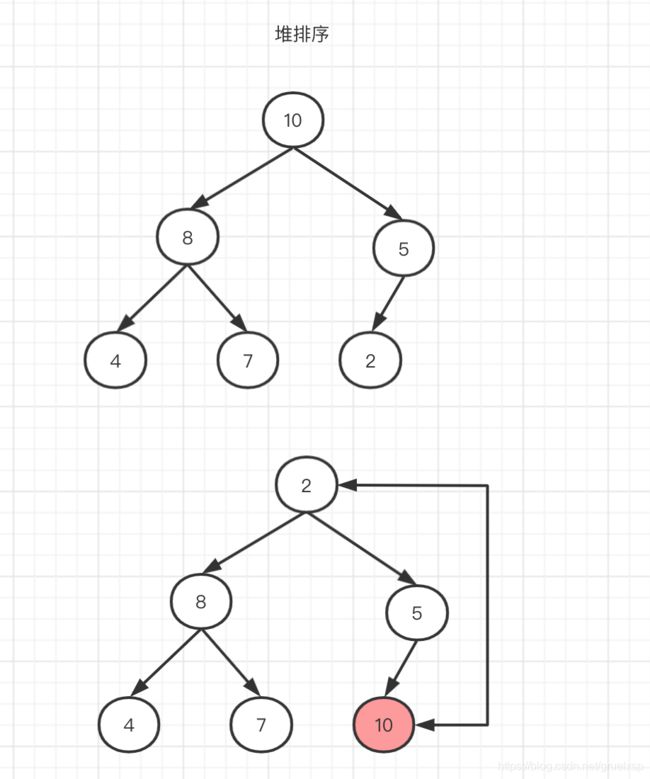
同样，我们画图来理解：

第一步，最大的元素就放到最后了。

第二步，堆化之后第二大的元素就到根上了

重复这个过程，唯一注意的是在堆化时，要排除已经交换到最后去的，已经排好序的元素。

堆树也就这么回事，画画图也就没那么难理解了，最后看下堆树的代码，其中没有实现删除的操作，你能把删除的代码补上吗？

/**
 * 大顶堆树
 *
 *  性质：1。是一颗完全二叉树； 2. 根节点的值大于子节点的值。
 *
 *  因为是一颗完全二叉树，因此可以使用数组存储，数组下标为i的节点，(根节点下标为1)其左孩子下标为2*，右孩子下标为2i+1
 *
 *  堆化过程
 *  情况1， 如果数据是动态的，一个一个插入，可通过两种方式插入处理。
 *  方式1， 从下往上堆化，即新插入的节点，放到最后，然后与其父节点比较，如果大于父亲节点，则交换；沿着往根的路径比较交换下去，直到遇到不交换或者根节点为止。
 *  方式2， 从上往下堆化 
 *
 *  情况2， 如果数据是给定的一个数组，则可直接在原数组上进行堆化。
 *  思路:
 *  从倒数的第一个非叶子开始往前遍历， 往下堆化，直到不能交换或者到叶子节点为止。
 *  画图理解
 *
 *
 *  堆排序
 *  思路
 *  交换根元素（最大值）和最后一个元素，然后从根往下进行一次堆化，注意需要排除当前最后一个元素。重复遍历下去，直到最后一个元素为止。
 *  此时二叉树的中序遍历，也就是数据的下标顺序就是从小到大排序的。
 *  画图理解
 *
 */
public class MaxHeapTree {

    int[] data; //堆数据，完全二叉树，用数组表示， 注意data[0]无意义，根节点从下标1开始。
    int lastIndex; //最后一个节点的索引位置。

    public MaxHeapTree(int[] data) {
        this.data = new int[data.length*2+1]; //为了演示插入，初始化大一点的空间，免得写扩容代码
        this.data[0] = -1; //data[0]占位的，没用
        System.arraycopy(data, 0, this.data, 1, data.length);
        this.lastIndex = data.length;
        maxHeap();
    }

    /**
     * 对数组堆化
     */
    private void maxHeap() {
        //倒数第一个非叶子节点的位置
        int start = lastIndex / 2;
        for (int i = start; i >= 1; i--) {  //从倒数第一个非叶子节点的位置，往前遍历到根
            boolean needStop ;
            int curSubRoot = i;
            do {
                needStop = false;
                //当前非叶子节点为根，与其最大的孩子交换
                int maxChildIndex = 2 * curSubRoot;  //最大的孩子索引位置，初始化为左孩子

                if (2 * curSubRoot + 1 <= lastIndex) { //存在右孩子
                    if (data[maxChildIndex] < data[2 * curSubRoot + 1]) {  //右孩子最大。
                        maxChildIndex = 2 * curSubRoot + 1;
                    }
                }

                if (data[curSubRoot] < data[maxChildIndex]) { //当前比最大的孩子小，需要交换位置
                    int temp = data[curSubRoot];
                    data[curSubRoot] = data[maxChildIndex];
                    data[maxChildIndex] = temp;

                    curSubRoot = maxChildIndex; //当前子树根指向交换之后的位置。
                }else{
                    needStop = true; //如果没有发生交换了，就可以停止了。
                }

                if(2 * curSubRoot > lastIndex){ //没有孩子节点了，也就是已经是叶子节点了，也停止
                    needStop = true;
                }

            }while (!needStop);

        }
    }

    /**
     * 动态插入
     * @param value
     */
    public void insert(int value){

        if(lastIndex < data.length){  //容量还够，插入到最后
            data[++lastIndex] = value;
        }
        //从下到上堆化
        int curChildIndex = lastIndex;
        int parentIndex = curChildIndex / 2;
        while(parentIndex >= 1){        //遍历到根，除非中途跳出循环。
            if(data[parentIndex] < data[curChildIndex]){  //当前父亲节点小于孩子节点，交换
                int temp = data[parentIndex];
                data[parentIndex] = data[curChildIndex];
                data[curChildIndex] = temp;

                curChildIndex = parentIndex;
                parentIndex = curChildIndex / 2;
            }else{
                break; //没有发生交换时，退出循环
            }
        }

    }

    /**
     * 堆排序
     */
    public void sort(){

        //堆顶和最后一个可以交换的节点交换
        int curCanSwapIndex = lastIndex;

        while(curCanSwapIndex >= 2) {
            int temp = data[1];
            data[1] = data[curCanSwapIndex];
            data[curCanSwapIndex] = temp;

            //从根开始，往下堆化
            boolean needStop;
            int curSubRoot = 1;
            do {
                needStop = false;
                //当前根，与其最大的孩子交换，需要注意的是孩子节点不是堆顶交换下去的。
                int maxChildIndex = 2 * curSubRoot;  //最大的孩子索引位置，初始化为左孩子
                if (maxChildIndex >= curCanSwapIndex) { //左孩子已经是堆顶交换下去的了，跳出堆化
                    break;
                }

                if (2 * curSubRoot + 1 <= curCanSwapIndex - 1) { //确保右孩子也不是堆顶交换下来的
                    if (data[maxChildIndex] < data[2 * curSubRoot + 1]) {  //右孩子最大。
                        maxChildIndex = 2 * curSubRoot + 1;
                    }
                }

                if (data[curSubRoot] < data[maxChildIndex]) { //当前比最大的孩子小，需要交换位置
                    int temp2 = data[curSubRoot];
                    data[curSubRoot] = data[maxChildIndex];
                    data[maxChildIndex] = temp2;

                    curSubRoot = maxChildIndex; //当前子树根指向交换之后的位置。
                } else {
                    needStop = true; //如果没有发生交换了，就可以停止了。
                }

            } while (!needStop);

            curCanSwapIndex--; //往前走
        }

    }


    public static void main(String[] args) {
        MaxHeapTree heapTree = new MaxHeapTree(new int[]{3, 8, 2, 4, 9, 7, 10, 23});
        System.out.println(Arrays.toString(heapTree.data));

        heapTree.insert(20);
        System.out.println(Arrays.toString(heapTree.data));

        heapTree.insert(25);
        System.out.println(Arrays.toString(heapTree.data));

        heapTree.sort();
        System.out.println(Arrays.toString(heapTree.data));
    }


}

最后通过堆排序可视化复习下核心的堆化过程：
https://www.cs.usfca.edu/~galles/visualization/HeapSort.html