leetcode:373. 查找和最小的 K 对数字
题目来源
- leetcode:373. 查找和最小的 K 对数字
题目描述
class Solution {
public:
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
}
};
题目解析
分析数据
- 数据量非常大,如果两两比较,肯定会超时,所以需要优化
![]()
-
数据范围很大

-
如果在nums1中选取k个元素,在nums2中选取k个元素,组合最大复杂度是O(10^6),可以通过
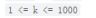
归并
对于例子nums1 = [1,7,11], nums2 = [2,4,6],我们可以构造出三条递增的有序链表,如下图所示:

我们再来分析一下时间复杂度,假设 n = nums1.length, m = num2.length
按照上图的方法构造有序链表的话,每次需要从 n 个元素中找出最小的元素,需要找 k 次,所以时间复杂度为 O(klogn)
所以为了更优的时间复杂度,尽量让 nums1 长度更短;如果 nums1 长度更长,我们就交换两个数组的位置
class Solution {
bool flag = true; // 标志是否交换了位置 true : 未交换;false : 交换了
public:
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
int n = nums1.size(), m = nums2.size();
if (n > m && !(flag = false))
return kSmallestPairs(nums2, nums1, k);
// 注意:队列中存储的只是下标
// 按照「两数和」递增排列 小顶堆
auto cmp = [&](const auto& a, const auto& b){
return nums1[a.first] + nums2[a.second] > nums1[b.first] + nums2[b.second];
};
priority_queue< pair<int,int>, vector<pair<int,int>>, decltype(cmp) > q(cmp);
// 加入头节点
// 这里有一个技巧:如果 k < n,那么一开始只需要往队列中添加前 k 个元素即可
// 后面的 n - k 个元素肯定比前面 k 个元素大,所以加入没有意义
for (int i = 0; i < std::min(n, k); ++i) {
q.push({i, 0});
}
vector<vector<int>> ans;
while (ans.size() < k && !q.empty()){
auto curr = q.top(); q.pop(); // 弹出队顶元素,即最小元素
int a = curr.first, b = curr.second;
flag ? ans.push_back( {nums1[a], nums2[b]}) : ans.push_back( {nums2[b], nums1[a]});
// 如果 b + 1 < m 表示该条链条后面还有元素,可以继续加入队列中
if(b + 1 < m){
q.push({a, b + 1});
}
}
return ans;
}
};
思路二
对于类似找集合中最小的k个元素问题,一个基本思路是:
- 将候选元素加入到小顶堆中,然后不断取出堆顶元素,并将新产生的候选元素入堆
需要注意的是:
- 候选元素必须包含当前的最小元素
- 候选元素越少越好,因为堆调整的时间会缩短
本题的数对可以用一个矩阵表示,如下图所示。上面多路归并实际上是将每一行的首元素都作为候选元素,显然这满足条件一,但并不是最优的选取方法,还有更少的候选元素的选取方式。
对于例子nums1 = [1,7,11], nums2 = [2,4,6],有如下:

首先,可以得出的一个结论是:所有的左下角中一定包含当前最小元素
- 为什么说“所有的左下角点”,是因为元素被选择后,矩阵中剩余的元素会形成很多左下角点。用反证法可以非常容易的说明上述结论:对于矩阵中的任意一个指标(i,j),如果它不是作为左下角点,则一定存在还未被选择的(i-1,j)或者(i,j-1),而这两个位置的数必然比它小,因为它不可能是当前的最小元素
- 综上所述,可以将所有的左下角点作为候选元素,这就大大减少候选元素的数量。动画
class Solution {
public:
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
int n = nums1.size(), m = nums2.size();
// 小顶堆
auto greater = [&](pair<int, int>& x, pair<int, int>& y){
return nums1[x.first] + nums2[x.second] > nums1[y.first] + nums2[y.second];
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(greater)> que(greater);
vector<vector<int>> ans;
vector<int> coltop(m + 1, 0); // 记录每一列对应下一个候选元素纵坐标 i 0~n-1
coltop[0] = n;
que.push({0, 0}); // 第一个左下角点入堆
for(int cnt=0; cnt < k && cnt < (long)n*m; ++cnt){
auto [i, j] = que.top(); que.pop();
ans.push_back({nums1[i], nums2[j]});
// 更新第 j 列已选高度
++coltop[j + 1];
// 若第 j 列比 j-1 列矮,j 列顶端是一个新角点
if(coltop[j + 1] < coltop[j])
que.push({coltop[j + 1], j});
// 若第 j+1 列刚好比 j 列矮一格, 第 j+1 列顶端是一个新角点
if(j <= m-2 && coltop[j+2] == coltop[j+1] - 1)
que.push({coltop[j + 2], j + 1});
}
return ans;
}
};
思路(暴力剪枝)
- 从0循环到数组的个数和k之间的较小值,然后将其都保存在 res 里
- 给 res 排序,用自定义的比较器,就是和的比较,然后把比k多出的数字对删掉即可
class Solution {
public:
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
int n = nums1.size(), m = nums2.size();
vector<vector<int>> ans;
for (int i = 0; i < min(n, k); ++i) {
for (int j = 0; j < min(m, k); ++j) {
ans.push_back({nums1[i], nums2[j]});
}
}
// 找和最小的K对数字 ^,
sort(ans.begin(), ans.end(), [](pair<int, int> &a, pair<int, int> &b){return a.first + a.second < b.first + b.second;});
if(ans.size() > k){
ans.erase(ans.begin() + k, ans.end());
}
return ans;
}
};
- 我们可以用mutilmap来做,思路是将数组对之和作为key存入mutimap中
- 利用mutilmap的自动排序机制可以省去sort的步骤
- 最后将钱k个元素存入res中即可
class Solution {
public:
vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
int n = nums1.size(), m = nums2.size();
std::multimap<int, std::pair<int, int>> map;
for (int i = 0; i < min(n, k); ++i) {
for (int j = 0; j < min(m, k); ++j) {
map.insert({nums1[i] + nums2[j], {nums1[i], nums2[j]}});
}
}
// 找和最小的K对数字 ^,
vector<vector<int>> ans;
for (auto & it : map){
ans.push_back({it.second.first, it.second.second});
if (--k <= 0) return ans;
}
return ans;
}
};
- 下面这种方式用了 priority_queue,也需要我们自定义比较器,整体思路和上面的没有什么区别:
class Solution {
public:
vector<pair<int, int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
vector<pair<int, int>> res;
priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> q;
for (int i = 0; i < min((int)nums1.size(), k); ++i) {
for (int j = 0; j < min((int)nums2.size(), k); ++j) {
if (q.size() < k) {
q.push({nums1[i], nums2[j]});
} else if (nums1[i] + nums2[j] < q.top().first + q.top().second) {
q.push({nums1[i], nums2[j]}); q.pop();
}
}
}
while (!q.empty()) {
res.push_back(q.top()); q.pop();
}
return res;
}
struct cmp {
bool operator() (pair<int, int> &a, pair<int, int> &b) {
return a.first + a.second < b.first + b.second;
}
};
};
类似题目
多路归并
- leetcode:21. 合并两个有序链表
- leetcode:23. 合并K个升序链表
- 将n个有序链表的头结点加入小根堆的优先队列中,由于n个链表都是递增的顺序,所以第一个最小的元素一定在这n个头结点中产生
- 选择最小元素后,将该最小元素所在的链表后移一位,并将后一位元素加入队列中,依次类推…
- leetcode:264. 返回第n个丑数 II
- leetcode:313. 返回第n个丑数 III
- leetcode:373. 查找和最小的 K 对数字 Find K Pairs with Smallest Sums
- leetcode:378. 有序矩阵中第 K 小的元素 Kth Smallest Element in a Sorted Matrix
- leetcode:786. 第 K 个最小的素数分数 K-th Smallest Prime Fraction
- leetcode:1508. 子数组和排序后的区间和
- leetcode:719. 找出第 K 小的数对距离
- leetcode:1439. 有序矩阵中的第 k 个最小数组和
