第五章总结
1.1 数组的概述
数组是具有相同数据类型的一组数据的集合。
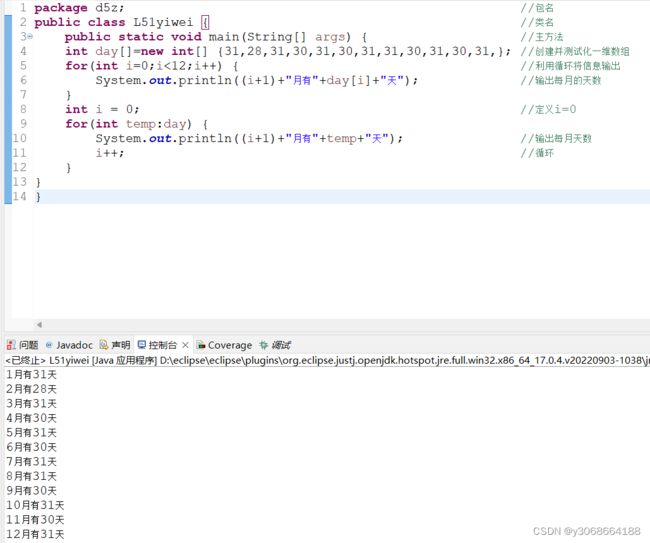
1.2 一维数组
一维数组实质上是一组相同类型数据的线性集合,例如学校中学生们排列的一字长队就是一个数组,每一位学生都是数组中的一个元素。
1.2.1 创建一维数组
数组元素类型决定了数组的数据类型。它可以是Java中任意的数据类型,包括基本数据类型和其他引用类型。数组名字为一个合法的标识符,符号"[]"指明该变量是一个数组类型变量。单个"[]表示要创建的数组是一个一维数组。
声明一维数组有两种方式:
数组元素类型 数组名字[];
数组元素类型[] 数组名字;
声明一维数组,语法如下:
int arr[]; //声明int型数组,数组中的每个元素都是int型数值
数组名字=new数组元素的类型[数组元素个数];
代码中ar为数组名称,方括号“[]”中的值为数组的下标,也叫索引。数组通过下标来区分不同的元素,也就是说,数组中的元素都可以通过下标来访问。这就相当于刚才比喻一个酒店,我们想要找到某个房间里的人,只需要知道这个人所在房间号。这个房间号就相当于数组的下标,
数组的下标是从0开始的。
为数组分配内存,代码如下
arr=new[5]
以上代码表示要创建一个含有5个元素的整型数组,并将创建的数组对象赋给引用变量arr。
一维数组分配图
arr——>arr[0], arr[1], arr[2], arr[3], arr[4].
1.2.2 初始化一维数组
数组可以与基本数据类型一样进行初始化操作,也就是赋初值。数组的初始化可分别初始化数组中的每个元素。数组的初始化有以下种方式:
int arr2[]={34,23,12,6}; //第二种方式
int arr[]=new int[] {1,2,3,5,25}; //第一种方式
数组的初始化就是包括在大括号之内用逗号分开的表达式列表。用逗号“,”分隔数组中的各个元素,系统自动为数组分配一定的空间。第一种初始化方式,将创建5个元素的数组,依次为1,2,3,5,25;第二种初始化方式,创建4个元素的数组,依次为34,23,12,6
1.2.3使用一维数组
1.3 二维数组
二维数组常用于表示表,表中的信息以行和列的形式表示,第一个下标代表元素所在的行,第二个下标代表元素所在的列。
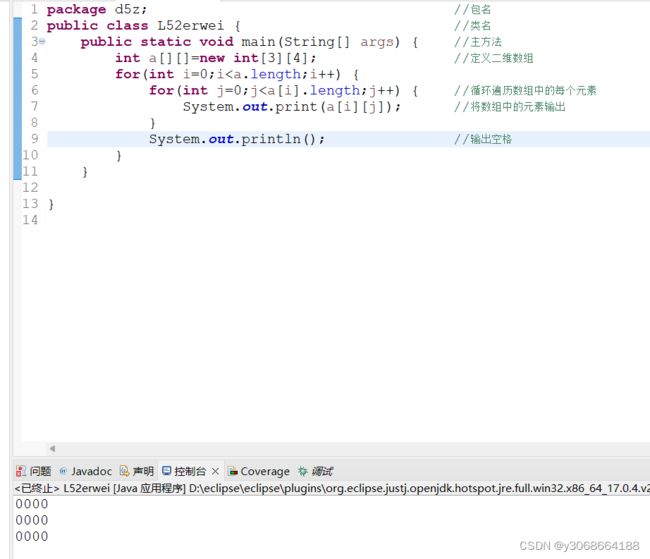
1.3.1 创建二维数组
二维数组可以看作是特殊的一维数组,二维数组有两种声明方式:
数组元素类型 数组名字[][];
数组元素类型[][] 数组名字;
声明二维数组。第一种,代码如下:
int a[][];
同一维数组一样,二维数组在声明时也没有分配内存空间,同样要使用关键字new来分配内存,然后才可以访问每个元素。
a=new int[2][4]; //直接分配行列
二维数组分配图
a length=2.
length1 a[0][0] a[0][1] a[0][2] a[0][3]
length2 a[1][0] a[1][1] a[1][2] a[1][3]
声明二维数组。第二种,代码如下:
b=new int[2][]; //先分配行,不分配列
b[0]=new int[2]; //给第一行分配列
b[1]=new int[2]; //给第二行分配列
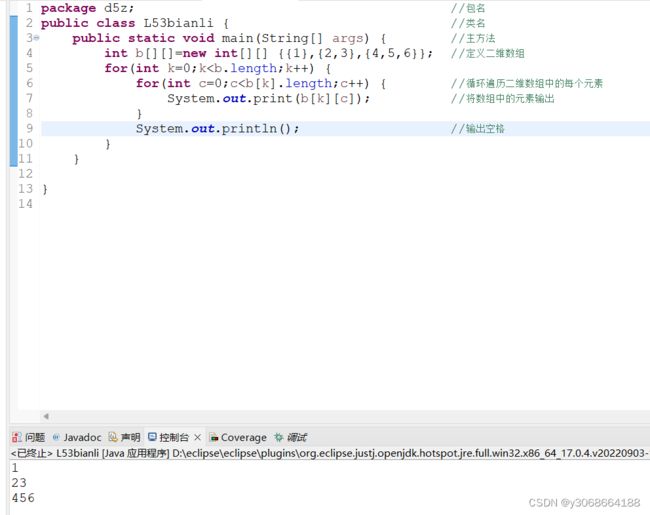
1.3.2 初始化二维数组
二维数组的初始化方式与一维数组类似,同样使用大括号完成。语法如下:
type arryname[][]={value1,value1,....valuen,};
type:数组数据类型.
arrayname:数组名称,一个合法的标识符。
value:二维数组中各元素,都代表一个一维数组。
初始化二维数组 代码如下:
int myar[][]={{12,0},{45,10}};
初始化二维数组后,要明确数组的下标都是从0开始。例如,上面代码中myarr[1][1]的值为10.
1.3.3使用二维数组
二维数组在实际中应用的非常广泛。
1.4数组的基本操作
1.4.1遍历数组
遍历数组就是获取数组中的每个元素。通常遍历数组都是使用for循环来实现。遍历一维数组很简单,也很好理解,下面详细介绍遍历二维数组的方法。
遍历二维数组要使用两层for循环,通过数组的length属性可获得数组长度。
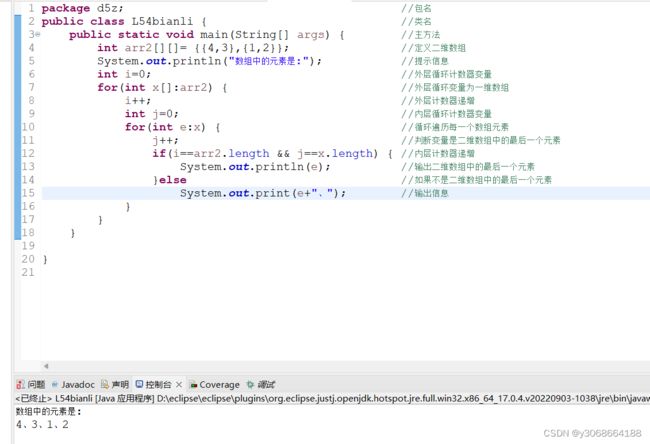
在遍历数组时,使用foreach语句可能会更简单。
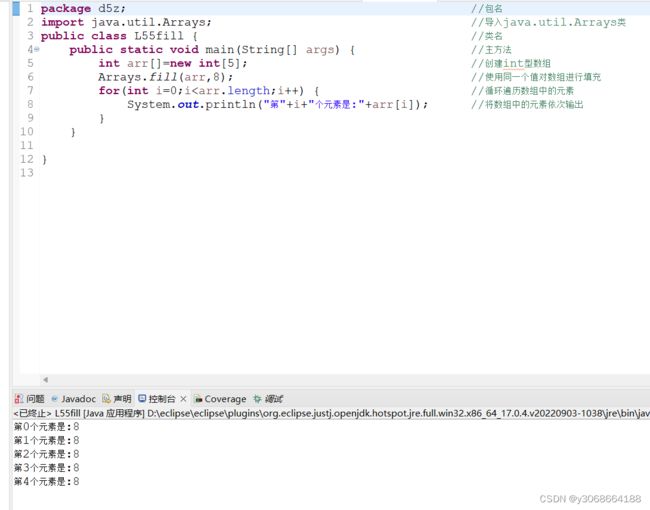
1.4.2填充替换数组元素
数组中的元素定义完成后,可通过arrays类的静态方法fill()来对数组中的元素进行替换。该方法通过各种重载形式可完成对任意类型的数组元素的替换。fill()方法有两种参数类型,下面int类型数组
fill(int[] a,int value)
a:要进行元素替换的数组。
value:要存储数组中的所有元素的值。
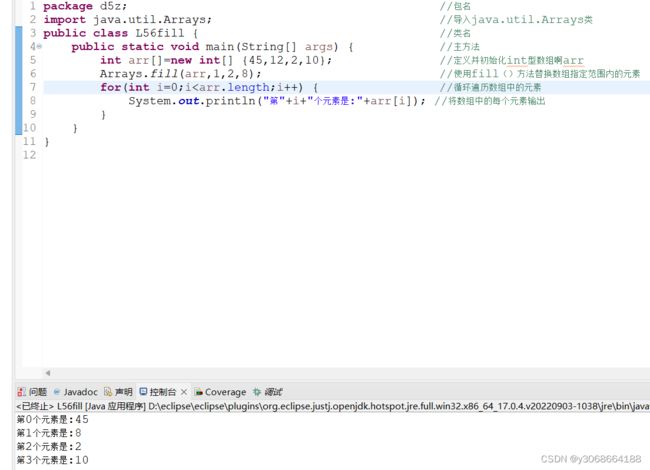
fill(int[] a, int fromlndex,int tolndex,int value)
a:要进行填充的数组
fromlndex:要使用指定值填充的第一个元素的索引(包括)
tolndex:要使用指定值填充的最后一个元素的索引(不包括)
value:要分配给数组指定范围中的每个元素的值
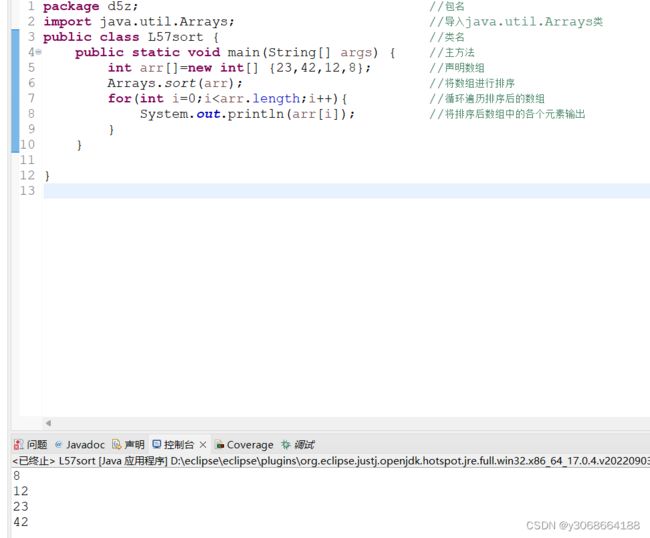
1.4.3对数组进行排序
通过arrays类静态方法sort()可以实现对数组的排序。sort()方法提供了多种重载形式,可对任意类型数组进行升序排序。语法如下:
array.sort(object)
object:是指进行排序的数组名称。
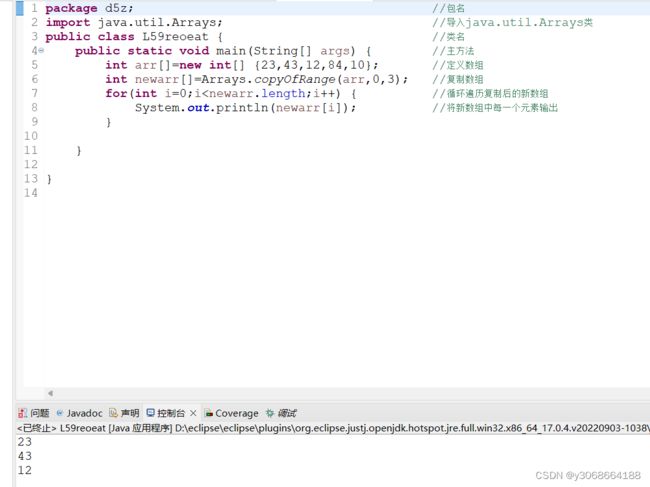
1.4.4复制数组
Arrays类的copy OP()方法与copyOFRange()方法可以实现对数组的复制。copy OP()方法是复制数组至指定长度,copyOFRange()方法则是将指定数组的长度复制道应该新的数组中
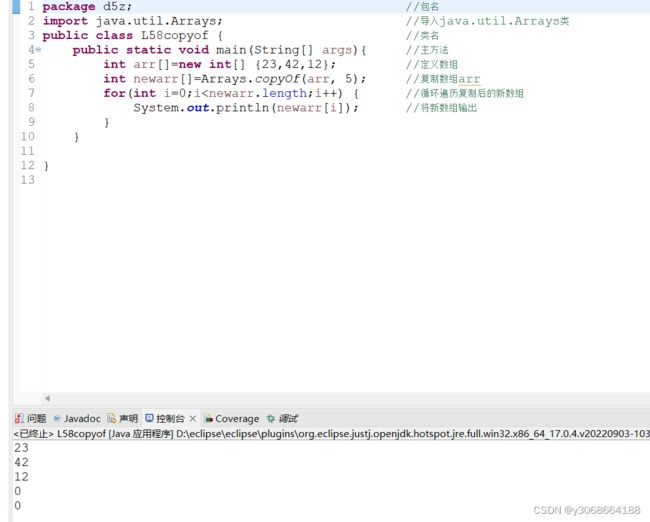
1.copyOF()方法
该方法提供了多种重载形式,用于满足不同类型数组的复制。语法如下:
copyO(arr,int newlength)
arr:要进行复制的数组。
newlength:int型常量,指复制后的新数组的长度。如果新数组的长度大于数组arr的长度,则用0填充(根据复制数组的类型来决定填充的值,整数数组用0填充,char型数组则使用null来填充);如果复制后的数组长度小于数组arr的长度,则会从数组arr的第应该元素开始截取至满足新数组长度为止。
2.copyOFRange()方法
该方法同样提供了多种重载形式。代码如下:
copyO(arr,int fromlndex,int tolndex)
arr:要进行复制的数组对象。
fromlndex:指定开始复制数组的索引位置。fromlndex必须在0至整个数组的长度之间。新数组包括索引是fromlndex的元素。
tolndex:要复制范围的最后索引位置。可大于数组arr的长度。新数组不包括索引是tolndex的元素。
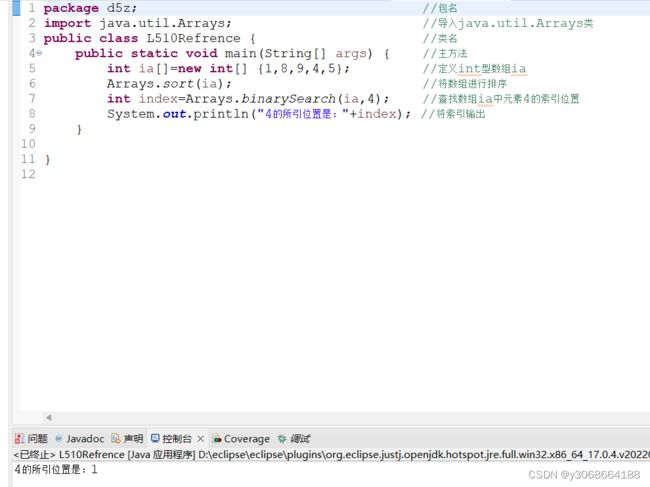
1.4.5查询数组
Arrays类的binarySearch()方法,可使用二分搜索法来搜索指定数组,以获得指定对象。该方法返回要搜索元素的索引值。binarySearch()方法提供了多种重载形式,用于满足各种类型数组的查找需要,binarySearch()方法有两种参数类型。
1.binarySearch(Object[]a,Object key)
binarySearch(Object[]a,Object key)
a:要搜索的数组。
key:要搜索的值
如果key包含在数组中,则返回搜索值的索引;。否则返回-1或“-”()插入点。插入点是搜索键将要插入数组的那一个点,即第一个大于此键的元素索引
2.binarySearch(Object[]a,int fromlndex,int tolndex,Object key)
该方法在指定的范围内搜索某一元素。
binarySearch(Object[]a,int fromlndex,int tolndex,Object key)
a:要进行搜索的数组。
fromlndex:指定范围的开始处索引(包括)。
tolndex:指定范围的结束处索引(不包括)。
key:要搜索的元素。
在使用该方法前,同样要进行数组排序,这样才能获得准确的索引值。如果搜索的元素key在指定范围内,则返回搜索键;否则返回-1或“-”()插入点。如果范围中的所有元素都小于指定键,则插入点位tolndex(注意,这保证了当且仅此键被找到时,返回的值将大于等于0)。
1.5数组排序算法
1.5.1冒泡排序
1.基本思想
冒泡排序的基本思想是对比相邻的元素值,如果满足条件就交换元素值,把较小的元素移动到数组前面,把较大的移动到数组后面(也就是交换了两个元素的位置),这样较小的值就会像冒泡泡一样从底部上升到顶部。
2算法示例
| 63 | 4 | 4 | 1 | 1 | 1 |
| 4 | 24 | 1 | 3 | 3 | 3 |
| 24 | 1 | 3 | 4 | 4 | 4 |
| 1 | 3 | 15 | 15 | 15 | 15 |
| 3 | 15 | 24 | 24 | 24 | 24 |
| 15 | 63 | 63 | 63 | 63 | 63 |
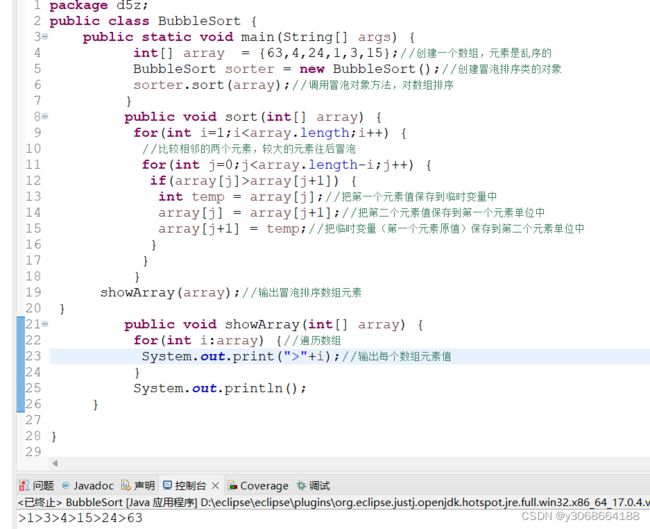
3.算法实现
1.5.2直接选择排序
直接选择排序属于选择排序的一种,它的排序速度要比冒泡排序快一些,也是常用的排序算法,初学者应该掌握。
1.基本思想
直接选择排序的基本思想是将指定排序位置元素与其他数组元素分别做对比,如果满足条件就交换元素值。注意这里与冒泡排序的区别,不是交换相邻的元素,而是把满足条件的元素与指定的排序位置元素交换(如从最后一个元素开始排序),这样排序好的位置逐渐扩大,直至整个数组都已变成已排序好的格式。
这就好比一个小学生,从包含数字1~10的乱序的数字堆中分别选择合适的数字,组成一个1~10的排序,而这个小学生首先从数字堆中选出1,放到第一位,然后选出2(注意这时数字堆中已经没有1了)放在第二位,以此类推,直至其找到9,放到8的后面,最后剩下的10,就不用选择了直接放到最后就可以。
与冒泡排序相比,直接选择排序的交换次数要少很多,所以速度会快一些。
2算法示例
每一趟从待排序的数组元素中选最大(或最小)的元素,顺序地放在已排序的数列最后,直至全部待排序的数据元素排序完
| 【63 | 4 | 24 | 1 | 3 | 15】 |
| 【15 | 2 | 24 | 1 | 3】 | 63 |
| 【15 | 2 | 3 | 1】 | 24 | 63 |
| 【1 | 4 | 3】 | 15 | 24 | 63 |
| 【1 | 3】 | 4 | 15 | 24 | 63 |
| 【1】 | 3 | 4 | 15 | 24 | 63 |
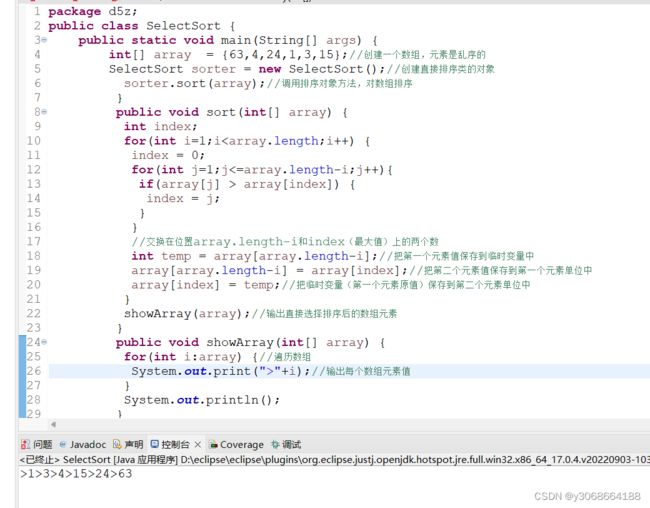
3.算法实现
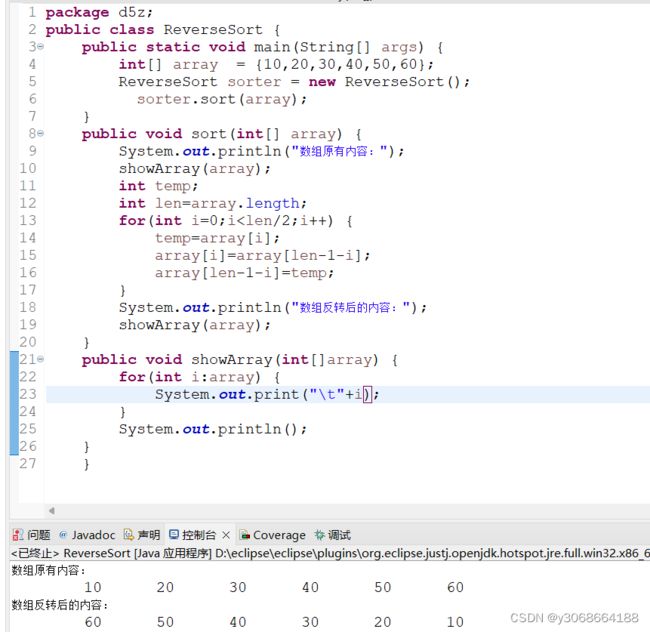
1.5.3反转排序
顾名思义,反转排序就是以相反的顺序把原有的数组内容重新排序。反转算法在程序开发中也经常用到。
1.基本思想
反转排序的基本思想比较简单,也很好理解,其实现思路就是把数组最后一个元素与第一个元素替换,倒数第二个元素与第二个元素替换,以此类推,直到把所有数组元素都反转替换。
2算法示例
反转排序是对数组的两边元素进行替换,所以只需要循环数组长度的一半数次,如数组长为7只要循环三次
| 初始数组资源 | 【10 | 20 | 30 | 40 | 50 | 60】 |
| 第一趟排序后 | 60 | 【20 | 30 | 40 | 50】 | 10 |
| 第二趟排序后 | 60 | 50 | 【30 | 40】 | 20 | 10 |
| 第三趟排序后 | 60 | 50 | 40 | 30 | 20 | 10 |
3.算法实现