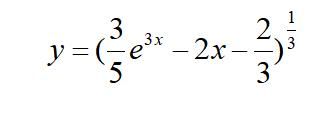微分方程建模与求解
一、问题背景和实验目的
自牛顿发明微积分以来,实际应用问题通过数学建模所得到的方程,绝大多数是微分方程。
由于实际应用的需要,但能够求得解析解的微分方程十分有限,绝大多数微分方程需要利用数值方法来近似求解。
本文章主要研究如何用 Matlab 来计算微分方程(组)的数值解。
二、五种常用方法
1.Euler折线法
基本思想:用差商代替微商
具体步骤 :分割求解区间,差商代替微商,解代数方程
话不多说,直接上例子:
MATLAB程序:
clear
f=sym('y+2*x/y^2');
a=0; b=2;
h=0.4;
n=(b-a)/h+1; % n=(b-a)/h;
x=0; y=1;
szj=[x,y];
for i=1:n-1 % i=1:n
y=y+h*subs(f,{'x','y'},{x,y});
x=x+h;
szj=[szj;x,y];
end
szj
plot(szj(:,1),szj(:,2),'or-')
2.Runge-Kutta (龙格-库塔) 法
在Euler折线法的基础上:为了减小误差,可采用以下方法:
- 让步长 h 取得更小一些;
- 改用具有较高精度的数值方法:Runge-Kutta (龙格-库塔) 方法
Runge-Kutta (龙格-库塔)是一类求解常微分方程的数值方法,有多种不同的迭代格式
MATLAB程序:
clear;
f=sym('y+2*x/y^2');
a=0; b=2; h=0.4;
n=(b-a)/h+1; % n=(b-a)/h;
x=0; y=1;
szj=[x,y];
for i=1:n-1 % i=1:n
l1=subs(f,{'x','y'},{x,y});
l2=subs(f,{'x','y'},{x+h/2,y+l1*h/2});
l3=subs(f,{'x','y'},{x+h/2,y+l2*h/2});
l4=subs(f,{'x','y'},{x+h,y+l3*h});
y=y+h*(l1+2*l2+2*l3+l4)/6;
x=x+h;
szj=[szj;x,y];
end
plot(szj(:,1),szj(:,2), 'dg-')
3.欧拉公式
4.梯形方法
5.改进欧拉公式
三、关于Matlab 解初值的问题
1.背景
对于许多实际问题,人们建立了相应的微分方程,并探讨了一些理论求解方法,并利用解来解释实际现象,对特定问题进行分析、控制等。
但当前,理论成果主要体现在特定类型下的微分方程求解,多数情况下不能得到理论解(解析解)。
对于一些复杂微分方程,即使是一阶的,求解也很困难,有时候得到的是隐式解,有时候无法得到解析解。
当对于某些微分方程不能得到解析解时,人们一般去求微分方程的数值解。
2.常用求解函数
dsolve 的使用:
y=dsolve(‘eq1’,‘eq2’, … ,‘cond1’,‘cond2’, … ,‘v’)
其中 y 为输出, eq1、eq2、…为微分方程,cond1、cond2、…为初值条件,v 为自变量。
几点说明:
-
微分方程中用 D 表示对 自变量 的导数,如:
Dy -> y’ D2y -> y’’ D3y -> y’’’ -
如果省略初值条件,则表示求通解;
如果省略自变量,则默认自变量为 t
dsolve(‘Dy=2x’,‘x’); % dy/dx = 2x
dsolve('Dy=2x’); % dy/dt = 2x
若找不到解析解,则返回其积分形式。
[T,Y] = solver(odefun,tspan,y0)
其中 y0 为初值条件,tspan为求解区间;Matlab在数值求解时自动对求解区间进行分割,T (向量) 中返回的是分割点的值(自变量),Y (向量) 中返回的是解函数在这些分割点上的函数值。
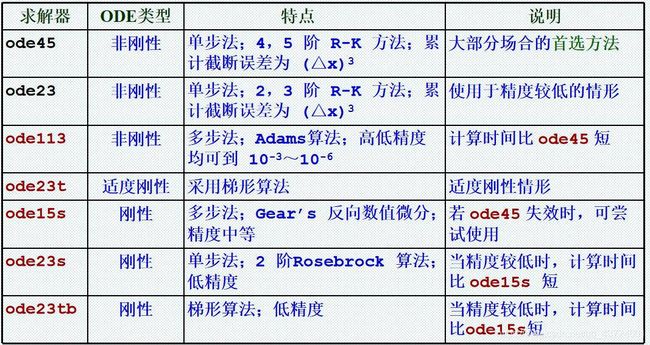
solver 为Matlab的ODE求解器(可以是 ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb)
没有一种算法可以有效地解决所有的 ODE 问题,因此MATLAB 提供了多种ODE求解器,对于不同的ODE,可以调用不同的求解器。
3.求解器的选择
解析解:dsolve
求数值解: ode45、ode23、 ode113、ode23t、ode15s、ode23s、ode23tb