Hinge loss

声明：

1. 参考自维基百科
2. 后面可能会更新

Hinge Loss

  在机器学习中，hinge loss作为一个损失函数(loss function)，通常被用于最大间隔算法(maximum-margin)，而最大间隔算法又是SVM(支持向量机support vector machines)用到的重要算法(注意：SVM的学习算法有两种解释：1. 间隔最大化与拉格朗日对偶；2. Hinge Loss)。

  Hinge loss专用于二分类问题，标签值 y=±1 y = ± 1 ，预测值 ŷ ∈R y ^ ∈ R 。该二分类问题的目标函数的要求如下：
  当 ŷ  y ^ 大于等于+1或者小于等于-1时，都是分类器确定的分类结果，此时的损失函数loss为0；而当预测值 ŷ ∈(−1,1) y ^ ∈ ( − 1 , 1 ) 时，分类器对分类结果不确定，loss不为0。显然，当 ŷ =0 y ^ = 0 时，loss达到最大值。

  如果你想到了一个可以定义这种loss的函数，那说明有成为数学家的潜质。想不到的话就乖乖的往下看：hinge loss出场。
  对于输出 y=±1 y = ± 1 ，当前 ŷ  y ^ 的损失为：

ℓ(y)=max(0,1−y⋅ŷ ) ℓ ( y ) = max ( 0 , 1 − y ⋅ y ^ )

上式是Hinge loss在二分类问题的的变体，可以看做双向Hinge loss。难以理解的话，可以先看单方向的hinge loss。以y=+1，为例。当 y⩾1 y ⩾ 1 时，loss为0，否则loss线性增大。函数图像如下所示：

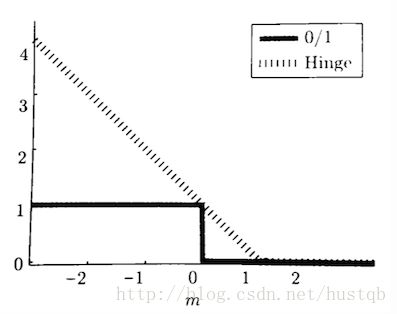
图片来源： 机器学习基础（四十二）—— 常用损失函数的设计（multiclass SVM loss & hinge loss）

Hinge loss在SVM中的应用

  SVM在简单情况下（线性可分情况下）使用的就是一个最大间隔算法。几何意义如下图所示（实心的数据点就是该类别的支持向量），最大化分离超平面到两个类别的支持向量之间的距离 。

图片来源： 知乎-支持向量机(SVM)是什么意思？
  线性可分SVM的预测值 ŷ =w⋅x+b y ^ = w ⋅ x + b ，其中 w w 和b b 都是分类器通过样本学习到的参数。正如前面所说， ŷ ∈R y ^ ∈ R 。如果分离超平面在如上图所示的位置（这是最大分割情况）并且支持向量与分割平面之间的距离=1，每个 y=1 y = 1 的样本其 ŷ ⩾1 y ^ ⩾ 1 ，每个 y=−1 y = − 1 的样本其 ŷ ⩽−1 y ^ ⩽ − 1 ，每个点的Hinge loss为0，整体loss作为平均值，也等于0。 如果分割超平面误分类，则Hinge loss大于0。Hinge loss驱动分割超平面作出调整。 如果分割超平面距离支持向量的距离小于1，则Hinge loss大于0，且就算分离超平面满足最大间隔，Hinge loss仍大于0

拓展

  再强调一下，使用Hinge loss的分类器的 ŷ ∈R y ^ ∈ R 。 |ŷ | | y ^ | 越大，说明样本点离分割超平面越远，即该样本点很容易被分类。但是，我们在选择合适的损失函数进行优化时，没必要关注那些离超平面很远的样本。为此，我们可以通过对距分离超平面的距离选择一个阈值，来过滤这些离超平面很远的样本。这就是Hinge loss的精髓， ℓ(y)=max(0,1−y⋅ŷ ) ℓ ( y ) = max ( 0 , 1 − y ⋅ y ^ ) ，式中的1就是我们选择的阈值，这个可以作为一个超参数。通过一个max(0, )函数，忽略 ŷ  y ^ 值过高的情况。

SVM

  这个思想可以拓展到SVM的多分类问题。SVM的多分类有两种损失函数：

ℓ(y)=max(0,1+maxŷ ≠ywŷ x−wyx) ℓ ( y ) = max ( 0 , 1 + max y ^ ≠ y w y ^ x − w y x )

其中， maxŷ ≠y(wŷ x+b) max y ^ ≠ y ( w y ^ x + b ) 表示对于某一标签值 y y ，分类器错误预测的最大值，wyx+b w y x + b 表示正确的分类器预测值， 1 1 表示分类阈值。注意：即使是分类器，也是先产生预测值，再根据预测值和分类阈值进行分类的。

ℓ(y)=∑t≠ymax(0,1+wŷ x−wyx) ℓ ( y ) = ∑ t ≠ y max ( 0 , 1 + w y ^ x − w y x )

其中， wŷ x+b w y ^ x + b 表示错误的分类器预测值， wyx+b w y x + b 表示正确的分类器预测值， 1 1 表示分类阈值。
如下图SVM的预测结果所示：

图片来源：CS231n 2016 通关 第三章-SVM与Softmax

运用公式1：
x1 x 1 的Hinge loss

ℓ(y)=max(0,1+5.1−3.2)=2.9 ℓ ( y ) = max ( 0 , 1 + 5.1 − 3.2 ) = 2.9

x2 x 2 的Hinge loss

ℓ(y)=max(0,1+2.0−4.9)=0 ℓ ( y ) = max ( 0 , 1 + 2.0 − 4.9 ) = 0

x3 x 3 的Hinge loss

ℓ(y)=max(0,1+2.5−(−3.1))=6.6 ℓ ( y ) = max ( 0 , 1 + 2.5 − ( − 3.1 ) ) = 6.6

则 L=13∑3i(2.9+0+6.6) L = 1 3 ∑ i 3 ( 2.9 + 0 + 6.6 )

运用公式2：
也差不多，最后的结果是 2.9,0,10.9 2.9 , 0 , 10.9 ，然后再求平均。PS: 公式2在实际中应用更多。

SSVM

  Hinge loss的变体也被应用于Structured SVMs中。这里不太懂…

优化

  Hinge loss是一个凸函数(convex function)，所以适用所有的机器学习凸优化方法。
虽然Hinge loss函数不可微，但我们可以求它的分段梯度：

∂ℓ∂wi={−t⋅xi0if t⋅y<1otherwise ∂ ℓ ∂ w i = { − t ⋅ x i if  t ⋅ y < 1 0 otherwise

当然，Hinge loss的梯度在 ty=1 t y = 1 点处未定义。

平滑

  为了解决Hinge loss的优化问题，现在有两种平滑(smoothed)策略：

ℓ(y)=⎧⎩⎨⎪⎪12−ty12(1−ty)20if  ty≤0,if  0<ty≤1,if  1≤ty ℓ ( y ) = { 1 2 − t y if     t y ≤ 0 , 1 2 ( 1 − t y ) 2 if     0 < t y ≤ 1 , 0 if     1 ≤ t y

ℓ(y)=12γmax(0,1−ty)2 ℓ ( y ) = 1 2 γ max ( 0 , 1 − t y ) 2

其中通常取 γ=2 γ = 2