【原文翻译】Multi-Agent Pathfinding: Definitions, Variants, and Benchmarks

Multi-Agent Pathfinding: Definitions, Variants, and Benchmarks

Abstract

多智能体寻路（MAPF）问题是为多个智能体规划路径的基本问题，其中的关键约束条件是智能体能够同时沿着这些路径前进，而不会相互碰撞。MAPF 的应用包括自动仓库和自动驾驶汽车。在过去几年中，有关 MAPF 的研究一直在蓬勃发展。不同的 MAPF 研究论文做出了不同的假设，例如，智能体是否能同时穿越同一条道路，并具有不同的目标函数，例如，最小化时间跨度或智能体行动成本总和。这些假设和目标有时是隐含假设或非正式描述。这就很难在研究论文中建立适当的比较基线，也使实践者很难找到与其具体应用相关的论文。本文旨在填补这一空白，为研究人员和从业人员提供支持，为描述常见的 MAPF 假设和目标提供统一的术语。此外，我们还提供了两个 MAPF 基准的指针。特别是，我们为 MAPF 引入了一个新的基于栅格的基准，并通过实验证明它对当代 MAPF 算法构成了挑战。

1 Introduction

MAPF 是多智能体规划问题的一种重要类型，其任务是为多个智能体规划路径，其中的关键约束条件是这些智能体能够同时沿着这些路径前进而不会相互碰撞。MAPF 在当代有一系列相关应用，包括自动仓库、自动驾驶汽车和机器人。因此，近年来这一问题受到了各研究小组和学术界的关注（Standley，2010 年；Felner 等，2017 年；Surynek 等，2016 年；Bart ́ ak、ˇ Svancara 和 Vlk，2018 年；Cohen 等，2018a；Li 等，2019 年；Ma 等，2019a）。

不同的 MAPF 研究论文考虑了不同的智能体假设，旨在实现不同的目标。这些假设和目标有时是隐含的，有时是非正式描述的。即使在对假设和目标函数进行正式描述的情况下，所使用的 MAPF 术语仍然存在差异。这就很难浏览和理解现有文献，也很难建立适当的比较基线。此外，从业人员也很难找到与其具体应用相关的论文。

本文旨在通过引入统一术语来描述 MAPF 问题，并建立用于评估 MAPF 算法的通用基准和评估措施，来应对这一日益严峻的挑战。本文提出的统一 MAPF 术语是我们对目前研究的 MAPF 变体进行分类的尝试。我们希望这一术语能成为未来研究人员的共同基础，并被他们用来简洁准确地描述自己的贡献。

在本文的第二部分，我们向社区介绍了一种新的栅格 MAPF 基准。该基准包括一组不同的地图以及生成的源顶点和目标顶点。我们报告了标准 MAPF 算法在该基准上的性能，作为未来研究的比较基准。该基准旨在帮助未来的研究人员，对现有和未来的 MAPF 算法进行更科学严谨的实证比较。我们并不声称这些基准是完美的，因为它们可能存在一些偏差。但是，通过使用和研究，我们可以发现并纠正这些偏差。同样重要的是要强调，本文无意成为对最先进 MAPF 算法的调查。有关此类调查，请参见（Felner 等人，2017 年；Ma 和 Koenig，2017 年）。此外，新创建的网站 http://mapf.info 包含与 MAPF 相关的教程和其他资源。

2 Classical MAPF

我们首先描述一个经典的 MAPF 问题。有 k 个智能体的经典 MAPF 问题的输入是一个元组 $〈G,s,t〉$，其中 $G=(V,E)$ 是一个无向图，$s:[1,...,k]\to V$ 将一个智能体映射到一个源顶点，$t:[1,...,k]\to V$ 将一个智能体映射到一个目标顶点。假定时间是离散的，在每个时间步中，每个智能体都位于图顶点中的一个，并可以执行一个动作。经典 MAPF 中的动作是一个函数 $a:V\to V,a(v)=v^{\prime }$ 表示如果一个智能体位于顶点 v 并执行了 a，那么在下一个时间步中它将位于顶点 $v\prime$。每个智能体都有两种行动：等待和移动。等待行动是指智能体在下一个时间步停留在当前顶点。移动动作意味着智能体从当前顶点 v 移动到图中相邻的顶点 $v\prime (i.e(v,v\prime )\in E)$。

对于一个行动序列 $\pi =(a1,...an)$ 和一个智能体 $i$，我们用 ${\pi }_i[x]$ 表示从智能体的源 $s(i)$ 出发，执行完 $\pi$ 中前 $x$ 个行动后智能体的位置。形式上，${\pi }_i[x]=a_x(a_{x-1}(...a_1(s(i))))$。如果在 $s(i)$ 中执行该行动序列的结果是处于 $t(i)$，即如果 ${\pi }_i[|\pi |]=t(i)$，那么行动序列 $\pi$ 就是智能体 $i$ 的单个智能体计划。解决方案是一组 k 个智能体规划，每个智能体一个规划。

2.1 Types of Conflicts in Classical MAPF

MAPF 求解器的首要目标是找到一个解决方案，即每个智能体的单个智能体规划，该规划可以在不发生冲突的情况下执行。为了实现这一目标，MAPF 求解器在规划过程中使用了冲突的概念，如果任意两个智能体计划之间不存在冲突，则称 MAPF 解决方案有效。冲突的定义取决于环境，相应地，经典 MAPF 文献中也包含了几种不同的冲突定义。下面我们将列出常见的冲突定义。设 ${\pi }_i$ 和 ${\pi }_j$ 是一对智能体规划。

• 顶点冲突 如果根据这些规划，智能体计划在同一时间步占据相同的顶点，那么${\pi }_i$和 ${\pi }_j$ 之间就会发生顶点冲突。从形式上看，如果存在一个时间步 x，使得 ${\pi }_i[x]={\pi }_j[x]$ ，那么 πi 和 πj 之间就会发生顶点冲突。
• 边冲突 如果根据这些规划，智能体计划在同一时间步长沿同一方向穿越同一条边，那么${\pi }_i$ 和 ${\pi }_j$ 之间就会发生边冲突。从形式上看，如果存在一个时间步 $x$，使得 ${\pi }_i[x]={\pi }_j[x]$ 和 ${\pi }_i[x+1]={\pi }_j[x+1]$ ，那么 ${\pi }_i$ 和 ${\pi }_j$ 之间就存在边缘冲突。
• 跟随冲突 如果一个智能体计划占据另一个智能体在前一时间步中占据的顶点，则 ${\pi }_i$ 和 ${\pi }_j$ 之间发生跟随冲突。从形式上看，如果存在一个时间步 $x$，使得 ${\pi }_i[x+1]={\pi }_j[x]$ ，那么 ${\pi }_i$ 和 ${\pi }_j$ 之间就存在跟随冲突。
• 循环冲突 如果在同一时间步中，每个智能体都移动到之前被另一个智能体占据的顶点，形成 "旋转循环 "模式，那么一组单一智能体规划 ${\pi }_i,{\pi }_{i+1},...{\pi }_j$ 之间就会发生循环冲突。从形式上看，如果存在一个时间步 $x$，其中 ${\pi }_i(x+1)={\pi }_{i+1}(x)，{\pi }_{i+1}(x+1)={\pi }_{i+2}(x)$…且 ${\pi }_{j-1}(x+1)={\pi }_j(x)$和 ${\pi }_j(x+1)={\pi }_i(x)$，则一组规划 ${\pi }_i,{\pi }_{i+1},...{\pi }_j$ 之间会发生循环冲突。
• 交换冲突 如果智能体计划在一个时间步内交换位置，则 ${\pi }_i$ 和 $p{i}_j$ 之间会发生交换冲突。从形式上看，如果存在一个时间步 $x$，使得 ${\pi }_i[x+1]={\pi }_j[x]$ 和 ${\pi }_j[x+1]={\pi }_i[x]$ ，那么 ${\pi }_i$ 和 ${\pi }_j$ 之间就存在交换冲突。在目前的 MAPF 文献中，这种冲突有时被称为边缘冲突。

图 1 展示了不同类型的冲突。请注意，上述冲突定义集肯定不是所有可能冲突的完整集合。考虑到这些冲突的形式定义，它们之间显然存在支配关系：（1）禁止顶点冲突意味着也禁止边冲突；（2）禁止跟随冲突意味着也禁止循环冲突和交换冲突；（3）禁止循环冲突意味着也禁止交换冲突。反之亦然，(1) 允许边冲突意味着也允许顶点冲突，(2) 允许交换冲突意味着也允许循环冲突1，(3) 允许循环冲突意味着也允许跟随冲突。

要正确定义一个经典的 MAPF 问题，我们需要指定解决方案中允许哪些类型的冲突。最少的限制是只禁止边冲突。然而，据我们所知，之前所有关于经典 MAPF 的研究都禁止顶点冲突。一些关于带有效载荷传输的 MAPF 的研究允许交换冲突（Ma 等人，2016 年）。大多数基于搜索的 MAPF 算法（Standley，2010 年；Felner 等，2017 年）禁止交换冲突，但允许跟随冲突。一些关于基于编译的 MAPF 算法的研究，以及所有将 MAPF 视为卵石运动问题的研究，也都禁止跟随冲突（Surynek 等人，2016 年；Bart ́ ak 等人，2017 年）。

2.2 Agent Behavior at Target in Classical MAPF

在经典 MAPF 问题的解法中，智能体可能会在不同的时间步达到目标。因此，在定义经典 MAPF 问题时，必须定义智能体在到达目标后和最后一个智能体到达目标前的时间步中的行为方式。

对于智能体在目标处的行为方式，有两种常见的假设。

• 停留在目标位置(Stay at target) 在此假设下，一个智能体在其目标位置等待，直到所有智能体都到达目标位置。这个等待的智能体将会与任何在它到达目标后经过其目标的规划产生顶点冲突。从形式上看，在停留在目标假设下，如果存在一个时间步长 $t\ge |{\pi }_i|$ ，使得 ${\pi }_j[t]={\pi }_i[|{\pi }_i|]$ ，那么一对智能体规划 ${\pi }_i$ 和 ${\pi }_j$ 将发生顶点冲突。
• 在目标处消失(Disappear at target) 根据这一假设，当一个智能体到达目标处时，它会立即消失。这意味着在相应智能体到达目标的时间步之后，该智能体的规划将不会有任何冲突。

之前关于经典 MAPF 的研究大多假设目标停留，但最近的研究也考虑了目标消失假设（Ma 等人，2019a）。

2.3 Objective Functions in Classical MAPF

可以说，在 MAPF 的大多数实际应用中，一些 MAPF 解决方案比其他解决方案更好。为了把握这一点，经典 MAPF 的工作考虑了用于评估 MAPF 解决方案的目标函数。在经典 MAPF 中，用于评估解决方案的两个最常用的函数是时间跨度（makespan）和成本总和（sum of costs）。

• 时间跨度(Makespan) 所有智能体到达目标所需的时间步数。对于 MAPF 解决方案 $\pi =\{{\pi }_1,...{\pi }_k\}$ 的 Makepan 定义为 $ma{x}_{1\le i\le k}|{\pi }_i|$。
• 成本总和 每个智能体到达目标所需的时间步骤总和。$\pi$ 的成本总和定义为 ${\sum }_{1\le i\le k}|{\pi }_i|$。成本总和也称为流动时间。

如果智能体在目标处的行为是停留在目标处，而目标函数是成本总和，那么就需要说明停留在目标处会如何影响成本总和。例如，我们可以定义，如果智能体在目标处等待，那么它不会增加成本总和。大多数前期工作的共同假设是，除非智能体不打算再次远离目标，否则停留在目标地就算是等待行动。例如，假设智能体 $i$ 在时间步长 $t$ 到达目标，在时间步长 $t\prime$ 离开目标，在时间步长 $t\prime \prime$ 回到目标，然后停留在目标，直到所有智能体都到达目标。那么，这个单智能体规划将对相应解的成本总和贡献 $t\prime \prime$。

我们并不声称这些是经典 MAPF 唯一可能的目标函数。我们还可以定义其他目标函数，例如到达目标所需的非等待行动总数（有人称之为燃料总和），以及智能体不在目标中花费的总时间。不过，据我们所知，上述目标函数是经典 MAPF 先前研究中使用的唯一目标函数。基于编译的 MAPF 算法广泛使用了时间跨度，而大多数基于搜索的 MAPF 算法则使用了成本总和。不过，两种类型的 MAPF 算法也都曾使用过这两种目标函数（Surynek 等人，2016 年）。此外，还有人研究如何在给定的 makespan（即截止时间）内最大化达到目标的智能体数量（Ma 等人，2018 年）。

3 Beyond Classical MAPF

上述所有经典 MAPF 变体都有如下假设：(1) 时间被离散化为一个个时间步；(2) 每个行动正好需要一个时间步；(3) 在每个时间步中，每个智能体正好占据一个顶点。接下来，我们将简要列出几种放宽这些假设的 MAPF 变体。

3.1 MAPF on Weighted Graphs

假设每个动作–移动或等待–正好需要一个时间步长，这就隐含地假设了智能体的运动模型有些简单。MAPF 文献中研究了更复杂的运动模型，其中不同的行动可能有不同的持续时间。这意味着表示智能体可能占据的位置的底层图（前面用 G 表示）现在是一个加权图，其中每条边的权重代表智能体穿越这条边所需的时间。

Bartak 等人（2018 年）提出了一种基于调度的加权图 MAPF 方法，Walker 等人（2018 年）提出了一种递增成本树搜索（ICTS）算法的变体。Yakovlev 和 Andreychuk（2017）提出了针对加权图的 SIPP 算法（Phillips 和 Likhachev，2011 年）和优先级规划的混合算法。

迄今为止，用于 MAPF 研究的加权图类型包括：

• MAPF in $k^2$-neighbor grids 这种映射是加权图的一种受限形式，其中每个顶点代表二维栅格中的一个单元格。一个智能体在一个单元格中的移动行动是其所有 $k^2 $个相邻单元格，其中 k 是一个参数。成本基于欧氏距离，因此当 k>2 时，会产生不同成本的行动。例如，在一个 8 个相邻单元的栅格中，对角线移动的成本为 √2，而向其中一个红心方向移动的成本为 1。图 2 显示了 k =2、3、4 和 5 时 2k 个邻居栅格中可能的移动行动。

• 欧几里得空间中的 MAPF(MAPF in Euclidean space) 欧几里得空间中的 MAPF 是 MAPF 的一般化，其中 G 中的每个节点都代表一个欧几里得点（x，y），边代表允许的移动操作。例如，当底层图是为连续欧氏环境生成的路线图时，就会出现这种设置（Khatib，1986 年；Wagner、Kang 和 Choset，2012 年）。

3.2 Feasibility Rules

经典 MAPF 中使用的 "无冲突 "有效解决方案的定义只是解决方案要求的一种。我们使用 "可行性规则 "一词来指对 MAPF 解决方案的要求。还有人提出了其他 MAPF 可行性规则。

• 鲁棒性规则(Robustness rules)：这些规则旨在确保 MAPF 解决方案考虑到执行中的意外延迟。k-robust MAPF 规划为智能体建立了足够的缓冲区，使其在不导致冲突的情况下被延迟到 k 个时间步（Atzmon 等人，2018 年）。当未来延迟的概率已知时，鲁棒性规则可以要求智能体在执行过程中发生冲突的概率低于给定的约束（Wagner 和 Choset，2017 年），或者与执行策略相结合以保证无冲突执行（Ma、Kumar 和 Koenig，2017 年）。

• 编队规则(Formation rules)。这些是对智能体允许的移动行动的限制，取决于其他智能体的位置，但与碰撞无关。例如，限制智能体保持指定队形（Barel、Manor 和 Bruckstein，2017 年），或与一组相邻智能体保持通信联系（Stump 等，2011 年；Gilboa、Meisels 和 Felner，2006 年）。

3.3 From Pathfinding to Motion Planning

在经典的 MAPF 中，智能体被假定只占据一个顶点，从某种意义上说，没有体积，没有形状，并且以恒定的速度移动。相比之下，运动规划算法直接考虑了这些特性。在这里，智能体在每个时间步都位于一个配置中，而不仅仅是一个顶点，其中配置指定了智能体的位置、方向、速度等，而配置之间的边代表了运动学运动。一些著名的 MAPF 变体正在逐步缩小经典 MAPF 与运动规划之间的差距。

• 大型智能体的 MAPF(MAPF with large agents.)。一些 MAPF 研究考虑了具有特定几何形状和体积的智能体（Li 等人，2019 年；Walker、Sturtevant 和 Felner，2018 年；Yakovlev 和 Andreychuk，2017 年；Thomas、Deodhare 和 Murty，2015 年）。智能体有体积这一事实提出了它们在底层图 G 中的位置以及如何在其中移动的问题。特别是，如果一个智能体位于一个顶点，它可能会禁止其他智能体占据附近的顶点。同样，如果一个智能体沿着一条边移动，它可能会禁止其他智能体沿着相交的边移动或停留在离边太近的顶点。这可能会引入新类型的冲突，如顶点到顶点、边到边和边到顶点的冲突（H ̈ onig 等人，2018 年）。

文献中出现了几种求解具有大型智能体的 MAPF 的方法，包括基于 CBS 的方法（Li 等人，2019 年）、基于 ICTS 的方法（Walker、Sturtevant 和 Felner，2018 年）以及优先规划方法（Yakovlev 和 Andreychuk，2017 年）。具有体积的智能体的一个特例是车队设置，其中智能体占据一串顶点及其连接边（Thomas、Deodhare 和 Murty，2015 年）。

• 具有运动学约束的 MAPF(MAPF with kinematic constraints) 其他 MAPF 研究考虑了智能体移动动作的运动学约束（H ̈ onig 等人，2017 年；Walker、Chan 和 Sturtevant，2017 年）。也就是说，智能体可以执行的移动动作不仅取决于其当前位置，还取决于速度和方向等状态参数。这种约束的一个副产品就是底层图变成了有向图，因为由于智能体的运动学约束，可能有一些边只能在一个方向上通过。例如，MAPF-POST 就是一种 MAPF 算法，它通过对 MAPF 算法创建的解决方案进行后处理，来考虑这些运动学约束。还有一种基于还原的方法，假定旋转动作是运动学约束的一半（Bart ́ ak 等人，2018 年）。

3.4 Tasks and Agents

在经典的 MAPF 中，每个智能体只有一个任务，即把它送到目标地点。在 MAPF 文献中，已经进行了一些扩展，其中智能体可以被分配多个目标。

• 匿名 MAPF(Anonymous MAPF) 在这个 MAPF 变体中，目标是将智能体移动到一组目标顶点，但哪个智能体到达哪个目标并不重要（Kloder 和 Hutchinson，2006 年；Yu 和 LaValle，2013 年）。另一种将这种 MAPF 变体视为 MAPF 问题的方法是，每个智能体都可以被分配到任何目标，但必须是智能体和目标之间的一一映射。
• 彩色 MAPF(Colored MAPF) 这种 MAPF 变体是匿名 MAPF 的广义化，其中将智能体分组为团队，每个团队都有一组目标。目标是将每个团队中的智能体移动到它们的目标处（Ma 和 Koenig，2016 年；Solovey 和 Halperin，2014 年）。另一种将这种 MAPF 变体视为 MAPF 问题的方法是，每个智能体只能从为其团队指定的目标集合中分配目标。我们可以将彩色 MAPF 进一步推广，将一个目标和一个智能体分配给多个团队。
• 在线 MAPF(Online MAPF) 在在线 MAPF 中，一连串的 MAPF 问题是在同一个图上求解的。这种设置也被称为 “终身 MAPF”（Ma 等人，2017 年；2019b）。在线 MAPF 问题可分为以下几类。
  • 仓库模型(Warehouse model)。这是由一组固定的智能体解决 MAPF 问题的设置，但在一个智能体找到一个目标后，它可能会被委派去不同的目标（Ma 等人，2019b）。这种设置受到了自主仓库 MAPF 的启发。
  • 交叉模型(Intersection model.) 这是新智能体可能出现的环境，每个智能体只有一个任务–到达目标（ˇ Svancara et al. 2019）。这种情况的灵感来自于自动驾驶车辆进出交叉路口（Dresner 和 Stone，2008 年）。

当然，在混合模型中，智能体在到达目标后可以接受新的任务，新的智能体也可以随着时间的推移而出现，这也是可能的。

4 Benchmarks

在本节中，我们将介绍如何对经典 MAPF 算法进行评估，为此提出一个有组织的基准，并指出其他相关的基准套件。

4.1 Characteristics of a MAPF Benchmark

MAPF 问题由一个图形和一组源顶点和目标顶点定义。因此，MAPF 的基准包括一组图形，以及每个图形的一组源顶点和目标顶点。

用于评估 MAPF 算法的图 以往工作中常用的地图类型包括：

• Dragon Age Origins (DAO) maps 这些栅格取自游戏《龙腾世纪起源》，可在 Sturtevant 的 movingai.com 储存库中公开获取（Sturtevant，2012 年）。这些栅格相对较大且开放，其中一些栅格大到 1000 × 1000 甚至更大。
• 开放式 N × N 栅格(Open N × N grids) 这些网格为 N×N 网格，其中常见的 N 值为 8、16 和 32。这种栅格允许进行智能体与空间比例或智能体密度较高的实验，其中没有智能体的顶点较少。
• 带有随机障碍物的 N × N 栅格(N × N grids with random obstacles) 这些栅格为 N×N 栅格，其中一组栅格单元被随机选中，并被认为是无法通过的（障碍物）（Standley，2010 年）。
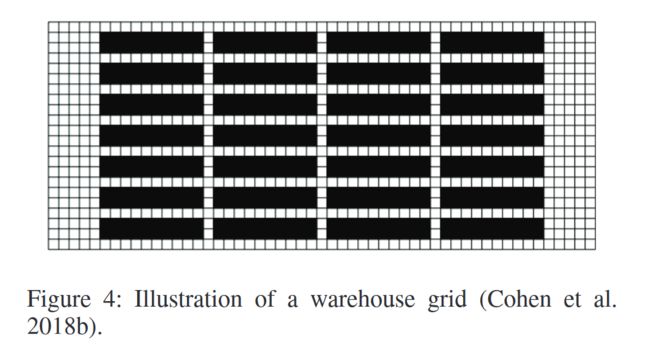
• 仓库栅格(Warehouse grids) 受现实世界中自主仓库应用的启发，最近的 MAPF 论文还尝试了形状类似于自动化仓库的栅格，其中有长长的走廊（Ma 等人，2017 年；Cohen 等人，2018a）。图 4 显示的是一个仓库栅格的图示（Cohen 等人，2018a）。

4.2 Sources and targets assignments

选择地图类型后，需要设置智能体的源顶点和目标顶点。文献中使用了多种方法来设置智能体的源顶点和目标顶点，其中包括

• 随机 通过随机选择顶点来设置源顶点和目标顶点，并确保它们之间在图形中存在路径。
• 聚类 在图中随机选择顶点，设置第一个智能体的来源和目标。将所有其他智能体的来源和目标分别设置为与第一个智能体的来源和目标的距离最多为 $r$，其中 $r$ 是一个参数。
• 指定 通过从指定的一组可能的源顶点中随机选择来设置每个智能体的源，并通过从一组指定的可能的目标顶点中选择来类似地设置每个智能体的目标。

随机分配可能是文献中最常见的方法。聚类分配法的使用使 MAPF 问题更具挑战性。指定分配法已在先前的工作中用于模拟自动化仓库（Cohen、Uras 和 Koenig，2015 年；Ma 等人，2019a；2019b）和交叉路口的自动驾驶车辆（ˇ Svancara 等人，2019 年）。在自动化仓库中，通常会有人类在特定位置对交付的垃圾箱进行包装，大多数任务都是将包裹交付给这些位置的人类，或从人类手中取回包裹。在自动驾驶车辆驶入和驶出交叉路口的情况下，指定的来源和目标就是交叉路口的终点（ˇ Svancara 等人，2019 年）。

4.3 Publicly Available MAPF Benchmarks

我们在此介绍两个公开的 MAPF 研究基准，其中第一个是本文首次介绍的新基准集。

基于栅格的 MAPF 这一公开4 基准由 24 幅地图组成，这些地图分别来自：（1）真实城市地图；（2）视频游戏《龙腾世纪起源》和《龙腾世纪 2》；（3）有随机障碍物和无随机障碍物的开放栅格；（4）类似迷宫的栅格；以及（5）类似房间的栅格。所有地图均来自 MovingAI 寻路资源库（Sturtevant，2012 年）5。图 5 显示了上述每种类型的地图示例，表 1 显示了这些地图的尺寸。

每张地图有 25 个场景。每个场景都有一个源顶点和目标顶点列表，这些顶点是用随机方法的变体设置的（见第 4.2 节）。每个地图最大可达区域内的所有点都是随机配对的，然后将前 1000 个问题放入场景中。因此，我们可以通过选择任意的源顶点和目标顶点子集，从每个场景中创建一组 MAPF 问题。

我们建议按以下方式使用该基准。对于选定的 MAPF 算法、地图类型和场景，尝试在每个场景中解决尽可能多的智能体问题，按连续顺序添加。也就是说，从创建两个智能体的 MAPF 问题开始，使用与所选场景相关的前两个源-目标对，并运行所选的 MAPF 算法来解决这个问题。如果所选算法在合理的时间内成功解决了这个 MAPF 问题，则使用该方案的前三个源-目标对创建一个包含 3 个智能体的新 MAPF 问题，并尝试使用所选 MAPF 算法解决该问题。如此反复进行，直到所选算法无法在合理时间内解决所创建的 MAPF 问题。然后，经过评估的算法就可以报告其在合理时间内能够解决的每个场景的最大智能体数量。

为了提供一个比较基线，我们使用 ICBS（Boyarski 等人，2015 年）执行了这一评估过程。使用本文介绍的术语，我们的设置是在 4 邻网格上的经典 MAPF 设置，其中：（1）禁止边、顶点和交换冲突；（2）允许跟随和循环冲突；（3）目标是成本之和；（4）智能体在目标处的行为是停留在目标处。

表 1 显示了评估结果。我们将运行时间限制为 30 秒。不同的行对应不同的地图。大小 "列显示了每个地图的行数和列数。问题 "列报告了每个地图中可用问题的数量。请注意，这个数字是 25 个方案的总和，其中一个方案中可用问题的数量就是为其定义的源-目标对的数量。已解决 "一栏报告的是 ICBS 在指定时限（30 秒）内解决的问题数量。可以看出，虽然 ICBS 能够解决很多问题，但该基准中的问题足够复杂，因此 ICBS 无法在规定时间内解决很多问题。因此，这个栅格 MAPF 基准中的问题难度足以对当代 MAPF 求解器构成挑战。

表 1 增加了两列–"最小 "和 “最大”。这两列报告了 ICBS 在该数字最小（“Min”）和最大（“Max”）时所解决的最大智能体数量。例如，地图 brc202d 的 "最小 "值为 2，"最大 "值为 22。这意味着该地图存在这样一种情况，即 ICBS 在超时前最多只能解决 2 个智能体的问题，而该地图也存在另一种情况，即 ICBS 最多能解决 22 个智能体的问题。我们报告这些数值是为了显示同一张地图不同场景之间的难度差异。

Asprilo 对 MAPF 研究有用的另一个工具是 Asprilo。Asprilo 是一个用于模拟自动化仓库的公开可用框架（Gebser 等人，2018 年）。它包括用于定义和生成标准自动化仓库规划问题的工具，以及用于验证和可视化解决这些问题的规划的工具。

Asprilo 支持的规划问题类型包括机器人在仓库中拾取并将箱子从一个地方运送到另一个地方的问题。这些场景被分为不同的领域，代表不同类型的问题。MAPF 社区特别感兴趣的是领域 M，它基本上代表了 MAPF 问题。因此，我们可以将该领域的问题作为 MAPF 算法的基准。图 6 显示了来自 Asprilo 的两个场景。左侧的场景是一个完整的仓库场景，智能体的任务是将箱子从一个地方移到另一个地方。右侧的场景是一个纯移动场景，即经典的 MAPF 问题。有关 ASPRILO 的详细信息，请参阅（Gebser 等人，2018 年）以及该项目的网站。

5 Conclusion

在本文的第一部分，我们定义了 "经典 "多智能体寻路（MAPF）问题中的常见假设，并讨论了它们之间的关系。然后，我们定义了之前发表的经典 MAPF 的显著扩展。在本文的第二部分，我们介绍了一套新的 MAPF 基准问题，并指出了另一套 MAPF 基准问题。本文的两个部分都旨在为 MAPF 研究提出一种通用语言、术语和实验环境。我们希望未来的 MAPF 研究人员能够遵循我们的术语，并发现这些基准是有用的。