【 顺序表经典算法—移除元素和合并两个有序数组】

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

目录

前言

经典算法OJ题1： 移除元素

解法一、逐个判断

解法二、双指针覆盖

经典算法OJ题2： 合并两个有序数组

OJ题分为两个类型：

总结

---

前言

世上有两种耀眼的光芒，一种是正在升起的太阳，一种是正在努力学习编程的你!一个爱学编程的人。各位看官，我衷心的希望这篇博客能对你们有所帮助，同时也希望各位看官能对我的文章给与点评，希望我们能够携手共同促进进步，在编程的道路上越走越远!

---

提示：以下是本篇文章正文内容，下面案例可供参考

经典算法OJ题1： 移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

首先要想清楚移除的本质并不是真删除，而是把元素覆盖即可，覆盖n个元素后，数组总长度就要-n

解法一、逐个判断

把数组从头开始遍历，找到目标元素val，就执行一次任意位置删除

注意： 在实际写代码时，每删除一次元素，i 都要回退一次，因为有的测试用例是 3 3 3 3，val = 3，如果不回退，直接覆盖，会少删两个元素。

代码演示:

void Erase(int* nums, int pos, int len)
{
	assert(len > 0);
	while (pos < len)
	{
		nums[pos] = nums[pos + 1];//数组中后面的数据把前面的数据覆盖
		pos++;//向后移动
	}
}
int removeElement(int* nums, int numsSize, int val)
{
	assert(nums);  //nums不能为空指针
	int i = 0;
	int len = numsSize;//数组的有效元素个数
	for (i = 0; i < len; i++)
	{
		if (nums[i] == val)
		{
			Erase(nums, i, len);
			i--;//这里i--是因为后面的值把i所在的位置覆盖，
			    //如果不--，出了这个循环，i++, 就会把再i上赋的值给忽略，少判断一次
			len--;
		}
	}
	return len;//返回的是删除之后的数组长度
}

解法二、双指针覆盖

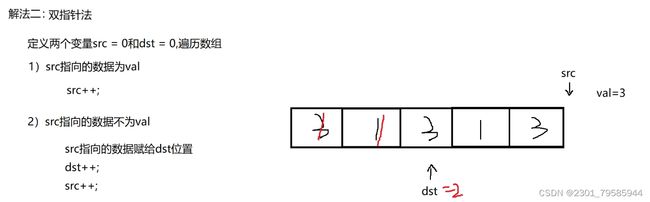
这是一种比较巧妙的解法，用到了双指针 ，对数组内元素进行覆盖，具体实现为：存在两个指针src 、dst ，两者初始都指向数组起始位置，遍历 整个数组，对指针 src 和指针 dst 所指向的值进行比较，如果 *src != val ，就把 *src 赋给 *dst ，然后 dst 向后移动，当然无论相等还是不相等，src 都需要往后移动，这个解法的目的就是把数组中所有非目标值的元素往前移动，最后返回 dst 的下标（dst的下标就是数组中不等于 val 的值的个数）

代码演示：

int removeElement(int* nums, int numsSize, int val) {
    int src = 0;
    int dst = 0;
    while (src < numsSize)
    {
        if (nums[src] == val)
        {
            src++;
        }
        else
        {
            nums[dst] = nums[src];
            dst++;
            src++;
        }
    }
    return dst;
}

经典算法OJ题2： 合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

nums1

数组	1	2	3	0	0	0
下标	0	1	2	3	4	5

nums2

数组	2	5	6
下标	0	1	2

假设比小的思路：设L1为nums1数组的起始位置，L2为nums2数组的起始位置，我们从比小的角度看，L1为1时，L2为2，L2大；L1++，此时L1为2，L2为2，我们假设还是L1的2大；L1++，此时L1为3，L2为2，我们把L2的值赋给L1，那么原来L1位置上的3就没了，所以这种比小的思路是不行的。

假设比大的思路：设L1为nums1数组实际有效数据的最后一个元素（下标为2），L3为nums1数组初始化的最后一个位置（下标为5）；L2为nums2数组的最后一个元素；L2为6时，L1为3，L2赋值给L3，L2--,L3--，L2不变;L2为5时，L1为3，L2赋值给L3，L2--,L3--，L1不变;L2为2时，L1为3，此时L1赋值给L3，L3--,L1--;L2为2，L1为2，假设L2的2比L1的2要大，L2赋值给L3，L3--,L2--;此时L2已经完成循环，所以比大的思路时正确的。

此外，我们仍需要考虑两种情况：L2先出循环和L1先出循环。

上面的比大思路就是我们的L2先出循环，没有是什么好考虑的。

我们来看L1先出循环的情况：

nums1

数组	4	5	6	0	0	0
下标	0	1	2	3	4	5

nums2

数组	1	2	3
下标	0	1	2

仍然是比大的思路：L2为3时，L1为6，L1的值赋给L3，L1--,L3--,L2不变；L2为3时，L1为5，L1的值赋给L3，L3--,L1--,L2不变；L1为4时，L2为3，L1的值赋给L3，L3--,L1--,L2不变；此时L1先完成循环，但是L2的数据还在原位，因为都是递增的排序，那么只需要把L2数组的元素赋值给L3中。

代码演示：

void merge(int* nums1, int m, int* nums2, int n) 
{
    int l1 = m - 1, l2 = n - 1;
    int l3 = m + n - 1;
    while (l1 >= 0 && l2 >= 0)
    {
        if (nums1[l1] > nums2[l2])
        {
            nums1[l3] = nums1[l1];
            l1--;
            l3--;
        }
        else
        {
            nums1[l3] = nums2[l2];
            l3--;
            l2--;
        }
    }
    while (l2 >= 0)
    {
        nums1[l3] = nums2[l2];
        l3--;
        l2--;
    }
}

OJ题分为两个类型：

1：接口型（不需要main()函数，我们把代码提交之后，后端会自动拼接main()函数）

2：IO型（需要main()函数）

---

总结

好了，本篇博客到这里就结束了，如果有更好的观点，请及时留言，我会认真观看并学习。
不积硅步，无以至千里；不积小流，无以成江海。