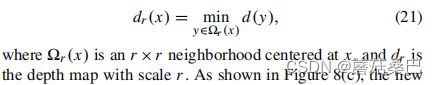【文献阅读】A Fast Single Image Haze Removal Algorithm Using Color Attenuation Prior——图像去雾

目录

1. 摘要

2. 引言

2.1 背景 

2.2 相关工作

2.3 提出方法

3. 大气散射模型

4. 颜色衰减先验

5. 场景深度恢复

5.1 线性模型定义

5.2 收集训练数据集

5.3 学习策略

5.4 深度信息估计

6. 场景亮度恢复

6.1 大气光估计

6.2 场景亮度恢复

7. 实验

7.1 参数设置

7.2 定性比较

7.3 定量比较

7.3.1 耗时比较

7.4.2 MSE指标比较

7.4.3 SSIM指标比较

8. 结论

---

1. 摘要

单幅图像的雾霾去除一直是一个具有挑战性的问题，由于它ill-posed性质。

在本文中，我们提出了一种颜色衰减先验方法，用于从单输入模糊图像中去除雾。在该先验条件下，通过建立线性模型对模糊图像的场景深度进行建模，并采用监督学习的方法对模型参数进行学习，可以很好地恢复图像的深度信息。有了雾霾图像的深度图，我们可以很容易地通过大气散射模型估计散射和恢复场景的亮度，从而有效地从单幅图像中去除雾霾。实验结果表明，该方法在效率和除雾效果方面都优于目前最先进的除雾算法。

2. 引言

2.1 背景 

坏天气下拍摄的户外照片，常常会损失对比度和保真度，这是由于光在传播过程中被大气中的颗粒、水滴等浑浊介质吸收和散射造成的。此外，大多数依赖于输入图像清晰度的自动系统由于图像的退化而无法正常工作。因此，改进图像去雾技术将有利于许多图像理解和计算机视觉应用

2.2 相关工作

· 早期研究者使用传统图像处理技术来做单张图像去雾，例如实例，基于直方图的除雾方法，然而，由于单一的模糊图像很难提供太多的信息，因此除雾效果是有限的。

· 后来，研究人员尝试用多幅图像来提高去雾性能。在[18]-[20]中，使用基于偏振的方法对不同偏振度的多幅图像进行除雾。在[21]-[23]中，Narasimhan等人提出了不同天气条件下同一场景的多幅图像去霾方法。在[24]和[25]中，根据给定的深度信息进行除雾。

· 近年来，基于物理模型的单幅图像去雾研究取得了重大进展。在无雾图像的局部对比度远高于有雾图像的假设下，Tan[26]提出了一种基于马尔可夫随机场(Markov Random Field, MRF)最大化图像局部对比度的去雾方法。虽然谭的方法能够取得令人印象深刻的效果，但它往往会产生过度饱和的图像。

· Fattal[27]提出了基于独立分量分析(ICA)的彩色图像去雾方法，但该方法耗时长，不能用于灰度图像去雾。此外，在处理密集雾霾图像时也存在一些困难。

· He et al.[29]受广泛使用的暗物体减法技术[28]的启发，基于对无雾图像的大量实验，发现了暗通道先验(dark channel prior, DCP)，即在大多数非天空斑块中，至少有一个颜色通道中存在一些亮度非常低且接近于零的像素。在此前提下，他们估算了雾霾的厚度，并通过大气散射模型恢复了无雾图像。DCP方法在大多数情况下是简单有效的。然而，它不能很好地处理天空图像，并且计算量很大。

· 针对DCP算法的不足，提出了[30]-[36]、[45]-[51]等改进算法。为了提高效率，Gibson等人[31]、Yu等人[32]、He等人[43]、Tarel和Hautiere[45]、Tarel等人[46]分别用标准中值滤波、“中值滤波的中值”、引导联合双边滤波[37]-[42]和引导图像滤波代替耗时的软消光[44]。在消雾质量方面，Kratz and Nishino[48]和Nishino et al.[49]使用阶乘马尔可夫随机场对图像进行建模，以更准确地估计场景亮度;孟等人提出了一种有效的正则化去雾方法，通过探索固有的边界约束来恢复无雾图像;

· Tang等人[51]结合随机森林和四种雾相关的特征来估计散射。尽管取得了显著的进展，但最先进的方法的局限性在于所使用的与雾霾相关的先验或启发式线索不够有效或高效。

2.3 提出方法

本文提出了一种用于单幅图像去雾的彩色衰减先验算法。这个简单而强大的先验可以帮助为朦胧图像的场景深度创建一个线性模型。采用监督学习的方法学习线性模型的参数，有效地建立了模糊图像与其相应深度图之间的桥梁。利用恢复的深度信息，可以很容易地从单幅雾霾图像中去除雾霾。所提出的除雾方法的概述如图1所示。效率和去雾效果都显著优于现有去雾方法

3. 大气散射模型

大气散射模型可用如下公式表达：

这其中d是最重要的信息，因为散射系数\beta 在均匀大气条件下可视为常数[55]。此外，在理想情况下，d(x)的范围为[0，+∞)，因为图像中出现的景物可能离观察者很远，我们有:

因此，在给定阈值d_threshold的情况下，我们可以用下面的公式来估计A，而不是通过式(3)来计算大气光A

换句话说，图像中属于远视图区域的像素应该具有非常大的深度阈值。假设每个模糊图像都有一个远景，我们有:

4. 颜色衰减先验

我们发现雾霾图像中像素的亮度和饱和度随着雾霾浓度的变化变化很大。图2给出了一个自然场景的例子，显示了模糊图像中像素的亮度和饱和度是如何变化的。

如图2(d)所示，在无雾区，场景的饱和度很高，亮度适中，亮度与饱和度之差接近于零。但从图2(c)中可以看出，在雾霾的影响下，斑块的饱和度急剧下降，场景的颜色逐渐褪色，同时亮度增加，产生差值的高值。此外，从图2(b)中可以看出，在浓密的雾霾区域，我们更难识别场景的固有颜色，其差异甚至高于图2(c)。根据这一观察，在单一模糊图像中，三个属性(亮度，饱和度和差值)似乎容易有规律地变化。这是巧合，还是背后有根本原因?为了回答这个问题，我们首先回顾一下成像的过程。

成像过程如图3所示，无雾情况下成像几乎不会有任何损失。然而在有雾的情况下，雾霾天气下的成像有两种机制(直接衰减和空气光)。

一方面，由于反射能量的减少而引起的直接衰减导致了亮度的低强度。为了理解这一点，我们回顾了大气散射模型。式(1)中的项J(x)t(x)用于描述直接衰减。它揭示了这样一个事实，即图像内像素的强度将以乘法的方式减少。因此，在直接衰减的影响下，亮度有降低的趋势。

另一方面，由于环境光照的散射而形成的白色或灰色空气光，提高了亮度，降低了饱和度。我们也可以用大气散射模型来解释这一点。式(1)中最右边的项A(1−t(x))表示气流的影响。从这一项可以推断，白色或灰色气流对观测值的影响是加性的。 因此，由于空气的影响，亮度增加而饱和度降低。由于空气在大多数情况下起着更重要的作用，因此图像中的模糊区域具有高亮度和低饱和度的特点。

由于一般情况下雾霾浓度会随着场景深度的变化而增加，我们可以假设场景深度与雾霾浓度呈正相关，有:

图像中深度越深，雾越浓，差值越大

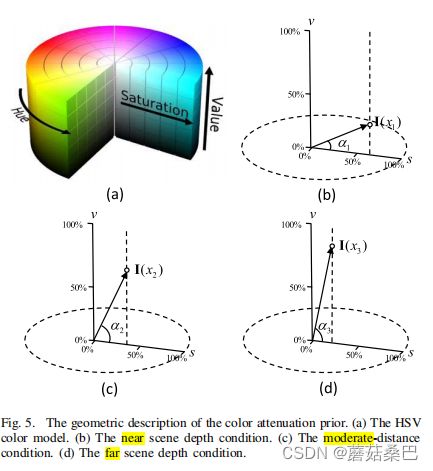
如图5所示，向量表示模糊图像,通过原点和表演我在水平面上的投影向量的向量之间的夹角和它的投影为α,根据HSV颜色模型,当α的变化介于0到90度,α的值越高,tanα的值越高,这表明更大的区别我的方向V的组件和组件的我的方向。随着深度的增加，v增大，饱和度s减小，因此α增大。也就是说，角度α与深度呈正相关。

5. 场景深度恢复

5.1 线性模型定义

深度图估计可以用如下公式表达：

（文章中有推导为什么这个深度图估计有保边特性，感兴趣的读者可以阅读原文了解）

5.2 收集训练数据集

训练数据是用来学习公式(8)中三个参数\theta_0 \theta_1 \theta_2。 我们从谷歌images和Flickr上收集无雾图像，并使用它们生成合成深度图和相应的朦胧图像，以获得足够的训练样本。生成训练样本的过程如图7所示。

· 首先，对于每个无雾图像，我们生成一个具有相同大小的随机深度图。在开放区间(0,1)的标准均匀分布中绘制合成深度图内像素的值

· 其次，我们生成随机大气光A (k, k, k)，其中k的值在0.85到1.0之间。

· 最后，我们根据式(1)和式(2)生成随机深度图d和随机大气光A的朦胧图像I。

5.3 学习策略

详细参数学习的公式推导感兴趣的读者可以自行查阅论文。作者使用了包含1.2亿个场景点的500个训练样本来训练我们的线性模型。训练了517个epoch，最后获得最佳学习结果为θ0 = 0.121779， θ1 = 0.959710， θ2 =−0.780245，σ = 0.041337。这些参数可以直接拿来使用，来恢复朦胧图像的景深。

5.4 深度信息估计

尽管在学习获得参数后，可以通过公式(8)来计算得到深度图，但是在某些特定情况，例如白色物体/过曝高光区域，这个估计可能失效，因为这一部分像素亮度高对比度，模型会认为这一部分区域是比较遥远的区域。

为了克服这个问题，我们需要考虑邻域中的每个像素。基于场景深度局部恒定的假设，我们通过以下方式处理原始深度图:

然而，同样明显的是，图像中出现了块状伪影。为了细化深度图，我们使用引导图像滤波[43]来平滑图像。图8(d)显示了模糊图像的最终恢复深度图。可以看到，阻塞工件被有效地抑制了。

6. 场景亮度恢复

6.1 大气光估计

由于恢复了输入模糊图像的景深图，就知道了景深的分布。地图上明亮的区域代表遥远的地方。根据式(6)，我们在深度图中选取前0.1%的最亮像素，在这些最亮像素中选取对应朦胧图像I中强度最高的像素作为大气光A

6.2 场景亮度恢复

请注意，散射系数β在均匀区域可视为常数[55]，它表示单位体积大气向各个方向散射光的能力。也就是说，β间接决定了除雾的强度。我们在图11中对此进行了说明。图11 (e-g)显示了不同β值下恢复的透射图，图11 (b-d)显示了相应的去雾结果。可以看到，一方面，小的β导致小的透射率，相应的结果在遥远的区域仍然是模糊的(见图11(b)和图11(e))。另一方面，过大的β可能导致对透射率的高估(见图11(d)和图11(g))。因此，在处理具有密集雾霾区域的图像时，需要适度的β。在大多数情况下，β = 1.0就足够了。

7. 实验

7.1 参数设置

7.2 定性比较

7.3 定量比较

7.3.1 耗时比较

7.4.2 MSE指标比较

7.4.3 SSIM指标比较

8. 结论

在本文中，我们提出了一种基于模糊图像中像素的亮度和饱和度差异的线性颜色衰减先验算法。利用这种简单但功能强大的先验建立模糊图像的场景深度线性模型，并使用监督学习方法学习模型参数，可以很好地恢复图像的深度信息。利用该方法得到的深度图，可以很容易地恢复朦胧图像的场景亮度。实验结果表明，该方法具有显著的除雾效率和良好的除雾效果。

虽然我们已经找到了一种用模糊图像的亮度和饱和度来模拟场景深度的方法，但仍然存在一个普遍的问题需要解决。即在非均匀大气条件下，大气散射模型中的散射系数β不能视为常数。例如，距离观测者几公里远的区域β值应该很低。因此，基于大气散射模型的消雾算法在某些情况下容易低估透射率。由于几乎所有现有的单幅图像去雾算法都是基于常数β假设，因此迫切需要一个更灵活的模型。为了克服这一挑战，可以考虑一些更先进的物理模型[63]。我们把这个问题留给以后的研究。