周报4_YMK
FlashAttention
硬件知识
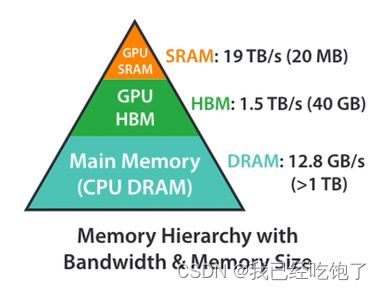
以 A100 (40GB HBM) 为例,下面显示其内存层次结构的粗略图。SRAM内存分布在108个流式多处理器(SMs)上,每个处理器192KB。片上SRAM比HBM快得多,但比HBM小得多,在计算方面,使用Tensor Core的BFLOAT16 的理论峰值吞吐量为 312 TFLOPS。GPU 的典型操作方式是使用大量的线程来执行一个操作,这个操作被称为内核。输入从HBM加载到寄存器和SRAM,并在计算后写回HBM。
算法对于内存带宽的需求通常使用 计算强度 (arithmetic intensity) 来表示,单位是 OPs/byte。意思是在算法中平均每读入单位数据,能支持多少次运算操作。它有助于理解操作的瓶颈,即计算约束(Compute-bound)或带宽约束(Bandwidth-bound, or Memory-bound)。
- 算力 π \pi π :也称为计算平台的性能上限,指的是一个计算平台倾尽全力每秒钟所能完成的浮点运算数。单位是
FLOPSorFLOP/s。 - 带宽 β \beta β :也即计算平台的带宽上限,指的是一个计算平台倾尽全力每秒所能完成的内存交换量。单位是
Byte/s。 - 计算强度上限 I m a x = π β I_{max}=\frac{\pi}{\beta} Imax=βπ :两个指标相除即可得到计算平台的计算强度上限。它描述的是在这个计算平台上,单位内存交换最多用来进行多少次计算。单位是
FLOPs/Byte。 - 模型的理论性能 P P P:我们最关心的指标,即模型在计算平台上*所能达到的每秒浮点运算次数(理论值)*。单位是
FLOPSorFLOP/s。
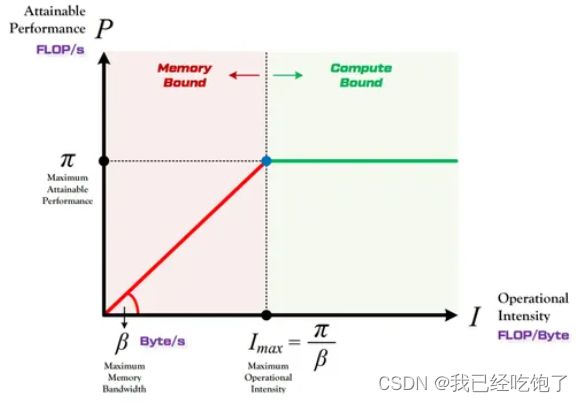
如下图所示,Roof-line 描述了模型在一个计算平台的限制下,到底能达到多快的浮点计算速度,即算力决定“屋顶”的高度(绿色线段),带宽决定“房檐”的斜率(红色线段)。
- 计算约束——此时HBM访问所花费的时间相对较低,不管模型的计算强度 I I I 有多大,它的理论性能 P P P 最大只能等于计算平台的算力 π \pi π。例如,具有较大内维数的矩阵乘法和具有大量通道的卷积。
- 带宽约束——当模型的计算强度 I I I 小于计算平台的计算强度上限 I m a x I_{max} Imax 时,由于此时模型位于“房檐”区间,因此模型理论性能 P P P 的大小完全由计算平台的带宽上限 β \beta β(房檐的斜率)以及模型自身的计算强度 I I I 所决定。例如,逐元素操作 (如activation, dropout 等) 和 规约操作 (如sum, softmax, batch normalization, layer normalization等)。
在 self-attention 中,计算速度比内存速度快得多,因此进程(操作)越来越多地受到内存(HBM)访问的瓶颈。因此,FlashAttention论文的目标是尽可能高效地使用SRAM来加快计算速度。
标准Attention
A t t r n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attrntion(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V Attrntion(Q,K,V)=softmax(dkQKT)V
其中 Q , K , V ∈ R n × d Q,K,V\in \Bbb{R}^{n\times d} Q,K,V∈Rn×d,$ N$ 表示序列长度, d d d 表示维度
一些中间变量 S = Q K T ∈ R N × N S=QK^T \in \Bbb{R}^{N\times N} S=QKT∈RN×N, P = s o f t m a x ( S ) ∈ R N × N P=softmax(S) \in \Bbb{R}^{N\times N} P=softmax(S)∈RN×N, O = P V ∈ R N × d O=PV \in \Bbb{R}^{N\times d} O=PV∈RN×d
标准的 self-attention 需要反复的对 HBM 进行读写
FlashAttention
在标准Attention中,一种方式是将Mask和SoftMax部分融合,以减少访存次数。然而,FlashAttention则更加激进,它将从输入 Q , K , V \mathbf{Q}, \mathbf{K}, \mathbf{V} Q,K,V到输出 O \mathbf{O} O的整个过程进行融合,以避免 S , P \mathbf{S}, \mathbf{P} S,P矩阵的存储开销,实现端到端的延迟缩减。然而,由于输入的长度 N N N通常很长,无法完全将完整的 Q , K , V , O \mathbf{Q}, \mathbf{K}, \mathbf{V},\mathbf{O} Q,K,V,O及中间计算结果存储在SRAM中。因此,需要依赖HBM进行访存操作,与原始计算延迟相比没有太大差异,甚至会变慢(没具体测)。
为了让计算过程的结果完全在SRAM中,摆脱对HBM的依赖,可以采用分片操作,每次进行部分计算,确保这些计算结果能在SRAM内进行交互,待得到对应的结果后再进行输出。
这个过程中,有一点需要注意的是,之前对于softmax的计算是以行为单位的,如下所示:
m ( x ) : = max i x i , f ( x ) : = [ e x 1 − m ( x ) … e x B − m ( x ) ] , ℓ ( x ) : = ∑ i f ( x ) i , softmax ( x ) : = f ( x ) ℓ ( x ) \begin{equation} m(x):=\max _i x_i, \quad f(x):=\left[\begin{array}{lll} e^{x_1-m(x)} & \ldots & e^{x_B-m(x)} \end{array}\right], \quad \ell(x):=\sum_i f(x)_i, \quad \operatorname{softmax}(x):=\frac{f(x)}{\ell(x)} \end{equation} m(x):=imaxxi,f(x):=[ex1−m(x)…exB−m(x)],ℓ(x):=i∑f(x)i,softmax(x):=ℓ(x)f(x)
当我们将输入进行分片后,无法对完整的行数据执行Softmax操作。这是因为Softmax函数在计算时需要考虑整个行的数据。然而,我们可以通过如下所示增量的方法来获得与完整行Softmax相同的结果,而无需使用近似操作。
m ( x ) = m ( [ x ( 1 ) x ( 2 ) ] ) = max ( m ( x ( 1 ) ) , m ( x ( 2 ) ) ) , f ( x ) = [ e m ( x ( 1 ) ) − m ( x ) f ( x ( 1 ) ) e m ( x ( 2 ) ) − m ( x ) f ( x ( 2 ) ) ] , ℓ ( x ) = ℓ ( [ x ( 1 ) x ( 2 ) ] ) = e m ( x ( 1 ) ) − m ( x ) ℓ ( x ( 1 ) ) + e m ( x ( 2 ) ) − m ( x ) ℓ ( x ( 2 ) ) , softmax ( x ) = f ( x ) ℓ ( x ) . \begin{equation} \begin{aligned} & m(x)=m\left(\left[x^{(1)} x^{(2)}\right]\right)=\max \left(m\left(x^{(1)}\right), m\left(x^{(2)}\right)\right), \quad f(x)=\left[\begin{array}{ll} e^{m\left(x^{(1)}\right)-m(x)} f\left(x^{(1)}\right) & e^{m\left(x^{(2)}\right)-m(x)} f\left(x^{(2)}\right) \end{array}\right], \\ & \ell(x)=\ell\left(\left[x^{(1)} x^{(2)}\right]\right)=e^{m\left(x^{(1)}\right)-m(x)} \ell\left(x^{(1)}\right)+e^{m\left(x^{(2)}\right)-m(x)} \ell\left(x^{(2)}\right), \quad \operatorname{softmax}(x)=\frac{f(x)}{\ell(x)} . \end{aligned} \end{equation} m(x)=m([x(1)x(2)])=max(m(x(1)),m(x(2))),f(x)=[em(x(1))−m(x)f(x(1))em(x(2))−m(x)f(x(2))],ℓ(x)=ℓ([x(1)x(2)])=em(x(1))−m(x)ℓ(x(1))+em(x(2))−m(x)ℓ(x(2)),softmax(x)=ℓ(x)f(x).
FlashDecoding
然而,上述优化不适合直接应用于推理过程。因为在训练过程中,FlashAttention对batch size和query length进行了并行化加速。而在推理过程中,batchsize通常为1, 导致FlashAttention对GPU利用率非常低
且FlashAttention是按顺序更新output的,因为 O ( 2 ) O^{(2)} O(2)的计算过程依赖 O ( 1 ) O^{(1)} O(1),有一个获取上一个块的最大值的过程。
Flash-Decoding在此基础上增加了一个新的并行化维度:keys/values的序列长度。即使batch size很小,但只要上下文足够长,它就可以充分利用GPU。与FlashAttention类似,Flash-Decoding几乎不用额外存储大量数据到全局内存中,从而减少了内存开销。
这一切之所以可行,都是因为注意力 softmax 可以进行迭代计算。在 Flash-Decoding 中,它在两个级别上被使用:在分块内部(类似 FlashAttention),以及跨分块进行最终的归约计算。
代码方面
还在跑和看Medusa头的代码