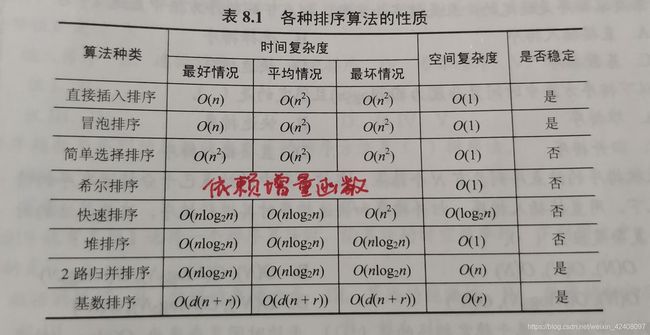
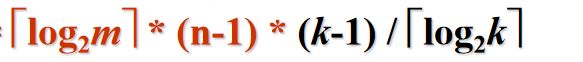排序算法总结

选择排序：与序列初始状态无关

• 从最左端或最右端开始有序

简单选择排序

• 总共需要进行n躺操作（1<=i<=n）,每趟操作选出待排序的部分[i,n]中最小的元素，令其与A[i]交换。

• 从后面找出最小的，和前面的换

• 时间复杂度为O（n²）

• 空间复杂度 O(1)

• 不稳定

void selectSort()
{
	for(int i=i;i<=n;i++){
		int k=i;
		for(int j=i;j<=n;j++){
			if(A[j]<A[k]){
				k=j;
			}
		}
		int temp = A[i];
		A[i] = A[k];
		A[k]=temp; 
	}
}

锦标赛排序

两两比较 找出winner

胜者树：

• 如果中间一个选手值改变了，沿着叶子结点走到根 来改 ，不影响别的比赛
• 重构：比较父结点与兄弟结点

堆排序

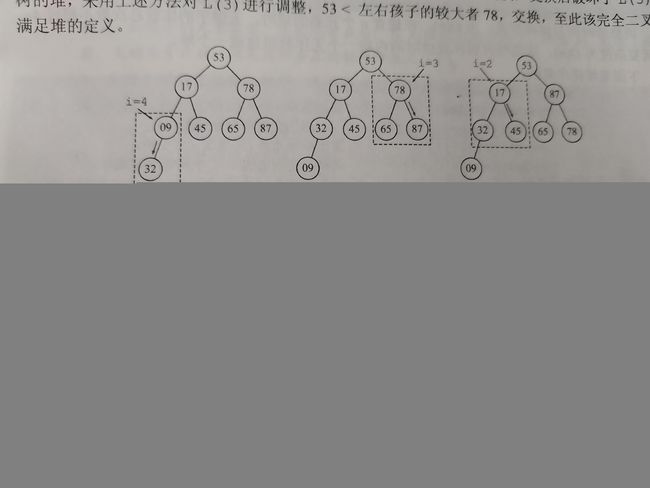
• 堆排序的思想借助于二叉堆中的最大堆得以实现。首先，将待排序数列抽象为二叉树，并构造出最大堆；然后，依次将最大元素（即根节点元素）与待排序数列的最后一个元素交换（即二叉树最深层最右边的叶子结点元素）；
• 每次遍历，刷新最后一个元素的位置（自减1），直至其与首元素相交，即完成排序。
• 大根堆：最大元素存放在根节点；任一非根结点的值小于等于其双亲的结点值。
• 输出堆顶元素后，将堆的最后一个元素与堆顶元素交换
• 适合关键字较多的情况，可以选出前n的最大值
• n个关键字的小根堆中，关键字最大的记录（在叶子结点中）有可能存储在(n/2)+2的位置
• 向n个结点的堆中插入或删除一个新元素，时间复杂度 O(log2n) ； 树的高度 log2n+1
• 构建一个新堆，时间复杂度 O(n)
• 最好、最坏、平均 时间复杂度：O(nlog2n) 　　稳定性：不稳定
  

  void heapSort(int[] nums) {
        int size = nums.length;
        for (int i = size/2-1; i >=0; i--) {
            adjust(nums, size, i);
        }
        for (int i = size - 1; i >= 1; i--) {
            int temp = nums[0];
            nums[0] = nums[i];
            nums[i] = temp;
            adjust(nums, i, 0);
        }
    }
    void adjust(int []nums, int len, int index) {
        int l = 2 * index + 1;
        int r = 2 * index + 2;
        int maxIndex = index;
        if (l<len&&nums[l]>nums[maxIndex])maxIndex = l;
        if (r<len&&nums[r]>nums[maxIndex])maxIndex = r;
        if (maxIndex != index) {
            int temp = nums[maxIndex];
            nums[maxIndex] = nums[index];
            nums[index] = temp;
            adjust(nums, len, maxIndex);
        }
    }

插入排序

• 从前面开始有序

直接插入排序

• 有序序列 ----- 无序序列
• 最多比较次数：n(n-1)/2 逆序列
• 最少比较次数：n-1 排好的
• 空间效率 ： O(1)
• 时间效率：取决于待排序表的初始状态
• 时间复杂度：O(n²) 　　稳定性：稳定
• 适用于顺序存储和链式存储的线性表
• 可能出现：在最后一趟之前，所有元素都不在最终位置上

void InsertSort( ElemType A[],int n)
{
   int i,j;
   for(int i=2;i<n;i++) //依次将2~n 的插入
   	if(A[i] < A[j-1]){ //小于，往前放
   		A[0] = A[i]; //复制为哨兵，A[0]不存放位置
   		for(int j=i-1;A[0]<A[j];j--) // 从后往前在有序列表找代插入位置
   			A[j+1]=A[j];  // 向后挪位
   		A[j+1]=A[0]; //复制到插入位置
   	}
}

折半插入排序

• 只是在查找时采用折半查找
• 仅减少了比较次数，为O( n log 2 n )；比较次数与待排序表的初始状态无关，仅取决于表中的元素个数n
• 时间复杂度：O(n²) 　　稳定性：稳定

void InsertSort( ElemType A[],int n)
{
   int i,j,low,high,mid;
   for(int i=2;i<n;i++) //依次将2~n 的插入
   	A[0] = A[i];
   	low = 1;high = i-1;
   	while(low <=high){
   		mid=(low+high)/2;
   		if(A[mid]>A[0}) high = mid-1;
   		else low = mid+1;
   	}
   	for(int j=i-1;j>=high+1;--j) // 从后往前在有序列表找代插入位置
   		A[j+1]=A[j];  // 向后挪位
   	A[high+1]=A[0]; //复制到插入位置
   	}
}

希尔排序 (缩小增量排序)

• 插入排序的改进版。为了减少数据的移动次数，在初始序列较大时

• 取较大的步长，通常取序列长度的一半，此时只有两个元素比较，交换一次；

• 之后步长依次减半直至步长为1，即为插入排序，由于此时序列已接近有序，故插入元素时数据移动的次数会相对较少，效率得到了提高。

• 空间复杂度O(1)

• 时间复杂度：通常认为是O(n^1.5) 　　稳定性：不稳定

• 最坏情况下，时间复杂度 O(n²)

• 仅适用于线性表为顺序存储的情况

    void ShellSort(ElemType A[],int n){
    	for(dk=n/2;dk>=1;dk=dk/2) //步长变化
    		for(i=dk+1;i<=n;++i)  
    			if(A[i]<A[i-dk]){ 
    				A[0]=A[i];  //暂存在A[0]
    				for(j=i-dk;j>0&&A[0]<A[j];j-=dk) //记录后移查找插入位置
    					A[j+dk]=A[j];
    				A[j+dk]=A[0];
    			}
    }   

归并排序

• 采用了分治和递归的思想，递归&分治-排序整个数列如同排序两个有序数列，依次执行这个过程直至排序末端的两个元素，再依次向上层输送排序好的两个子列进行排序直至整个数列有序（类比二叉树的思想，from down to up）。
• 时间复杂度：O(nlog2n) 　　稳定性：稳定
• 对与n个元素进行k路归并排序时，趟数m满足k^m=n

[L1,R1]  [L2,R2]
i           j

merge(int A[],int L1,int R1,int L2,int R2){
	int i=L1,j=L2;
	int temp[maxn],index = 0;
	while(i<=R1&&j<=R2){
		if(A[i]<A[j]){
			temp[index++]=A[i++];
		}else{
			temp[index++]=A[j++]; 
		}
	}
	while(i<=R1) temp[index++]=A[i++]; //将[L1,R1]中剩余的元素加入temp 
	while(j<=R2) temp[index++]=A[j++]; //将[L2,R2]中剩余的元素加入temp
	for(int i=0;i<index;i++){  //将temp赋值回原数组 
		A[L1+i] = temp[i];
	}
}

void mergeSort(int A[],int left,int right){
	if(left<right){
		int mid = left+(right-left)/2;
		mergeSort(A,left,mid);
		mergeSort(A,mid+1,right);
		merge(A,left,mid,mid+1,right);
	}
} 

练习题 数组中的逆序对

2-路归并排序

• 将序列两两分组，将序列归并为n/2 个组，组内单独排序；然后将这些组再两两归并，生成n/4 个组，组内再单独排序；以此类推，直到只剩下一组为止。
• 空间复杂度 O(n)
• 每趟复杂度O(n)，共 log2n趟，时间复杂度为O（nlogn）。
• 稳定

交换排序

冒泡排序

• 空间复杂度为O(1)
• 最好情况下时间复杂度 O(n)
• 最坏情况下、平均 时间复杂度O(n^2)
• 稳定
• 每趟排序都会有一个元素被放置在最终位置上
• 从最左端或最右端开始有序

  void BubbleSort(vector<int>& nums,int n){
        for(int i=0;i<n-1;i++) {
            bool flag = false;
            for(int j=n-1;j>i;j--) {
                if(nums[j-1]>nums[j]){
                    swap(nums[j-1],nums[j]);
                    flag = true;
                }
            }
            if(flag == false){
                return ;
            }
        }
    }

快速排序

• 基于分治法

1. 待排序表，左右设置两个指针
2. 以第一个元素为轴，pivot
3. 右边指针（j）开始找第一个小于pivot的元素，交换给左边指针（i）
4. 左边指针（i）开始找第一个大于pivot的元素，交换给右边指针（j）
5. 直至 i == j
6. 带排序表 被 pivot 元素分成两个待排序列
7. 分别再进行快速排序，直至，待排序列中只剩一个元素

• 性能主要取决于划分操作的好坏
• 空间效率：最好、平均 O（log2n） ； 最坏O（n）
• 时间效率：最坏 O（n²） 平均、最好O（nlog2n）
• 最坏情况：序列基本有序
• 快排是所有内部排序算法中平均性能最优的排序算法
• 不稳定
• 过程中，不产生有序子序列，但每趟排序会将 基准 元素放到最终位置上

基数排序

• 不基于比较和移动进行排序，而基于关键字各位的大小进行排序。
• 关键字有几位数，就排几趟
• 空间复杂度： r 个队列 O( r)
• 时间复杂度:一趟分配需要 O(n) 一趟收集需要 O ( r) ; d 趟总的需要 O(d (n+r) )
• 稳定

比较次数

1.2.3 6T

4.5.4 13T

8.1.2 4T

8.5.3 8T

内部排序

内部排序算法比较

时空复杂度

1. 时间复杂度
2. 空间复杂度

稳定性

过程特征

• 排序趟数与序列原始状态无关的是：直接插入排序（每趟插入一个新的，共n-1）、简单选择排序（每趟找到一个最小的/最大的，共n-1趟）、基数排序（与关键字位数有关）
• 每趟排序结束至少有一个元素在最终位置上：简单选择排序、快速排序、堆排序

排序算法选择

1. n较小：直接插入、简单选择
2. 初始状态基本有序：直接插入、冒泡排序；不要快速排序
3. n较大：快速排序、堆排序、归并排序；或先直接插入再两两归并
4. 当文件的n个关键字随机分布时，任何借助于“比较”的排序算法，至少需要O（nlog2n）的时间。
5. 记录本身信息量大，为避免移动，可采用链表作为存储结构。

一般情况下，查找效率最低的数据结构：堆

将顺序存储换为链式存储，希尔排序、堆排序 时间效率会降低

外部排序

• 为减少平衡归并中外存读写所采取的方法：增大归并路数（减少归并趟数）、减少归并段个数
• 时间代价主要考虑访问磁盘的次数，即I/O次数
• 通常采用归并排序法
  

（1）根据内存缓存区大小，将外存上的文件分为若干长度为l的子文件
（2）依次读入内存并利用内部排序方法对它们进行排序
（3）将排序好的有序子文件重新写回外存，称这些 有序子文件为 归并段 或 顺串

（4）对这些归并段进行逐趟归并，使归并段（有序子文件）逐渐由小到大
（5）直至得到整个有序文件为止

• 外部排序的总时间=内部排序时间+外存信息读写的时间（最大；以“磁盘块”为单位）+内部归并所需时间
  

• r个初始归并段（总记录/内存工作区可容纳的记录数），做k路平衡归并，树的高度 logkr = 归并趟数

• 传统总的比较次数：[log2r] (n-1)(k-1)/[log2k]

• 在做m路平衡归并排序的过程中，为实现输入\内部归并\输出的并行处理，需要设置2m个输入缓存区和2个输出缓、存区

败者树

• 采用败者树后总的比较次数：(n-1)[log2r] 与k无关

• 原来总的比较次数：

• 中间结点记录败者 胜者向上传

• 根节点记录的是败者，所以需要再拿一个结点来记录胜利者

• 重构：只需要和父结点比较
  -

置换-选择排序的作用是：用于生成外部排序的初始归并段

最佳归并树在外部排序中的作用：设计m路归并排序的优化方案

若初始归并段不足以构成一棵严格k叉树时，需添加长度为0的“虚段”

• 叶子结点 n ； k路归并
• （n-1）%(k-1) = u 就是有u个多余点
• 虚段数：k-u-1