数据结构和算法-哈夫曼树以相关代码实现

总览

带权路径长度

哈夫曼树的定义

一个含n个带权叶节点的二叉树对应形式有多种（左右也不是两种的形式），可自己去画画

哈夫曼树的构造

即权值最小的叶子节点作为最长路径的叶子节点

法1

法2

二者本质相同，都是每次从节点中找最小的两个合并为一个新节点

哈夫曼编码

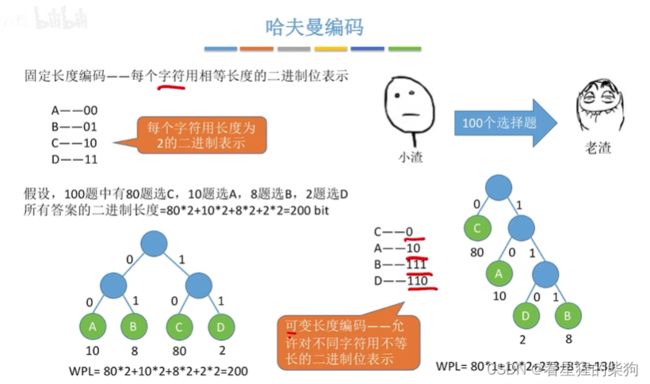
前缀编码就是不存在部分编码为其他编码的开头某部分
或者说不存在编码为其他编码的子集

英文字母频次

即各频率为权重，然后去构造对应的哈夫曼树，最后得出各自的编码
数据压缩率可以认为是 对应哈夫曼树的WPL / 用原来的固定长度编码对应的WPL

总结

实验内容： 哈夫曼树

一、上机实验的问题和要求（需求分析）：

[ 题目 ] （1）哈夫曼树问题。（2）利用哈夫曼编码进行通讯可以大大提高信道利用率，缩
短信息传输时间，降低传输成本，但是，这要求在发送端通过一个编码系统对待传数据进行
预先编码；在接受端将传来的数据进行解码（复原）对于双工信道（即可以双向传输的信道），
每端都要有一个完整的编/译码系统。试为这样的信息收发站写一个哈夫曼的编译码系统。

二、程序设计的基本思想，原理和算法描述：

1.实现哈夫曼编码首先需要构建最优二叉树，权值越大的叶节点越靠近根节点，其算法为：键盘输入的字符串长度决定最优二叉树的节点数，遍历这个字符串长度，创建具有字符长度n的单节点树。选取根节点权值最小和次小的两个根节点合成一棵树，重复这个过程——把根节点最小和次小的结合直到每个节点都出现在最优二叉树上。

2．构造哈夫曼编码：

左分支为0，右分支为1，各结点所对应的二进制编码为该节点的哈夫曼编码。采用叶节点向上回溯的方法，每退回一个就记录一位数字。将所得编码存入code[]。

3.编码：

根据所得哈夫曼树对比字符串，根据左分支为0右分支为1输出其对应编码。

4.解码：根据哈夫曼树回溯编码。

三、调试和运行程序过程中产生的问题及采取的措施：

使用printf打印相关内容，从而观察变化

四、源程序及注释

#include"stdio.h"
#include"stdlib.h"
#include"string.h"
#define status int
#define OK 1
#define Maxvalue 100
#define Maxleaf 30 
typedef struct
{ 
    int weight;
    int parent ,lchild,rchild ;
}HTNode,*HuffmanTree;

typedef char * *HuffmanCode; //指向字符指针的指针

status Select(HuffmanTree HT,int n,int &s1, int &s2) //选择最小的两个节点
{
    HuffmanTree p;int i;
    int lnode= Maxvalue,mnode= Maxvalue;
    for(p=HT,i=1;i<=n;i++)
    { 
        //lnode小于始终会小于mmnode，因为if的匹配顺序
        if(p[i].weight<lnode&&p[i].parent==0)// 判断该节点的权重是否小于当前的lnode并且已经有父节点的不要
    { 
        mnode=lnode;         //此时mmode更新为lnode
        lnode=p[i].weight;  //lnode更新为当前节点的权重
        s2=s1;          //S2为mmnode对应节点的索引 S1为lnode对应节点的索引 此时将mnode的索引更新
        s1=i;      //更新lnode的索引更新
    }
    else if(p[i].weight<mnode&&p[i].parent==0) //当该节点的权重大于lnode时并判断是否小于当前的mnode并且已经有父节点的不要
    {
        mnode=p[i].weight;   //更新mnode的为当前节点的权重
        s2=i;           //更新mnode此时的索引
    }
    }
    return OK;
}
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC, int *w,int n)
{   
    int i,m,start,f,s1=0,s2=0 ,c;char *cd;
    HuffmanTree p;
    if(n<=1)return;//叶子节点判断
    m=2*n-1;  //求出叶子节点对应的二叉树的节点个数 合并次数+节点个数=对应二叉树的节点个数
    HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
    for(p=HT+1,i=1;i<=n;++i,++p,++w)
    { 
        (*p).weight=*w;// 刚开始的节点赋权值
        (*p).parent=0; 
        (*p).lchild=0;
        (*p).rchild=0;
    }
    for(i=1;i<=n;i++)
    { 
        printf("刚开始的第%d个叶子节点weight：%d ,parent：%d ,lchild：%d ,rchild：%d ",i,HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild);
        printf("\n");  //刚开始的
    }
    for(;i<=m;i++)  
    { 
        (*p).weight=0; //其他节点初始化为0
        (*p).parent=0;
        (*p).lchild=0;
        (*p).rchild=0;
        p++; 
    }
    for(i=1;i<=m;i++)
    {   
        printf("初始化完成的哈夫曼树的第%d节点:%d ,%d ,%d ,%d ",i,HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild);
        printf("\n");}
    for(i=n+1;i<=m;++i)
    {
        Select(HT,i-1,s1,s2);  //传入的是原来的和新建的节点范围，返回的是对应节点中权重最小的两个
        HT[s1].parent=i;      //然后建立父子关系
        HT[s2].parent=i;
        HT[i].lchild=s1;
        HT[i].rchild=s2;
        HT[i].weight=HT[s1].weight+HT[s2].weight; //父节点的权重等于两个孩子的权重和
    }
    for(p=HT+1,i=1;i<=m;i++,p++)
    {
        printf("编码完成后的哈夫曼树的第%d个节点：%d,%d,%d,%d",i,(*p).weight,(*p).parent,(*p).lchild,(*p).rchild); 
        printf("\n");
    } 
    //从叶子到根逆向求每个字符的赫夫曼编码
        HC=(HuffmanCode )malloc((n+1) *sizeof(char *)); //编码的字符串地址数组 大小为(n+1)*8 但类型为HuffmanCode，即单位为八个字节 指向char* 
        cd=(char*)malloc(n*sizeof(char));// n个字符的指针，对应编码结果
        cd[n-1]='\0'; //结束符
        for(i=1;i<=n;++i) //遍历初始的叶子的节点
        {
        start=n-1;    //编码从后往前一个一个字符的赋值
        for(c=i,f=HT[i].parent; f!=0; c=f,f=HT[f].parent) //从初始叶子节点遍历父节点，直到对应父节点为0时停止
        {
        if(HT[f].lchild==c) cd[--start]='0'; //如果父节点的左孩子为当前节点则此时编码为0
        
        else cd[--start]='1'; //如果父节点的右孩子为当前节点则此时编码为1

        }//则当前叶子节点对应的编码转换完成
        HC[i]=(char *)malloc((n-start)*sizeof(char));//赋予满足编码长度的字符串地址
        strcpy(HC[i],&cd[start]); //赋值给当前节点的编码
        printf("当前第%d个叶子的编码为：%s\n",i,HC[i]); 
        }
        free(cd);
}

int main()
{
    HuffmanTree HT;HuffmanCode HC;
    int n,i; int w[8]={5,29,7,8,14,23,3,11};
    printf("%d",sizeof(char *));
    printf("请输入叶子节点的个数：\n");
    scanf("%d",&n); //输入叶子节点的个数
    HuffmanCoding(HT,HC, w,n); //生成哈夫曼树并输出对应各个叶子节点的编码
    return 0;
}

五、运行结果