1. K-Means算法介绍
K-Means作为聚类算法中的典型代表,比较容易实现。
聚类算法又叫做“无监督分类”,其目的是将数据划分成有意义或有用的组(或簇)。这种划分可以基于业务需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中,如果手头有大量的当前和潜在客户的信息,可以使用聚类将客户划分为若干组,以便进一步分析和开展营销活动。再比如,聚类可以用于降维和矢量量化,可以将高维特征压缩到一列当中,常常用于图像、声音和视频等非结构化数据,可以大幅度压缩数据量。
K-Means的工作原理:
K-Means算法是将一组N个样本的特征矩阵划分为K个无交集的簇;直观上是一组一组聚类
在一起的数据,在一个簇中的数据就是同一类。簇就是聚类的结果表现。
簇中所有数据的均值即:“簇的质心”。
在K-Means算法中,簇的个数K是一个超参数,需要人为输入来确定。K-Means的核心任务就是根据设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:
1.首先随机选取样本中的K个点作为聚类中心;
2.分别算出样本中其他样本距离这K个聚类中心的距离,并把这些样本分别作为自己最近的那个聚类中心的类别;
3.对上述分类完的样本再进行每个类别求平均值,求解出新的聚类质心;
4.与前一次计算得到的K个聚类质心比较,如果聚类质心发生变化,转过程b,否则转过程e;
5.当质心不发生变化时(当我们找到一个质心,在每次迭代中被分配到这个质心上的样本都是一致的,即每次新生成的簇都是一致的,所有的样本点都不会再从一个簇转移到另一个簇,质心就不会变化了),停止并输出聚类结果。
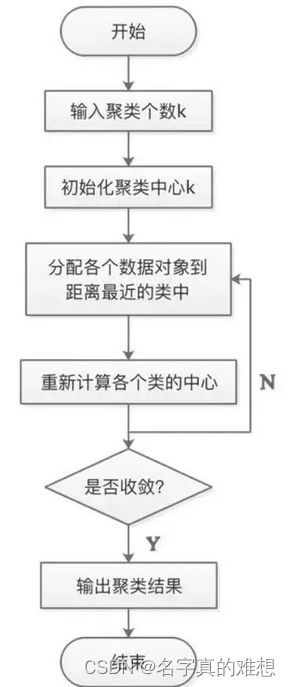
流程图如下:
簇内误差平方和的定义:
聚类算法聚出的类有什么含义呢?这些类有什么样的性质?
我们认为,被分在同一个簇中的数据是有相似性的,而不同簇中的数据是不同的,当聚类完毕之后,接下来需要分别研究每个簇中的样本都有什么样的性质,从而根据业务需求制定不同的商业或者科技策略。聚类算法追求“簇内差异小,簇外差异大”。而这个 “差异”便是通过样本点到其簇质心的距离来衡量。
对于一个簇来说,所有样本点到质心的距离之和越小,便认为这个簇中的样本越相似,簇内差异越小。而距离的衡量方法有多种,令x表示簇中的一个样本点,μ表示该簇中的质心,n表示每个样本点中的特征数目,i表示组成点x的每个特征,则该样本点到质心的距离可以由以下距离来度量:

采用欧几里德距离,那么同一个簇中样本点到质心的距离平方和为:

其中,m为一个簇中样本的个数,j是每个样本的编号。这个公式被称为簇内平方和(Cluster Sum of Square),又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加,就得到了整体平方和(Total Cluster Sum of Square),又叫做Total Inertia。
Total Inertia越小,代表着每个簇内样本越相似,聚类的效果就越好。因此K-Means追求的是:求解能够让Inertia最小化的质心。实际上,在质心不断变化不断迭代的过程中,总体平方和是越来越小的。我们可以通过数学来证明,当整体平方和达到最小值的时候,质心就不再发生变化了。如此,K-Means的求解过程,就变成了一个最优化问题。
在K-Means中,在一个固定的簇数K条件下,最小化总体平方和来求解最佳质心,并基于质心的存在去进行聚类。两个过程十分相似,并且整体距离平方和的最小值其实可以使用梯度下降来求解。
Inertia是基于欧几里得距离的计算公式得来的。实际上,也可以使用其他距离,每个距离都有自己对应的Inertia。在过去的经验中,已经总结出不同距离所对应的质心选择方法和Inertia,
在K-Means中,只要使用了正确的质心和距离组合,无论使用什么距离,都可以达到不错的聚类效果。
因此,K-Means可以被用在很多数据最优化的问题当中。
参考了文章:
百度安全验证
2. K-Means_C++实现
K_Means的C++代码如下:
#include
#include
#include
然后我是在Linux系统下,使用的CMake工程进行编译的。
编译完成后,使用:
./生成的可执行文件名 数据集 将数据划分为几类
在我的电脑上,是这样执行的:
./K_Means ../1.txt 3
然后将会生成一个结果文件,具体如下:

将会对数据进行分类。可视化可以使用python进行处理,在这里不演示。
数据集比较小:
(2.3, 4.9), (6.9, 7), (7, 2.6), (1.1, 0.8), (4.4, 5.5), (3.2, 2.3), (2.8, 5.8), (5, 4.8), (9.2, 9.1), (8.4, 0.7)
参考文章如下:
【机器学习实战之三】:C++实现K-均值(K-Means)聚类算法_c++聚类-CSDN博客



