数据结构学习第八章排序

第八章排序

8.1基本概念

• 排序：将一组杂乱无章的数据按照一定规律顺次排列起来。也就是把无序序列排成一个有序序列(由大到小 或者 由小到大)的运算。

• 排序分类：

①按照存储介质可分为：

*内部排序：数据量不大，数据在内存中排序，无序内外存交换数据。

*外部排序：数据量较大，要将数据分批调入内存来排序，中间结果还要及时放入外存，显然外部排序要复杂得多。

②按照比较器个数可分为：

*串行排序：单处理机

*并行排序：多处理机

③按照主要操作可分为：

*比较排序：插入排序、交换排序、选择排序、归并排序

*基数排序：不比较元素的大小，仅根据元素本身的取值确定其有序位置

④按照辅助空间分为：

*原地排序：辅助空间用量为O(1)的排序，即所占的辅助存储空间与参加排序的数据量大小无关。

*非原地排序：辅助空间用量超过O(1)的排序

⑤按照稳定性可分为：

*稳定排序：能够使任何数值相等的元素，排序以后相对次序不辩

*非稳定排序：不是稳定排序的方法

⑥按照自然性可分为：

*自然排序：输入的数据越有序，排序的速度越快的排序方法

*非自然排序：不是自然排序的方法

• 按排序依据原则：

—插入排序：直接插入排序、折半插入排序、希尔排序

—交换排序：冒泡排序、快速排序

—选择排序：简单选择排序、堆排序

—归并排序：2-路归并排序

—基数排序

• 这里学习的排序，记录序列以顺序表存储。

#define MAXSIZE 20  //定义记录最大个数
typedef int KeyType;  //设置关键字类型

typedef struct {
    KeyType key;  //关键字
    InfoType otherinfo; //其他数据项
}RedType;  

typedef struct{
    RedType r[MAXSIZE + 1];  //定义顺序表的向量，一般来说r[0]作为哨兵或者缓冲区
    int length;
}SqList;

8.2插入排序

• 基本思想：每步将一个待排序的对象，按照其关键码大小，插入到前面已经排好序的一组对象的适当位置上，直到对象全部插入为止。也就是说，边插入边排序，保证子序列中随时都是排好序列的。
• 对于找到要插入的位置，有三个不同的方法：

*顺序定位插入位置——直接插入排序

*二分法定位插入位置——二分插入排序

*缩小增量多遍插入——希尔排序

8.2.1直接插入排序

【算法思想】

①以第一个元素开始，作为已经排序好的子序列。已经排序好子序列的后一位元素作为插入对象。

②子序列从后往前与插入对象比较：

如果子序列中元素大于插入对象，往后移一位。

如果子序列中元素小于插入对象，插入对象插入到这个元素的后一位。

③重复①②直到排序完整个序列为止。

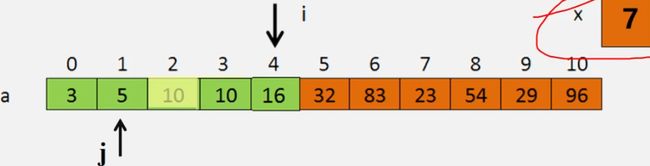
【例】绿色结点为已经排序好的元素，橙色结点为未排序的元素。

排序步骤：

①用一个变量x记录要插入的对象

16＞7，则a[3]往后移位，a[4]=a[3];

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-a7qr8Fxx-1691835501230)(F:/%E6%A1%8C%E9%9D%A2%E6%96%87%E4%BB%B6/%E7%BC%96%E7%A8%8B%E5%AD%A6%E4%B9%A0/img/image-20230807111857769-16918351588467.png)]

②10＞7，则a[2]往后移位，a[3]=a[2];

③5＜7，则把元素插入到a[1]的后一位。a[2]=x；

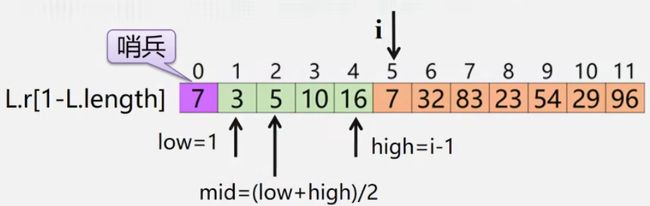
【例】有另一种排序方法，把数组a[0]置空作为哨兵，要排序的时候可以将要插入的对象存入到a[0]。

【算法实现】

//用哨兵的方法来实现直接插入排序
void InsertSort(SqList &L){
    int i,j;
    for(i=2;i<=L.length;i++){  //哨兵元素未记录到表长，且a[1]作为默认的已经排序好的子序列，从下标2开始
        if(L.r[i].key < L.r[i-1].key){  //要插入对象 ＜ 已经排序好子序列最后一位，开始操作
            L.r[0] = L.r[i]; //复制哨兵
            for(j=i-1;L.r[0].key < L.r[j].key;j--){  //将所有比要插入对象大的元素往后移一位
                L.r[j+1]=L.r[j];
            }
            L.r[j+1]=L.r[0]; //把插入对象插入到相应位置
        }
    }
}

【算法分析】

• 原始数据越接近有序，排序速度越快。

• 最坏情况下（输入数据是逆序），时间复杂度O(n²)。最好情况下（已经排序好），时间复杂度O(n)。

• 平均情况下，耗时是最坏情况下的一半，时间复杂度O(n²)。

• 这是一个稳定的排序方法。

8.2.2折半插入排序

折半插入排序与直接插入排序相比，只是在查找插入位置时，采用折半查找法。

【算法思想】

①以第一个元素开始，作为已经排序好的子序列。已经排序好子序列的后一位元素作为插入对象。

②将插入对象在已经排序好的子序列中进行折半查找，找到小于插入对象的值，把插入对象插入到其后一位。

③重复①②直到排序完整个序列为止。

【算法实现】

void BInsertSort(SqList &L){
    for(i=2;i<=L.length;i++){ //依次插入第2到第n个元素
        L.r[0] = L.r[i];
        low = 1;high = i-1; //折半查找两个标记
        while(low<=high){
            mid=(low + high) /2;
            if(L.r[0].key < L.r[mid].key) high = mid-1;
            else low = mid+1;
        } //循环结束时，high+1为要插入的位置。即r.[high].key
        for(j=i-1;j>=high+1;--j){
            L.r[j+1]=L.r[j];
        }
        L.r[high+1]=L.r[0];
    }
}

【算法分析】

• 时间复杂度O(n²)。空间复杂度O(1)。

• 这是一个稳定的排序算法。

• 折半查找比顺序查找快，所以折半插入排序的平均性能比直接排序较快。

• 若对象的初始排列已经按照关键码排好序或接近有序时，直接插入排序比折半插入排序执行关键码比较次数少。

• 折半插入排序的对象移动次数与直接排序相同。折半查找只减少了比较次数没有减少移动次数。

8.2.3希尔排序

• 希尔插入排序与直接插入排序相比，只是在移动元素上进行调整。

• 希儿排序特点：缩小增量，多遍插入排序

【算法思想】

①选取一个增量序列，这个序列是逐次递减的。如D3=5，D2 = 3，D1=1。

①对每个Dk进行间隔分割，分别进行直接插入排序。如这里首先是D3，每个间隔为5。

②待整个序列中的记录基本有序时，再整体进行一次直接插入排序。

③重复①②，直到间隔为1排序完成。

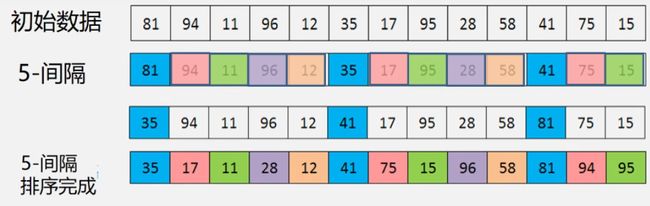
【例】

①选取间隔为5作为一组进行间隔之间的直接排序排序。

②选取间隔为3作为一组进行间隔之间的直接排序排序。

③最后间隔1进行间隔之间的直接排序排序。

【特点】

• 一次移动的位置较大，跳跃式地接近排序后的最终位置。
• 最后一次仅需要少量移动，增量序列必须是递减且互质的，最后一个必须是1。

【算法实现】

void ShellSort(SqList &L,int dlta[],int t){//dalt[]中存放增量序列，t表示使用dalt中0~t-1元素作为增量序列
    //按照增量序列对顺序表L作希尔排序
    for(k=0;k<t;k++){
        ShellInsert(L,dlta[k]); //一趟增量为dlta[k]的插入排序
    }
}

//某一趟的排序操作
void ShellInsert(SqList &L,int dk){
    for(i=dk+1;i<=L.length;++i){   
        if(r.[i].key <r.[i-dk].key){
            r[0]=r[i];
            for(j=i-dk;j>0 && (r[o].key < r.[j].key);j=j-dk)
                r[j+dk]=r[j];
            r[j+dk]=r[0];
        }
    }
}

【算法分析】

• 希尔排序是一种不稳定算法
• 希尔排序的算法效率与增量序列取值有关

8.3交换排序

• 基本思想：两两比较，如果发生逆序，则交换，直到所有记录都排序好为止。

• 常见的交换排序：冒泡排序—O(n²)；快速排序—O(n log2 n)

8.3.1冒泡排序

【算法思想】

①可以从前往后（也可以从后往前），依次两两比较，不符合规则的即交换。

②经过一趟比较后，已经有一个处于正确的位置，减去这个元素继续冒泡排序。

③有n个元素，经过n-1趟排序后，排序完成。

【算法思想】

void bubble_sort(SqList &L){
    int m,i,j;
    RedType x;  //用于交换的临时存储空间
    for(m=1;m<=n-1;m++){  //总共需要n-1趟
        for(j=1;j<n-m;j++){  //每趟两两比较，需要比较m-1次。
            if(L.r[j].key>L.r[j+1].key){ //这里是从小到大排序，所以如果前一个元素 ＞ 后一个元素，需要操作
                //交换
                x=L.r[j];
                L.r[j]=L.r[j+1];
                L.r[j+1]=x;
            }//end if
        }//end forj
    }//end form
}

【特点】

优点：每趟结束时，总有一个元素到相应位置。

提高效率：当某一趟未出现交换记录，则已经排好序可以结束了。

【改进冒泡排序】

void bubble_sort(SqList &L){
    int m,i,j;
    RedType x;  //用于交换的临时存储空间
    int flag =1;  //用于标记有交换记录，刚开始需要启动循环，置为1
    for(m=1;m<n-1 && flag ==1;m++){//总共需要n-1趟排序。且需要flag有记录到有交换记录
        flag=0;//刚进来循环，还未有交换记录，先置0。
        for(j=1;j<m-1;j++){
            if(L.r[j].key > L.r[j+1].key){ //这里从小到大排序，所以如果前一个元素 ＞ 后一个元素，需要操作
                flag=1; //有交换记录，记录
                //交换
                x=L.r[j];
                L.r[j]=L.r[j+1];
                L.[j+1]=x;
            }
        }
        
    }
}

【算法分析】

• 冒泡排序最好、最坏、平均时间复杂度O(n²)。
• 需要一个交换的辅助空间，空间复杂度O(1)。
• 冒泡排序是一个稳定的算法。

8.3.2快速排序

【算法思想】

①任取一个元素为中心

②所有比它小的元素一律前放，比它大的元素一律后放。形成左右两个子表。

③在这两个子表中重复①②直到每个子表中只剩下一个元素。

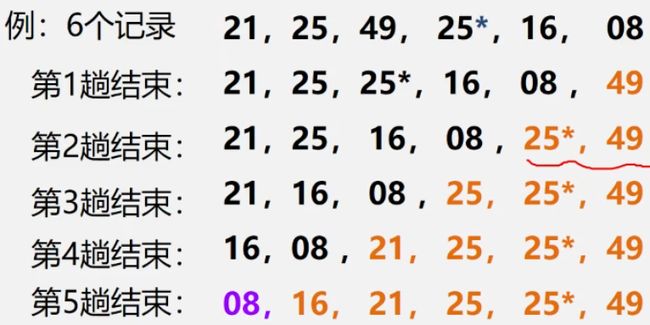
【例】

（49 ，38， 65 ，97 ，76 ，13，27，49），选第一个49进行一趟快速排序。

①取49到哨兵结点

②我们默认相等的也放到右边，即 元素 ≥ 中心结点，放到右边

③27比49小，放到左边

④38比49小，下标往后移一位，65比49大，放到右边

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BIrcgfZM-1691835501233)(F:/%E6%A1%8C%E9%9D%A2%E6%96%87%E4%BB%B6/%E7%BC%96%E7%A8%8B%E5%AD%A6%E4%B9%A0/img/image-20230807164351149-169183526205940.png)]

⑤以此类推，当low >=high时，找到中心结点。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wPmM8aXl-1691835501233)(F:/%E6%A1%8C%E9%9D%A2%E6%96%87%E4%BB%B6/%E7%BC%96%E7%A8%8B%E5%AD%A6%E4%B9%A0/img/image-20230807164414311-169183527261843.png)]

⑥把49放入中心结点，分成左右两个表。左右两个表再按照此方法进行排序。排序到子表只有一个元素时结束。

【算法实现】

void QSort(SqList &L,int low,int high){
    if(low<high){  //长度大于1
        pivotloc = Partition(L,low,high);  //进行排序，得出中心元素
        QSort(L,low,pivotlor-1); //递归左子表
        QSort(L,pivotloc+1,high); //递归右子表
    }
}
//排序方法
int Partition(SqList &L,int low,int high){
    L.r[0] = L.r[low];  //存放存放第一个元素到哨兵作为中心元素
    pivotkey = L.r[low].key; //存放第一个关键字值
    while(low<high){  //low
        //从后面部分开始处理
        while(low < high && L.r[high].key >=pivotkey) --high;  //如果右边元素大于中心元素，指针往前进一位
        L.r[low] = L.r[high];  //如果右边元素小于中心元素，放到前面
        //现在指向前面部分
        while(low < high && L.[low].key <= pivotkey) ++low;  //如果左边元素小于中心元素，指针往后进一位
        L.r[high] = L.r[low]; //如果左边元素大于中心元素，放到后面
    }
    L.r[low] = L.r[0];
    return low;
}

【算法分析】

• 平均情况下时间复杂度O(n log2 n)，最坏情况下时间复杂度O(n²)

• 就平均计算时间而言，快速排序是本章节讨论的所有内排序方法中最好的一个。

• 快速排序不是原地排序。程序使用了递归，而递归调用需要用栈支持。所以平均情况下需要O(log n)的栈空间。

• 快速排序是一种不稳定的排序方法。

• 快速排序不适于队原本有序或基本有序的记录序列进行排序。

8.4选择排序

8.4.1简单(直接)选择排序

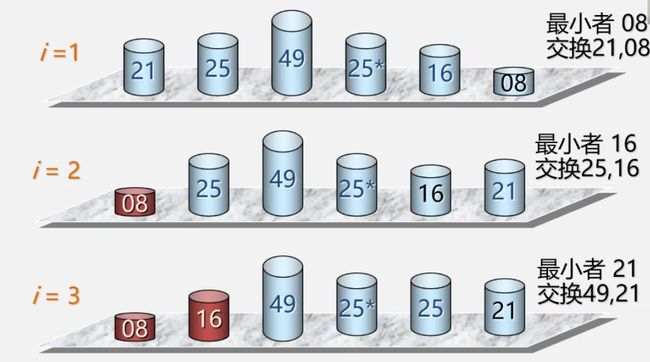
【算法思想】待排序的数据中选最大（最小）的元素放在其最终位置。

基本操作（从小到大排序）：

①通过n-1次关键字比较，从n个记录中找出关键字最小的关键字，将它与第一个记录交换。

②除去第一个记录，通过n-2次关键字比较，从n-1个记录中找出关键字最小的关键字，将它与第二个记录交换。

③依次类推，进行n-1躺排序后，排序结束。

【例】

【算法实现】

void SelectSort(SqList &K){
    for(i=1;i<L.length;i++){
        k=i;
        for(j=i+1;j<=L.length;j++){
            if(L.r[j].key < L.r[k].key) k=j; //记录最小值的位置
        }
        if(k!=i)
            swap(L.r[i],L.r[k]);//交换L.r[i]和L.r[k]
    }
}

【算法分析】

• 最好、最坏、平均时间复杂度O(n²)
• 简单选择排序是一个不稳定的算法。

8.4.2堆排序

• 堆定义：

从堆的定义来看，堆的性质满足完全二叉树。

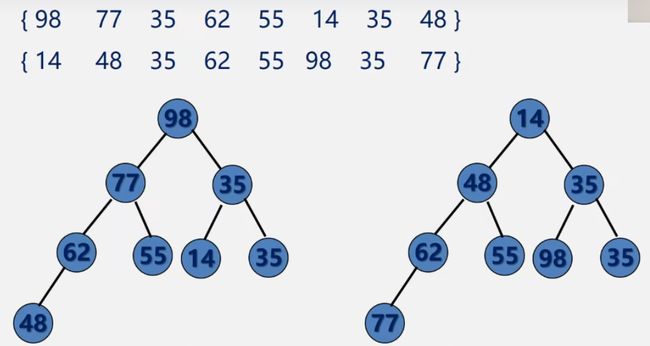
• 如何判断是不是堆：将元素放到一棵完全二叉树当中，如果符合堆大小定义，则是堆。

可以看出图中图一是大根堆，图二是小根堆。

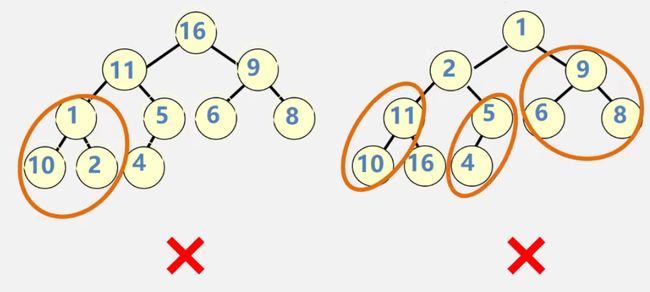
可以看出两图都不是根堆。

【小根堆调整】

①输出栈顶元素之后，以堆中最后一个元素代替。

②然后将根结点与左、右子树根结点值进行比较，与其中小值进行交换。

③重复上述操作直到叶子结点，得到新的堆。称这个从堆顶到叶子的调整过程为“筛选”。

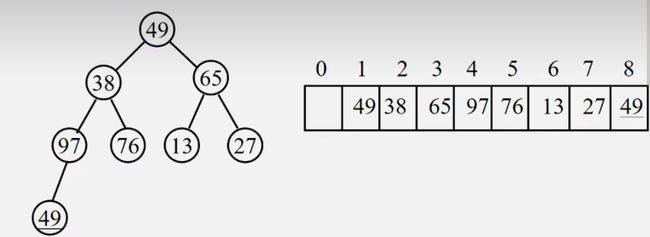
【例】将这个小根堆输出栈顶元素。

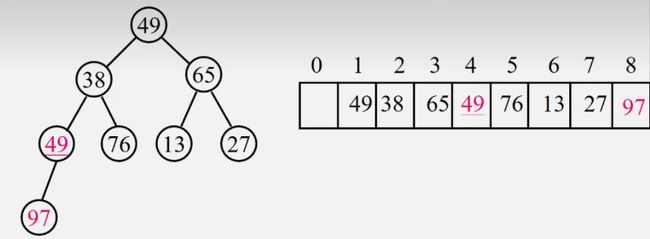
①输出根并用最后一个元素代替。

②将新的根比较左右孩子值大小，与值比较小的进行交换

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DIIwM4Kt-1691835501235)(F:/%E6%A1%8C%E9%9D%A2%E6%96%87%E4%BB%B6/%E7%BC%96%E7%A8%8B%E5%AD%A6%E4%B9%A0/img/image-20230807180758287-169183534932067.png)]

③继续与左右孩子值大小，与值比较小的进行交换

• 对于一个无序序列进行反复筛选，也就是反复调整，就可以得到一个堆。

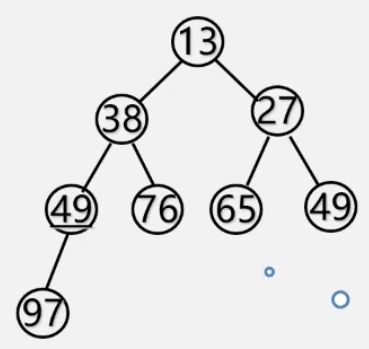
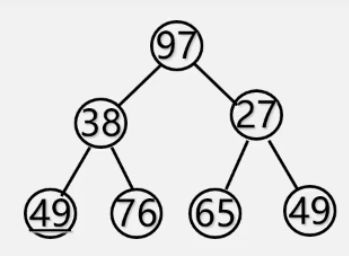
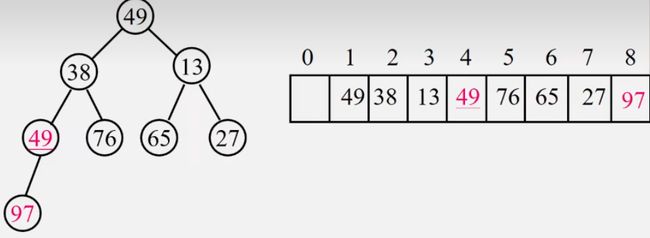
【例】有关键字49,38,65,97,76,13,27,49的一组记录，将其按照关键字调整为一个小根堆。

①初始

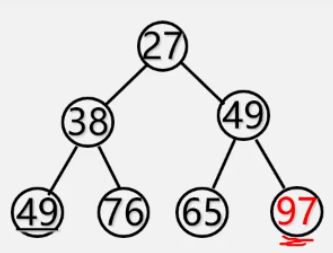
②第一次调整，最后的49不符合小根堆的定义，将49与它的根结点97进行交换

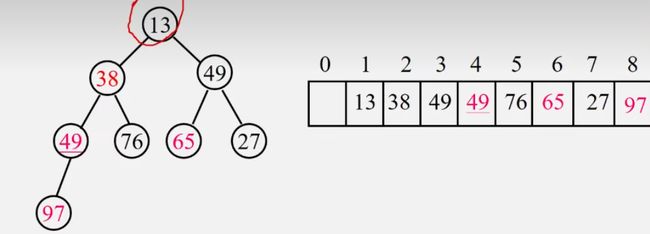
②第二次调整，13不符合小根堆定义，将13与它的根结点65进行交换。

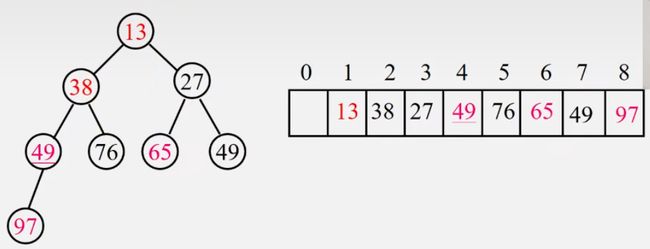
③第三次调整，13不符合小根堆定义，将13与它根结点49进行交换

④第四次调整，27不符合小根堆的定义，将27与它的根结点49进行交换

得到小根堆。

• 堆排序：若堆一个无序序列建堆，然后输出根。重复该过程就可以由一个无序序列输出有序序列。

【算法实现】

void HeapSort(elem R[]){
    int i;
    for(i=n/2;i>=1;i--)
        HeapAdjust(R,i,n);//建立初始堆
    for(i=n;i>1;i--){ //进行n-1趟排序
        Swap(R[1],R[i]); //根与最后一个元素交换
        HeapAdjust(R,1,i-1); //对R[1]到R[i-1]重新建堆
    }
}

//建堆
void HeapAdjust(elem R[],int s,int m){
    rc=R[s];
    for(j=2*s;j<=m;k*=2){
        if(j<m && R[j]<R[j+1]) ++j;
        if(rc>=R[j]) break;
        R[s] = R[j];
        s=j;
    }
    R[s] = rc;
}

【算法分析】

• 堆排序的时间复杂度O(n log2 n)

8.5归并排序

• 基本思想：将两个或两个以上有序子序列，归并为一个有序序列。
• 在内部排序中，一般采用2-路归并排序。

【例】

整个归并排序仅需⌈log2 n⌉趟

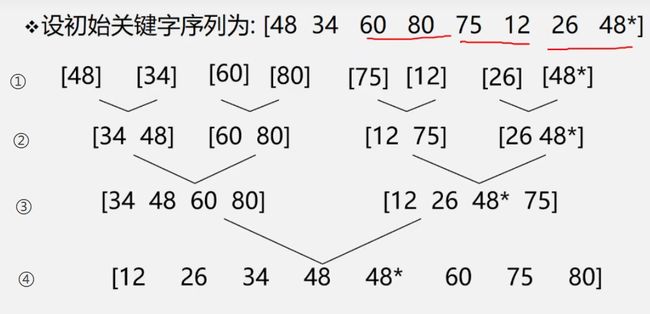
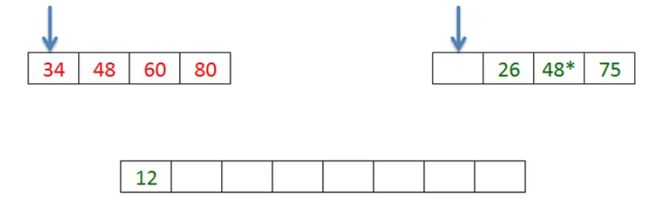
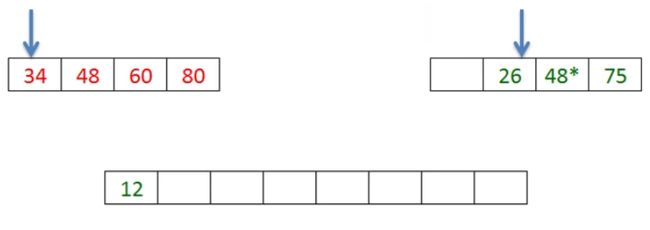
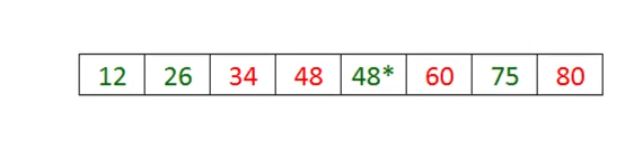
【例子】关键：如何将两个有序序列合成一个有序序列

主要从第一个结点做标记。比较两个有序序列谁比较小，放到新的数组当中，然后标记往后一位。

①13比34小，先进入新数组

②26比34小先进入到新数组。

③以此类推，合并称一个有序序列。

【算法分析】

• 时间复杂度O(n log2 n)
• 空间复杂度O(n)
• 这是一个稳定的算法

8.6基数排序

【算法思想】

数字是有范围的，均由0-9组成。相继按照个、十、百……进行排序。

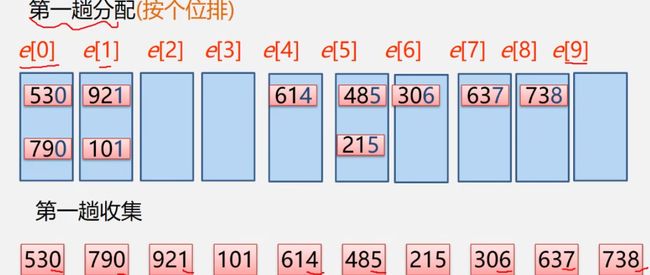
【例】614,738,921,485,637,101,215,530,790,306

①第一趟按照个位的大小进行排序

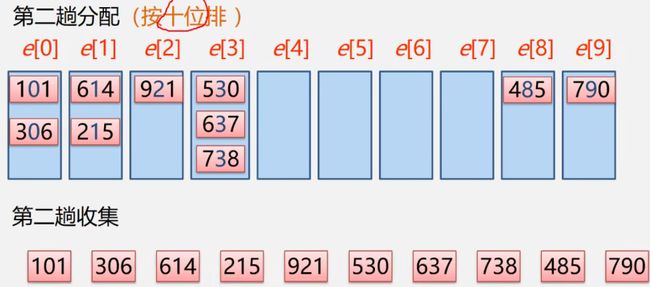
②按照第一趟排序，按照十位的大小进行排序

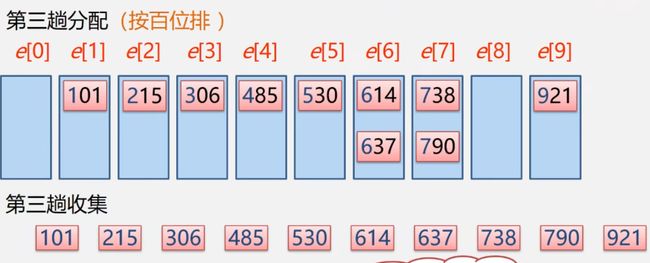
③按照第二趟排序，按照百位大小进行排序

【算法分析】

• 时间复杂度O(k * (n+m) )。其中k为关键字个数，m为关键字取值范围个数。
• 这是一个稳定的算法

8.7内部排序总结

• 按照时间性能：

1.时间复杂度为O(n logn)：快速排序、堆排序、归并排序，其中快速排序最好

2.时间复杂度为O(n²)：直接插入排序、冒泡排序、简单选择排序，其中直接插入排序最好。

3.时间复杂度O(n)：基数排序

• 按照空间性能：

1.空间复杂度O(1)：所有简单排序方法，如插入排序、冒泡排序、简单选择排序和堆排序

2.快速排序为O(log n)，为栈所需的辅助空间

3.归并排序所需最多，空间复杂度为O(n)

、百……进行排序。

【例】614,738,921,485,637,101,215,530,790,306

①第一趟按照个位的大小进行排序

[外链图片转存中…(img-ego8fGvJ-1691835501238)]

②按照第一趟排序，按照十位的大小进行排序

[外链图片转存中…(img-zM2sTuhd-1691835501238)]

③按照第二趟排序，按照百位大小进行排序

[外链图片转存中…(img-TXJ7mDp6-1691835501238)]

【算法分析】

• 时间复杂度O(k * (n+m) )。其中k为关键字个数，m为关键字取值范围个数。
• 这是一个稳定的算法

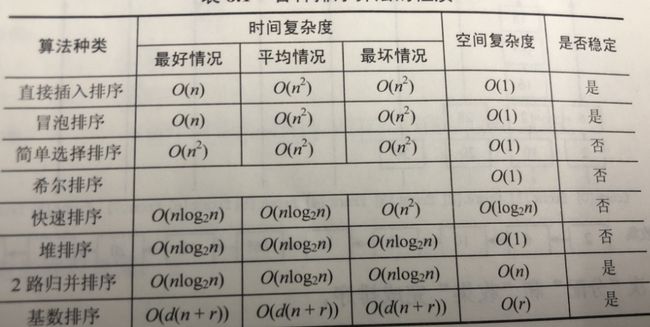
8.7内部排序总结

[外链图片转存中…(img-BbLoPkXf-1691835501238)]

• 按照时间性能：

1.时间复杂度为O(n logn)：快速排序、堆排序、归并排序，其中快速排序最好

2.时间复杂度为O(n²)：直接插入排序、冒泡排序、简单选择排序，其中直接插入排序最好。

3.时间复杂度O(n)：基数排序

• 按照空间性能：

1.空间复杂度O(1)：所有简单排序方法，如插入排序、冒泡排序、简单选择排序和堆排序

2.快速排序为O(log n)，为栈所需的辅助空间

3.归并排序所需最多，空间复杂度为O(n)

• 每次遍历至少有一个在最终位置上：冒泡排序、简单选择排序。

学习视频：数据结构——王卓；
参考文献：数据机构C语言版第2班——严蔚敏