红黑树
一、红黑树性质
一棵二叉查找树如果满足下面的红黑性质,则为一棵红黑树:
1) 每个结点或是红的,或是黑的。
2) 根节点是黑的。
3) 每个叶结点(NIL)是黑的。
4) 如果一个结点是红的,则它的两个儿子都是黑的。
5) 对于每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
引理:一棵有n个内结点的红黑树的高度至多为2log2(n+1)。
二、旋转
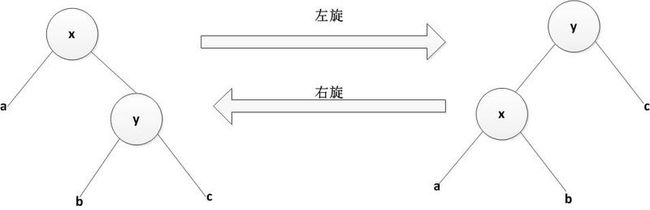
左旋以x到y之间的链为“支轴”进行。它使y成为该子树新的根,x成为y的左孩子,而y的左孩子成为x的右孩子。
左旋的伪代码如下:
1 LEFT-ROTATE(T,x) 2 y <- right[x] ;Set y 3 right[x] <- left[y] ;Turn y's left subtree into x's right subtree 4 if left[y]!=NIL[T] 5 then p[left[y]] <- x 6 p[y] <- p[x] ;Link x's parent to y 7 if p[x]=NIL[T] 8 root[T] <-y 9 else if x=left[p[x]] 10 left[p[x]] <- y 11 else right[p[x]] <-y 12 left[y] <- x 13 p[x] <-y
旋转示意图如下:
代码如下:
1 enum RB_Color 2 { 3 RED, 4 BLACK 5 }; 6 7 struct RB_Tree 8 { 9 int key; 10 RB_Tree *Left; 11 RB_Tree *Right; 12 RB_Tree *Parent; 13 RB_Color Color; 14 }; 15 16 /*红黑树左旋操作 17 操作步骤: 18 1.以e与R[e]之间的链为“支轴”进行。 19 2.使得R[e]成为该子树新的根,e成为R[e]的左孩子,而R[e]的左孩子则成为x的右孩子。 20 */ 21 void LEFT_ROTATE(RB_Tree * &root,RB_Tree *e,RB_Tree *NIL) 22 { 23 if(root==NIL||e==NIL) 24 return ; 25 //得到结点的右子结点 26 RB_Tree * RightChild=(*e).Right; 27 //把右子结点的左子结点赋值给结点右子结点 28 (*e).Right=(*RightChild).Left; 29 //如果右子结点的左子结点不为空,把其指向此结点 30 if((*RightChild).Left!=NIL) 31 (*((*RightChild).Left)).Parent=e; 32 //此结点的右子结点的父节点指向此节点的父节点 33 (*RightChild).Parent=(*e).Parent; 34 if((*e).Parent==NIL) 35 root=RightChild; 36 else if(e==(*((*e).Parent)).Left) 37 (*((*e).Parent)).Left=RightChild; 38 else 39 (*((*e).Parent)).Right=RightChild; 40 //把此节点放到其右结点的左结点上 41 (*RightChild).Left=e; 42 //把此节点的父节点指向其右结点 43 (*e).Parent=RightChild; 44 } 45 46 /* 47 红黑树的右旋操作 48 */ 49 void RIGHT_ROTATE(RB_Tree * &root,RB_Tree *e,RB_Tree *NIL) 50 { 51 if(root==NIL||e==NIL) 52 return ; 53 RB_Tree * LeftChild=(*e).Left; 54 (*e).Left=(*LeftChild).Right; 55 if((*LeftChild).Right!=NIL) 56 (*((*LeftChild).Right)).Parent=e; 57 (*LeftChild).Parent=(*e).Parent; 58 if((*e).Parent==NIL) 59 root=LeftChild; 60 else if(e==(*((*e).Parent)).Left) 61 (*((*e).Parent)).Left=LeftChild; 62 else 63 (*((*e).Parent)).Right=LeftChild; 64 (*LeftChild).Right=e; 65 (*e).Parent=LeftChild; 66 }
三、插入
首先,看一下插入伪代码,与二叉查找树树类似:
BR-INSERT(T,x) y <-NIL x <-root[T] while x!=NIL do y <- x if key[z] < key[x] then x <- left[x] else x <- right[x] p[z] <-y if y=NIL then root[T] <- z else if key[z] <key[y] then left[y] <- z else right[y] <-z left[z] <-NIL right[z] <-NIL color[z] <-RED RB-INSERT-FIXUP(T,x)
由于插入了一个红色的结点有可能会破坏红黑的性质。
性质1和性质3会继续保持,因为新插入的结点的子女都是哨兵NIL.性质5即从一个指定结点开始的每条路径上黑结点的个数都是相等的,也会成立,因为结点z代替了哨兵,并且结点z本身是具有哨兵的子女的红结点。因此,唯一可能被破坏的就是根节点需要为黑色的性质2,以及一个红结点不能有红子女的性质4。如果z是根节点则破坏了性质2,如果z的父节点是红色就破坏了性质4。例如下图破坏了性质4。
插入结点z后,破坏了红黑树的性质4.具体的处理方法分为以下三类:
情况1:z的叔叔y是红色的。如上图所示。这种情况的处理方法wie,把插入结点(z)的父节点和叔父结点设置为黑色,然后z指针上移两层,指向其祖先结点,并把新指向的结点变为红色,递归处理新指向的结点。如下图所示。
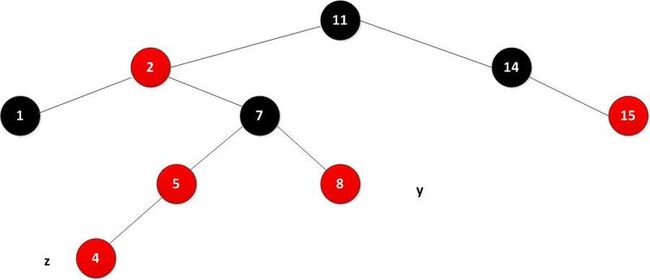
第二种情况:z的叔叔y是黑色的,而且z是右孩子,如上图所示。
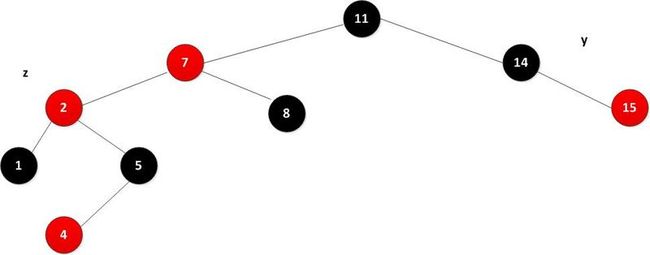
通过一次左旋,变成第三种情况,左旋后如下图所示。
第三种情况:z的叔叔y是黑色的,而且z是左孩子,如上图。
程序源代码如下:
1 /* 2 保持红黑树的性质 3 */ 4 void RB_INSERT_FIXUP(RB_Tree *&root,RB_Tree *e,RB_Tree *NIL) 5 { 6 RB_Tree * uncle=NIL; 7 while ((*((*e).Parent)).Color==RED) 8 { 9 //如果结点的父节点为其祖先结点的左孩子 10 if((*e).Parent==(*(*((*e).Parent)).Parent).Left) 11 uncle=(*(*((*e).Parent)).Parent).Right; //获得其叔父结点 12 else 13 uncle=(*((*e).Parent)).Left; 14 //如果其叔父结点为红色 15 if((*uncle).Color==RED) 16 { 17 (*((*e).Parent)).Color=BLACK; 18 (*uncle).Color=BLACK; 19 (*(*((*e).Parent)).Parent).Color=RED; 20 e=(*((*e).Parent)).Parent; 21 } 22 //其叔父为黑色, 23 else 24 { 25 //此结点为其父节点的右子结点 26 if(e==(*((*e).Parent)).Right) 27 { 28 e=(*e).Parent; 29 LEFT_ROTATE(root,e,NIL); 30 } 31 (*((*e).Parent)).Color=BLACK; 32 (*(*((*e).Parent)).Parent).Color=RED; 33 RIGHT_ROTATE(root,(*((*e).Parent)).Parent,NIL); 34 } 35 } 36 (*root).Color=BLACK; 37 } 38 39 /* 40 向红黑树中插入元素 41 */ 42 void RB_INSERT(RB_Tree *&root,RB_Tree *e,RB_Tree *NIL) 43 { 44 if(e==NIL) 45 return ; 46 RB_Tree * parent=NIL; 47 RB_Tree *current=root; 48 while (current!=NIL) 49 { 50 parent=current; 51 if((*current).key<(*e).key) 52 current=(*current).Right; 53 else 54 current=(*current).Left; 55 } 56 (*e).Parent=parent; 57 if(parent==NIL) 58 root=e; 59 else 60 { 61 if((*e).key<(*parent).key) 62 (*parent).Left=e; 63 else 64 (*parent).Right=e; 65 } 66 (*e).Left=NIL; 67 (*e).Right=NIL; 68 (*e).Color=RED; 69 RB_INSERT_FIXUP(root,e,NIL); 70 71 }
测试结果如图: