python机器学习
文章目录
- 机器学习
- 1. sklearn库
-
- 1.1 使用sklearn库提供的数据集
- 1.2 数据集的划分
- 1.3 特征工程
-
- 1.3.1 特征抽取
-
- 1.3.1.1字典特征提取:类别-> one-hot编码
- 1.3.1.2 文本特征抽取
- 1.3.2 特征预处理
-
- 1.3.2.1 归一化
- 1.3.2.2 标准化
- 1.3.3 特征降维
-
- 1.3.3.1 特征选择
-
- 1.3.3.1.1 低方差特征过滤
- 1.3.3.1.2 相关系数
- 1.3.3.2 主成分分析PCA
- 2. 分类算法
-
- 2.1 sklearn转换器和预估器
- 2.2 KNN算法
- 2.3 模型选择与调优
-
- 2.3.1 交叉验证
- 2.3.2 超参数搜索 - 网格搜索(Grid Search)
- 2.4 朴素贝叶斯算法
- 2.5 决策树
- 2.6 随机森林
- 3. 回归与聚类算法
-
- 3.1 线性回归
- 3.2 欠拟合与过拟合
- 3.3 岭回归—线性回归的改进
- 3.4 逻辑回归与二分类(分类算法)
- 3.5 模型保存与加载
- 3.6 无监督学习K-means
机器学习
- 机器学习是从数据中自动分析获得模型,并利用模型对未知数据进行预测。
- 机器学习要学习的数据称为数据集,数据集由特征值和目标值构成,每个样本一般包含多个特征值和一个目标值,多个特征值相互影响构成目标值,有的样本也可以没有目标值
- 机器学习算法分类:
有目标值 -> 监督学习:
目标值是类别 -> 分类问题 :k-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归
目标值是连续型的数据 ->回归问题:线性回归、岭回归
没有目标值 -> 无监督学习:聚类k-means - 机器学习开发流程:获取数据 - 数据处理 - 特征工程(进一步处理)- 机器学习算法训练 - 得到模型 - 模型评估(不好则跳到数据处理) - 应用
- 学习阶段可使用的数据集:sklearn库自带数据集、kaggle、UCI
1. sklearn库
1.1 使用sklearn库提供的数据集
# 获取小规模数据集,数据包含在datasets里,*是数据集的名称
sklearn.datasets.load_*()
# 获取大规模数据集,需要从网络上下载,函数的第一个参数表示数据集下载到的目录,默认是~/scikit_learn_data/
sklearn.datasets.fetch_*(data_home=None)
load和fetch返回的数据类型是继承自字典的一个类,包含了5个键

from sklearn.datasets import load_iris
def datasets_demo():
# 获取数据集
iris = load_iris()
print("鸢尾花数据集:\n",iris)
print("查看数据集描述:\n",iris['DESCR'])
print("查看特征值的名字:\n",iris.feature_names)
print("查看特征值:\n",iris.data,iris.data.shape)
print("查看标签名:\n",iris.target_names)
print("查看标签数组:\n",iris.target)
return None
if __name__ == "__main__":
datasets_demo()
1.2 数据集的划分
机器学习的数据集一般会划分为两个部分:
- 训练数据:用于训练,构建模型
- 测试数据:在模型检验时使用,用于评估模型是否有效,测试数据一般占数据集的20%-30%
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def datasets_demo():
# 获取数据集
iris = load_iris()
# 数据集划分
# 返回训练集特征值,测试集特征值,训练集目标值,测试集目标值
x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target,test_size=0.2,random_state=22)
print("训练集特征值:\n",x_train)
return None
if __name__ == "__main__":
datasets_demo()
1.3 特征工程
特征工程是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用的过程,特征工程包含特征抽取、特征预处理、特征降维
1.3.1 特征抽取
特征提取:将文本类型或者其他数据类型转化成可用于机器学习的数字特征,使用sklearn.feature_extraction
1.3.1.1字典特征提取:类别-> one-hot编码
from sklearn.feature_extraction import DictVectorizer
def dict_demo():
# 字典特征提取
data = [{'city':'北京','temperature':'100'},
{'city':'上海','temperature':'60'},
{'city':'深圳','temperature':'30'}
]
# 1.实例化一个转换器类
# sparse参数默认为True,即返回结果是稀疏矩阵,表示出非零元素的位置,
# 当类别特别多时(如果用二维数组表示的话0会特别多)有助于节省内存,设置为False的话返回的是二维数组
transfer = DictVectorizer(sparse=False)
# 2.调用fit_transform()
data_new = transfer.fit_transform(data)
print("data_new:\n",data_new)
# 查看各类别的名称
print("特征名字:",transfer.get_feature_names())
if __name__ == "__main__":
dict_demo()
稀疏矩阵的表示形式:

二维数组的表示形式:
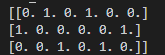
特征抽取的应用场景:
数据集中类别特征比较多时,将数据集的特征转化为字典类型,然后用DictVectorizer转化
1.3.1.2 文本特征抽取
把一篇文章进行分类可以把句子、短语、单词或者字母作为特征,一般用单词作为特征,也就是把单词作为特征词,特征词构成特征

其中的参数stop_words是一个列表,排除一些对我们统计没有作用的词,网络上会有一些做自然语言统计的停用词表
方法一:sklearn.feature_extraction.text.CountVectorizer
from sklearn.feature_extraction.text import CountVectorizer
def count_demo():
# 文本特征抽取
data = ["life is short,i like like python","life is too long, i dislike python"]
# 1.实例化一个转换器类
# CountVectorizer没有sparse参数,所以返回的是稀疏矩阵
transfer = CountVectorizer()
# 2.调用fit_transform()
data_new = transfer.fit_transform(data)
print("特征名字:",transfer.get_feature_names())
print("data_new:\n",data_new)
# 我们也可以使用转换后的对象的toarray方法,同样可以输出二维数组
print("data_new:\n",data_new.toarray())
if __name__ == "__main__":
count_demo()
结果:
特征名字: ['dislike', 'is', 'life', 'like', 'long', 'python', 'short', 'too']
data_new:
(0, 2) 1
(0, 1) 1
(0, 6) 1
(0, 3) 2
(0, 5) 1
(1, 2) 1
(1, 1) 1
(1, 5) 1
(1, 7) 1
(1, 4) 1
(1, 0) 1
data_new:
[[0 1 1 2 0 1 1 0]
[1 1 1 0 1 1 0 1]]
可以知道使用CountVectorizer来进行文本特征抽取的方法是统计每一个样本出现特征词的次数
from sklearn.feature_extraction.text import CountVectorizer
def countChinese_demo():
# 中文文本特征抽取
# 由于中文特性,我们需要增加空格手动分词,或者使用jieba分词库或者其他工具
data = ["我 爱 北京 天安门","天安门 上 太阳 升"]
# 1.实例化一个转换器类
# CountVectorizer没有sparse参数,所以返回的是稀疏矩阵
transfer = CountVectorizer()
# 2.调用fit_transform()
data_new = transfer.fit_transform(data)
print("特征名字:",transfer.get_feature_names())
print("data_new:\n",data_new)
# 我们也可以使用转换后的对象的toarray方法,同样可以输出二维数组
print("data_new:\n",data_new.toarray())
if __name__ == "__main__":
countChinese_demo()
结果:
特征名字: ['北京', '天安门', '太阳']
data_new:
(0, 0) 1
(0, 1) 1
(1, 1) 1
(1, 2) 1
data_new:
[[1 1 0]
[0 1 1]]
from sklearn.feature_extraction.text import CountVectorizer
import jieba
def cut_words(text):
# 进行中文分词
return " ".join(jieba.lcut(text))
def countChinese_demo2():
# 中文文本特征抽取
data = ["我爱北京天安门","天安门上太阳升"]
# 中文分词
data_new = []
for i in data:
data_new.append(cut_words(i))
# 1.实例化一个转换器类
# CountVectorizer没有sparse参数,所以返回的是稀疏矩阵
transfer = CountVectorizer()
# 2.调用fit_transform()
data_new = transfer.fit_transform(data_new)
print("特征名字:",transfer.get_feature_names())
print("data_new:\n",data_new)
# 我们也可以使用转换后的对象的toarray方法,同样可以输出二维数组
print("data_new:\n",data_new.toarray())
if __name__ == "__main__":
countChinese_demo2()
结果:
特征名字: ['北京', '天安门', '太阳升']
data_new:
(0, 0) 1
(0, 1) 1
(1, 1) 1
(1, 2) 1
data_new:
[[1 1 0]
[0 1 1]]
使用方法一进行特征提取,并不利于找到关键词,也就是说不利于找到在某种类别的文章中出现的频率高,在另外一种类别中出现的频率低这种词,因此就有了以下的方法二
方法二:sklearn.feature_extraction.text.TfidVectorizer


from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
def cut_words(text):
# 进行中文分词
return " ".join(jieba.lcut(text))
def tfidf_demo():
# 用TF-IDF的方法进行文本特征抽取
# 中文文本特征抽取
data = ["我爱北京北京天安门","天安门天安门上太阳升"]
# 中文分词
data_new = []
for i in data:
data_new.append(cut_words(i))
# 1.实例化一个转换器类
# CountVectorizer没有sparse参数,所以返回的是稀疏矩阵
transfer = TfidfVectorizer()
# 2.调用fit_transform()
data_new = transfer.fit_transform(data_new)
print("特征名字:",transfer.get_feature_names())
print("data_new:\n",data_new)
# 我们也可以使用转换后的对象的toarray方法,同样可以输出二维数组
print("data_new:\n",data_new.toarray())
if __name__ == "__main__":
tfidf_demo()
结果:
特征名字: ['北京', '天安门', '太阳升']
data_new:
(0, 1) 0.33517574332792605
(0, 0) 0.9421556246632359
(1, 2) 0.5749618667993135
(1, 1) 0.8181802073667197
data_new:
[[0.94215562 0.33517574 0. ]
[0. 0.81818021 0.57496187]]
二维数组中数值比较大的表示该词更重要,具有分类意义
tf-idf在分类机器学习算法中是一种重要的前期数据处理方式
1.3.2 特征预处理
特征预处理:通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
特征预处理经常用到的一种方式就是数值型数据的无量纲化,包括归一化和标准化,特征预处理的API在sklearn中有一个preprocessing类。之所以要进行无量纲化就是因为我们的特征值之间的量纲不统一(特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级),容易影响到目标结果,使得算法无法学习到其他的特征。
1.3.2.1 归一化
归一化就是通过对原始数据进行变换把数据映射到(默认为[0,1])之间
归一化的公式:

sklearn中的api:其中feature_range参数就是指定要把特征值映射到那个区间范围内

from sklearn.preprocessing import MinMaxScaler
import pandas
def minmax_demo():
# 归一化
# 1.获取数据
data = pandas.read_csv("D:\wampserver\www\code\machinelearning\data.txt")
# 对数据进行索引,取所有行和前三列
data = data.iloc[:,:3]
print(data)
# 2.实例化一个转换器类
transfer = MinMaxScaler()
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print("data_new:\n",data_new)
if __name__ == "__main__":
minmax_demo()
结果:
milage Liters Consumtime
0 40920 8.326976 0.953952
1 14488 7.153469 1.673904
2 26052 1.441871 0.805124
3 75136 13.147394 0.428964
4 38344 1.669788 0.134296
data_new:
[[0.43582641 0.58819286 0.53237967]
[0. 0.48794044 1. ]
[0.19067405 0. 0.43571351]
[1. 1. 0.19139157]
[0.3933518 0.01947089 0. ]]
1.3.2.2 标准化
归一化是根据最大值和最小值求出来的,如果最大值或最小值是异常值的话,那么结果容易受到影响,不是很准确,只适合传统精确小数据场景。一种更为通用的方法是标准化。
标准化是通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内
标准化的公式为:


sklearn中的api:

from sklearn.preprocessing import StandardScaler
import pandas
def stand_demo():
# 标准化
# 1.获取数据
data = pandas.read_csv("D:\wampserver\www\code\machinelearning\data.txt")
# 对数据进行索引,取所有行和前三列
data = data.iloc[:,:3]
print(data)
# 2.实例化一个转换器类
transfer = StandardScaler()
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print("data_new:\n",data_new)
if __name__ == "__main__":
stand_demo()
结果:
milage Liters Consumtime
0 40920 8.326976 0.953952
1 14488 7.153469 1.673904
2 26052 1.441871 0.805124
3 75136 13.147394 0.428964
4 38344 1.669788 0.134296
data_new:
[[ 0.0947602 0.44990013 0.29573441]
[-1.20166916 0.18312874 1.67200507]
[-0.63448132 -1.11527928 0.01123265]
[ 1.77297701 1.54571769 -0.70784025]
[-0.03158673 -1.06346729 -1.27113187]]
标准化在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景
1.3.3 特征降维
降维是值在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程。
1.3.3.1 特征选择
特征选择就是从包含冗余或相关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征
两类方法:

其中相关系数法就是通过横向某两个特征之间是否有很强的相关性,然后进行过滤的方法
相关的api在sklearn.feature_selection中可以找到
1.3.3.1.1 低方差特征过滤
低方差的特征数据说明大多样本的值比较相近,这样的特征意义就不大,可以过滤掉
from sklearn.feature_selection import VarianceThreshold
import pandas
def variance_demo():
# 过滤低方差特征
# 1.获取数据
data = pandas.read_csv("D:\\wampserver\\www\\code\\machinelearning\\factor_returns.csv")
data = data.iloc[:,1:-2]
# 2.实例化一个转换器类
transfer = VarianceThreshold(threshold=5)
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print(data_new,data_new.shape)
if __name__ == "__main__":
variance_demo()
结果:原来特征有9个,过滤掉特征值方差低于5的特征后剩下8个特征
[[ 5.95720000e+00 1.18180000e+00 8.52525509e+10 ... 1.21144486e+12
2.07014010e+10 1.08825400e+10]
[ 7.02890000e+00 1.58800000e+00 8.41133582e+10 ... 3.00252062e+11
2.93083692e+10 2.37834769e+10]
[-2.62746100e+02 7.00030000e+00 5.17045520e+08 ... 7.70517753e+08
1.16798290e+07 1.20300800e+07]
...
[ 3.95523000e+01 4.00520000e+00 1.70243430e+10 ... 2.42081699e+10
1.78908166e+10 1.74929478e+10]
[ 5.25408000e+01 2.46460000e+00 3.28790988e+10 ... 3.88380258e+10
6.46539204e+09 6.00900728e+09]
[ 1.42203000e+01 1.41030000e+00 5.91108572e+10 ... 2.02066110e+11
4.50987171e+10 4.13284212e+10]] (2318, 8)
1.3.3.1.2 相关系数
from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
import pandas
def variance_demo():
# 过滤低方差特征
# 1.获取数据
data = pandas.read_csv("D:\\wampserver\\www\\code\\machinelearning\\factor_returns.csv")
data = data.iloc[:,1:-2]
# 2.实例化一个转换器类
transfer = VarianceThreshold(threshold=5)
# 3.调用fit_transform
data_new = transfer.fit_transform(data)
print(data_new,data_new.shape)
# 计算某两个变量之间的相关系数
r= pearsonr(data["pe_ratio"],data["pb_ratio"])
print("相关系数:",r)
if __name__ == "__main__":
variance_demo()
结果:
[[ 5.95720000e+00 1.18180000e+00 8.52525509e+10 ... 1.21144486e+12
2.07014010e+10 1.08825400e+10]
[ 7.02890000e+00 1.58800000e+00 8.41133582e+10 ... 3.00252062e+11
2.93083692e+10 2.37834769e+10]
[-2.62746100e+02 7.00030000e+00 5.17045520e+08 ... 7.70517753e+08
1.16798290e+07 1.20300800e+07]
...
[ 3.95523000e+01 4.00520000e+00 1.70243430e+10 ... 2.42081699e+10
1.78908166e+10 1.74929478e+10]
[ 5.25408000e+01 2.46460000e+00 3.28790988e+10 ... 3.88380258e+10
6.46539204e+09 6.00900728e+09]
[ 1.42203000e+01 1.41030000e+00 5.91108572e+10 ... 2.02066110e+11
4.50987171e+10 4.13284212e+10]] (2318, 8)
相关系数: (-0.004389322779936271, 0.8327205496564927)
当遇到特征与特征之间相关性很高,可以选取其中一个作为代表,或者进行加权求和形成一个新的特征
1.3.3.2 主成分分析PCA
from sklearn.decomposition import PCA
def pca_demo():
# PCA降维
data = [[2,8,4,5],[6,3,0,8],[5,4,9,1]]
# 1.实例化一个转换器类
# 4个特征转换成两个特征
transfer = PCA(n_components=2)
# 2.调用fit_transform
data_new = transfer.fit_transform(data)
print("data_new:\n",data_new)
if __name__ == "__main__":
pca_demo()
结果:
data_new:
[[ 1.28620952e-15 3.82970843e+00]
[ 5.74456265e+00 -1.91485422e+00]
[-5.74456265e+00 -1.91485422e+00]]
2. 分类算法
2.1 sklearn转换器和预估器
转换器 - 特征工程的父类:

估计器 - sklearn机器学习算法的实现

估计器工作流程:
- 实例化一个estimator
- 调用fit(x_train,y_train)方法,把训练集的特征值和目标值传进去,进行计算,生成模型
- 模型评估:(1)直接比对真实值和预测值,使用y_predict = predict(x_test),将测试集传进去后,获得预测值y_predict,比对真实值跟预测值y_test == y_predict
(2)计算准确率,调用estimator.score(x_test,y_test),传入测试集的特征值跟目标值
2.2 KNN算法
KNN算法的核心思想:根据“邻居”来推断出你的类别

除了欧式距离外常见的还有曼哈顿距离,也就是绝对值距离,即每个样本的各个特征值之差的绝对值之和;还有明可夫斯基距离。。
KNN算法的特点:如果k值取得过大 ,容易受到样本不均衡的影响,k值取得过小,容易受到异常点的影响,在使用KNN算法之前,要对数据进行无量纲化的处理
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
def knn_iris():
# 用knn算法对鸢尾花进行分类
# 1.获取数据
iris = load_iris()
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=6)
# 3.特征工程 对训练集和测试集标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
# 注意fit_transform其实是分为fit和transform两个方法,fit在按照标准化的公式进行计算
# 而transform在进行数据的转化,因此对测试集进行标准化时要调用的是transform方法,要对
# 数据集和测试集按照一个标准来转化,利用训练集的平均值和标准差进行转化
x_test = transfer.transform(x_test)
# 4.knn算法预估器
estimator = KNeighborsClassifier(n_neighbors=3)
estimator.fit(x_train,y_train)
# 5.模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n",y_predict==y_test)
# 方法2:计算准确率
score = estimator.score(x_test,y_test)
print("准确率为:\n",score)
if __name__ == "__main__":
knn_iris()
结果:
y_predict:
[0 2 0 0 2 1 1 0 2 1 2 1 2 2 1 1 2 1 1 0 0 2 0 0 1 1 1 2 0 1 0 1 0 0 1 2 1
2]
直接比对真实值和预测值:
[ True True True True True True False True True True True True
True True True False True True True True True True True True
True True True True True True True True True True False True
True True]
准确率为:
0.9210526315789473
KNN优点:简单、易于理解、易于实现、无需训练
KNN缺点:(1)必须指定K值,K值选择不当则分类精度不能保证(2)懒惰算法,对测试样本分类时的计算量大,内存开销大
使用场景:小数据场景,几千-几万样本,具体场景具体业务去测试
2.3 模型选择与调优
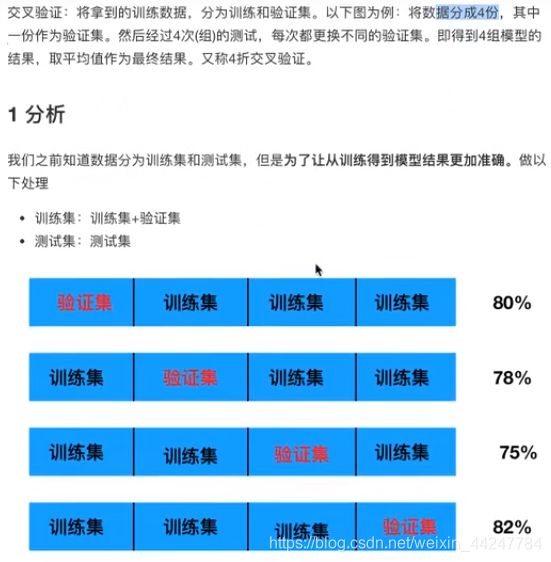
2.3.1 交叉验证
2.3.2 超参数搜索 - 网格搜索(Grid Search)
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
def knn_iris_gscv():
# 用knn算法对鸢尾花进行分类,添加网格搜索和交叉验证
# 1.获取数据
iris = load_iris()
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=22)
# 3.特征工程 对训练集和测试集标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.knn算法预估器
estimator = KNeighborsClassifier()
# 加入网格搜索与交叉验证
# 参数准备
param_dict = {"n_neighbors":[1,3,5,7,9,11]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=10)
estimator.fit(x_train,y_train)
# 5.模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n",y_predict==y_test)
# 方法2:计算准确率
score = estimator.score(x_test,y_test)
print("准确率为:\n",score)
# 打印调优后的相关结果
print("最佳参数:\n",estimator.best_params_)
print("最佳结果:\n",estimator.best_score_)
print("最佳估计器:\n",estimator.best_estimator_)
print("交叉验证结果:\n",estimator.cv_results_)
if __name__ == "__main__":
knn_iris_gscv()
结果:
y_predict:
[0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True True True True True True
True True True True True True False True True True True True
True True True True True True True True True True True True
True True]
准确率为:
0.9736842105263158
最佳参数:
{'n_neighbors': 3}
最佳结果:
0.9553030303030303
最佳估计器:
KNeighborsClassifier(n_neighbors=3)
交叉验证结果:
{'mean_fit_time': array([0.0007962 , 0.00099537, 0.00080218, 0.00089867, 0.00059495,
0.00089722]), 'std_fit_time': array([3.98402871e-04, 1.21931700e-05, 4.01227588e-04, 3.00211011e-04,
6.59621331e-04, 2.99518151e-04]), 'mean_score_time': array([0.00110178, 0.00139844, 0.00188742, 0.00199211, 0.00181341,
0.00139606]), 'std_score_time': array([0.00028558, 0.0006751 , 0.00083574, 0.00117104, 0.00040125,
0.00049545]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],
mask=[False, False, False, False, False, False],
fill_value='?',
dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([0.91666667, 0.91666667, 1. , 1. , 0.91666667,
0.91666667]), 'split1_test_score': array([1., 1., 1., 1., 1., 1.]), 'split2_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.90909091]), 'split3_test_score': array([0.90909091, 1. , 0.90909091, 0.90909091, 0.90909091,
1. ]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.90909091]), 'split6_test_score': array([0.90909091, 0.90909091, 0.90909091, 1. , 1. ,
1. ]), 'split7_test_score': array([0.90909091, 0.90909091, 0.81818182, 0.81818182, 0.81818182,
0.81818182]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([1., 1., 1., 1., 1., 1.]), 'mean_test_score': array([0.94621212, 0.95530303, 0.94545455, 0.95454545, 0.94621212,
0.95530303]), 'std_test_score': array([0.04397204, 0.0447483 , 0.06030227, 0.06098367, 0.05988683,
0.0604591 ]), 'rank_test_score': array([4, 1, 6, 3, 4, 1])}
其中正确率和最佳结果不一样,是因为准确率是整体的,是测试集的结果,而最佳结果是在训练集中,将训练集分为训练集和验证集,是验证集的结果
2.4 朴素贝叶斯算法

贝叶斯公式:

朴素贝叶斯算法是在贝叶斯公式下,假定了特征与特征之间相互独立。
朴素贝叶斯常用在文本分类上。

当样本量太少的时候,计算P(Fn|C)的时候可能会出现0,这样是不符合常理的,因此在计算P(Fn|C)的时候我们引入拉普拉斯平滑系数进行计算

api:

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def baye_demo():
# 朴素贝叶斯进行新闻分类
# 1.获取数据,sklearn自带的新闻数据集
news = fetch_20newsgroups('D:\wampserver\www\code\machinelearning',subset='all')
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(news.data,news.target)
# 3.特征工程:文本特征抽取
transfer = TfidfVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.朴素贝叶斯算法预估器流程
estimator = MultinomialNB()
estimator.fit(x_train,y_train)
# 5.模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n",y_predict==y_test)
# 方法2:计算准确率
score = estimator.score(x_test,y_test)
print("准确率为:\n",score)
# 打印调优后的相关结果
print("最佳参数:\n",estimator.best_params_)
print("最佳结果:\n",estimator.best_score_)
print("最佳估计器:\n",estimator.best_estimator_)
print("交叉验证结果:\n",estimator.cv_results_)
if __name__ == "__main__":
baye_demo()
结果:
y_predict:
[17 17 10 ... 15 1 10]
直接比对真实值和预测值:
[ True True True ... True True True]
准确率为:
0.8527164685908319
朴素贝叶斯优缺点:
![]()
2.5 决策树
决策树是一种树形结构,用以高效地进行决策,即如何确定查看特征的先后顺序以高效进行决策
了解决策树需要先理解一些信息论的知识:
- 信息是消除随机不定性的东西
- 衡量信息量 - 衡量消除的东西有多少 - 衡量消除的不确定性的大小 - >信息熵
当求出总的信息熵后 ,用它减去知道某个特征值后的信息熵(即条件熵)的差,就是信息增益,信息增益越大,特征值越重要,该特征值要看的顺序就越靠前


决策树的划分就不止信息增益,还有:

决策树api:参数criterion就是决策树的划分依据,max_depth是树的深度,如果不设置该参数的话,生成的决策树模型会尽可能拟合训练集的数据,这样的话可能会导致在测试集的表现不那么好,适当设置树的深度有可能会提高准确率

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
def decision_iris():
# 用决策树对鸢尾花进行分类
# 1.获取数据集
iris = load_iris()
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=22)
# 由于决策树不用计算距离,因此此处不用进行标准化
# 3.决策树预估器
estimator = DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train,y_train)
# 4.模型评估
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n",y_predict==y_test)
# 方法2:计算准确率
score = estimator.score(x_test,y_test)
print("准确率为:\n",score)
if __name__ == "__main__":
decision_iris()
结果:
y_predict:
[0 2 1 2 1 1 1 1 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 1 2 2 1 0 0 1 1 1 0 0
0]
直接比对真实值和预测值:
[ True True True True True True True False True True True True
True True True True True True False True True True True True
True True False True True False True True True True True True
True True]
准确率为:
0.8947368421052632
# 可视化决策树
export_graphviz(estimator,out_file="iris_tree.dot",feature_names = iris.feature_names)
然后会在当前目录下生成一个dot格式文件
digraph Tree {
node [shape=box] ;
0 [label="petal length (cm) <= 2.45\nentropy = 1.584\nsamples = 112\nvalue = [39, 37, 36]"] ;
1 [label="entropy = 0.0\nsamples = 39\nvalue = [39, 0, 0]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="petal width (cm) <= 1.75\nentropy = 1.0\nsamples = 73\nvalue = [0, 37, 36]"] ;
0 -> 2 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
3 [label="petal length (cm) <= 5.05\nentropy = 0.391\nsamples = 39\nvalue = [0, 36, 3]"] ;
2 -> 3 ;
4 [label="petal width (cm) <= 1.65\nentropy = 0.183\nsamples = 36\nvalue = [0, 35, 1]"] ;
3 -> 4 ;
5 [label="entropy = 0.0\nsamples = 34\nvalue = [0, 34, 0]"] ;
4 -> 5 ;
6 [label="sepal length (cm) <= 5.8\nentropy = 1.0\nsamples = 2\nvalue = [0, 1, 1]"] ;
4 -> 6 ;
7 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 0, 1]"] ;
6 -> 7 ;
8 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1, 0]"] ;
6 -> 8 ;
9 [label="petal width (cm) <= 1.55\nentropy = 0.918\nsamples = 3\nvalue = [0, 1, 2]"] ;
3 -> 9 ;
10 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 0, 2]"] ;
9 -> 10 ;
11 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1, 0]"] ;
9 -> 11 ;
12 [label="petal length (cm) <= 4.85\nentropy = 0.191\nsamples = 34\nvalue = [0, 1, 33]"] ;
2 -> 12 ;
13 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1, 0]"] ;
12 -> 13 ;
14 [label="entropy = 0.0\nsamples = 33\nvalue = [0, 0, 33]"] ;
12 -> 14 ;
}
在网站http://webgraphviz.com/能够将dot文件转化成树形结构:

决策树优缺点:

2.6 随机森林
集成学习方法:

随机森林是集成学习方法的一种。

随机森林的原理:采用bootstrap(有放回抽样)去选出用于建造每棵树的训练集,每个训练集的特征也是随机抽取的

api:

随机森林的优点:

3. 回归与聚类算法
3.1 线性回归
-
特征值与目标值之间建立了一个关系,这个关系可以理解为线性模型
-
线性回归当中线性模型有两种,一种是线性关系,另一种是非线性关系。
-
线性关系中单特征与目标值的关系呈直线关系,两个特征与目标值呈现平面的关系…
-
可以被称为线性模型的有自变量一次和参数一次的情况,因此线性模型也有可能是非线性关系的。
线性回归的思路是先假定一个线性模型,通过该线性模型计算出来的预测值跟真实值一定存在着误差,如果能够有某种方法能够使这种误差减少到0的话,那这个模型也就会变得准确。这个模型对应的参数也就是我们要求的参数。衡量预测值跟真实值之间的差距通过损失函数来实现。
损失函数:每个样本的预测值减去真实值的平方再求和

既然存在着损失,那就要去缩小损失,缩小损失又称为优化损失,需要用到优化算法
优化算法:常用的两种优化算法是正规方程和梯度下降,正规方程是直接用来求解模型的参数w,而梯度下降是通过不断试错改进来求得w。正规方程比较适合数据量小的情况


线性回归api:有两个,分别是用正规方程算法优化的和用梯度下降算法优化的

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
# 正规方程的优化方法对波士顿房价进行预测
# 1.获取数据
boston = load_boston()
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,random_state=22)
# 3.标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.预估器
estimator = LinearRegression()
estimator.fit(x_train,y_train)
# 5. 得出模型
print("正规方程优化方法:\n权重系数为:\n",estimator.coef_)
print("偏置为:\n",estimator.intercept_)
# 梯度下降的优化方法对波士顿房价进行预测
estimator = SGDRegressor()
estimator.fit(x_train,y_train)
# 5. 得出模型
print("梯度下降优化方法:\n权重系数为:\n",estimator.coef_)
print("偏置为:\n",estimator.intercept_)
结果:
正规方程优化方法:
权重系数为:
[-0.64817766 1.14673408 -0.05949444 0.74216553 -1.95515269 2.70902585
-0.07737374 -3.29889391 2.50267196 -1.85679269 -1.75044624 0.87341624
-3.91336869]
偏置为:
22.62137203166228
梯度下降优化方法:
权重系数为:
[-0.51893276 0.95534463 -0.46749722 0.79822562 -1.71942455 2.85300143
-0.16040978 -3.08783461 1.57211068 -0.89399149 -1.73330352 0.87299741
-3.93793452]
偏置为:
[22.62673772]
boston房价数据集中有13个特征值,对应的就有13个权重系数。
那么得到的两个模型如何才能知道哪个比较好呢?需要进行回归性能评估:
均方误差评价机制就是对每个样本拿预测值减去真实值再求平方,然后再求和取平均,哪个模型求得的均方误差比较小,这个模型就比较好一点

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
from sklearn.metrics import mean_squared_error
# 正规方程的优化方法对波士顿房价进行预测
# 1.获取数据
boston = load_boston()
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,random_state=22)
# 3.标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.预估器
estimator = LinearRegression()
estimator.fit(x_train,y_train)
# 5. 得出模型
print("正规方程优化方法:\n权重系数为:\n",estimator.coef_)
print("偏置为:\n",estimator.intercept_)
error = mean_squared_error(y_test,y_predict)
print("正规方程均方误差为:\n",error)
# 梯度下降的优化方法对波士顿房价进行预测
estimator = SGDRegressor()
estimator.fit(x_train,y_train)
# 5. 得出模型
print("梯度下降优化方法:\n权重系数为:\n",estimator.coef_)
print("偏置为:\n",estimator.intercept_)
# 6.模型评估
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test,y_predict)
print("梯度下降均方误差为:\n",error)
结果:
正规方程优化方法:
权重系数为:
[-0.64817766 1.14673408 -0.05949444 0.74216553 -1.95515269 2.70902585
-0.07737374 -3.29889391 2.50267196 -1.85679269 -1.75044624 0.87341624
-3.91336869]
偏置为:
22.62137203166228
正规方程均方误差为:
20.6275137630954
梯度下降优化方法:
权重系数为:
[-0.54320625 0.94259037 -0.40674915 0.77629639 -1.73922602 2.80134863
-0.13605652 -3.10891979 1.68737995 -1.0021945 -1.72699477 0.86706496
-3.91595837]
偏置为:
[22.63032362]
梯度下降均方误差为:
20.983136589997176
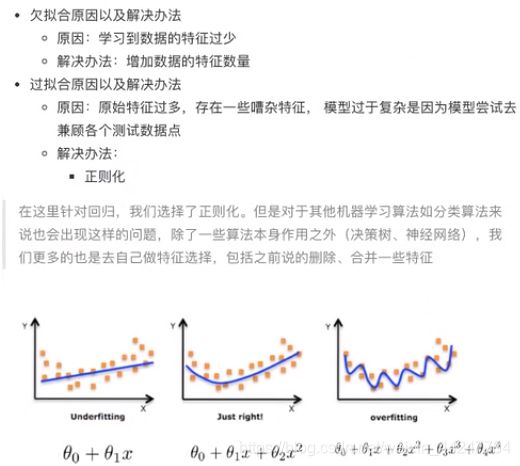
3.2 欠拟合与过拟合
3.3 岭回归—线性回归的改进
岭回归也是一种线性回归,只不过在算法建立回归方程的时候,加上L2正则化的限制,从而达到解决过拟合的效果。
api:

正则化力度越大,权重系数会越小,正则化力度越小,权重系数会越大
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
# 岭回归对波士顿房价进行预测
# 1.获取数据
boston = load_boston()
# 2.划分数据集
x_train,x_test,y_train,y_test = train_test_split(boston.data,boston.target,random_state=22)
# 3.标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4.预估器
estimator = Ridge()
estimator.fit(x_train,y_train)
# 5. 得出模型
print("岭回归:\n权重系数为:\n",estimator.coef_)
print("偏置为:\n",estimator.intercept_)
# 6.模型评估
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test,y_predict)
print("岭回归均方误差为:\n",error)
结果:
岭回归:
权重系数为:
[-0.63591916 1.12109181 -0.09319611 0.74628129 -1.91888749 2.71927719
-0.08590464 -3.25882705 2.41315949 -1.76930347 -1.74279405 0.87205004
-3.89758657]
偏置为:
22.62137203166228
岭回归均方误差为:
3.4 逻辑回归与二分类(分类算法)

逻辑回归是解决二分类问题(只有两种结果,是或者不是)的利器。
逻辑回归的输入就是一个线性回归的结果。要让这个线性回归的结果能够进行分类,还要将其带入一个激活函数sigmoid函数。
sigmoid = 1/(1+e^(-x)),将线性回归的输出代入x,以下是矩阵形式的表示
经过sigmoid函数后,能够将线性回归的输出映射到[0,1]区间内,将得到的值视为概率,规定超过某个值的话就说明该样本属于某个类别。
假设我们有一个线性回归y=w1x1+w2x2+w3x3+ … + wnxn +b,代入sigmoid函数得到我们的假设函数1/(1+e^(-(w1x1+w2x2+w3x3+ … + wnxn +b))),那么如何求出一组权重和偏置来使得我们这个模型能够准确地预测分类?初步的想法是想线性回归、岭回归那样构造损失函数,然后通过优化损失来求的权重和偏置。
但是之前构造的损失函数都需要通过每个样本的真实值和预测值去进行运算,而由于逻辑回归的真实值和预测值都是是否属于某个类别,不是一个数,因此不能像前面那样去求均方误差和最小二乘法了。这里要引入另外一种损失函数的构建方法。这里引入对数似然损失。

当y=1时,即真实值属于某个类别时,当经过sigmoid映射得到的值(横轴)(预测值)越接近1时,损失(纵轴)也就越小,当经过sigmoid映射得到的值越接近0时,损失就接近无穷大。
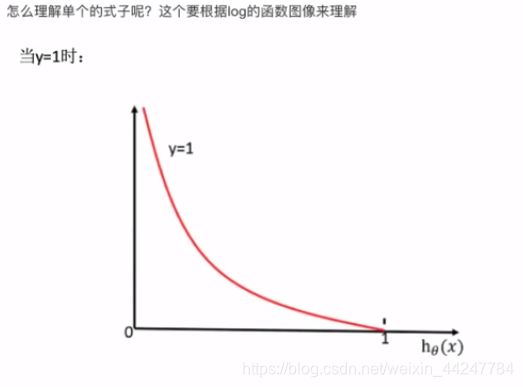
同理,当y=0时,即真实值不属于某个类别时,经过sigmoid映射得到的值越接近0,损失也就越小,经过sigmoid映射得到的值越接近1,损失也就越大

把公式结合起来写:其中yi是真实值

有了损失函数之后,就要优化损失,这里使用的也是梯度下降优化算法去减少损失函数的值,更新逻辑回归算法的权重参数,提升原本属于1类别的概率,降低原本是0类别的概率。
import pandas as pd
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 1.读取数据
path = "file:///D:/Users/lenovo/Desktop/python/Machine_Learning/Machine_Learning/resources/cancer/breast-cancer-wisconsin.data"
column_names = ['Sample code number','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion','Single Epithelial Cell Size',
'Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
data = pd.read_csv(path,names=column_names,index_col=False)
# 2.缺失值处理
# 1)替换?为np.nan
data.replace(to_replace="?",value=np.nan)
# 2)删除缺失样本
data.dropna(inplace=True)
# 验证是否还存在缺失值
# print(data.isnull().any())
# 3. 筛选特征值和目标值
x = data.iloc[:,1:-1]
y = data['Class']
# 4.划分数据集
x_train,x_test,y_train,y_test = train_test_split(x,y)
# 5.特征工程-标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 6.预估器流程
estimator = LogisticRegression()
estimator.fit(x_train,y_train)
# 7.逻辑回归的模型参数:回归系数和偏置
print(estimator.coef_)
print(estimator.intercept_)
# 8.模型评估
y_predict = estimator.predict(x_test)
print("y_predict:\n",y_predict)
print("直接比对真实值和预测值:\n",y_predict==y_test)
# 方法2:计算准确率
score = estimator.score(x_test,y_test)
print("准确率为:\n",score)
类似癌症等案例,我们评估模型,是要评估该模型预测一个人是否患癌症的准确性吗?显然这样的评估还不够好,我们想要的是在那些真实患癌症的人中,能够被该模型检测出来的概率,这就涉及到下面的召回率。
引入如下几个概念:
混淆矩阵:

精确率和召回率:
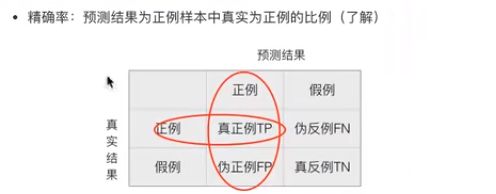

F1-score越高,模型越稳健

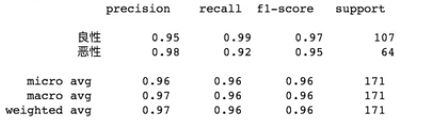
from sklearn.metrics import classification_report
report = classification_report(y_test,y_predict,labels=[2,4],target_names=['良性','恶性'])
print(report)
当样本不均衡时,如果要评估模型的时候,就需要用到ROC曲线和AUC指标


AUC即ROC曲线对x轴的面积,当计算出来的AUC小于0.5时,实际的AUC应为1-AUC

3.5 模型保存与加载
sklearn模型的保存和加载

保存的话就将模型的预估器序列化到本地,第一个参数就是预估器,第二个参数就是路径,文件后缀名为pkl
注意sklearn版本在0.21及一下才有joblib,可以直接使用安装第三方库joblib使用
import joblib
# 保存模型
joblib.dump(estimator,"my_ridge.pkl")
# 加载模型
estimator = joblib.load("my_ridge.pkl")
3.6 无监督学习K-means
kmeans性能评估指标:bi其实就是相当于每个簇的内部距离,ai就是相当于不同簇之间的距离,也就是外部距离,如果bi>>ai的话,轮廓系数就等于1,这种情况是我们希望看到的,如果ai>>bi的话,轮廓系数就等于-1,这种情况是我们不希望看到的。


api:参数为特征值和得到的聚类结果
![]()
k-means特点:缺点是随机取聚类中心的时候可能取的中心取到了一起,可能就会导致结果局部最优,解决方法是进行多次聚类,多取几次聚类中心进行聚类。