【前沿技术】扩散模型是什么
0. 前言
扩散模型的灵感来自非平衡热力学。他们定义了一个马尔可夫扩散步骤链，以缓慢地将随机噪声添加到数据中，然后学习逆转扩散过程以从噪声中构建所需的数据样本。与VAE或流动模型不同，扩散模型是通过固定程序学习的，并且潜在变量具有高维数（与原始数据相同）。
图一. 不同类型的生成模型概述
1. 前向扩散过程
给定一个从真实数据分布
中采样的点，让我们定义一个前向扩散过程，在这个过程中，我们分
步向样本中添加少量的高斯噪声，产生一系列噪声样本
。步长由方差表
表示。
随着步长t变大，数据样本
会逐渐失去其可区分的特征。最终，当
时
等价于各向同性高斯分布。
图 2.通过缓慢添加（去除）噪声来生成样本的正向（反向）扩散过程的马尔可夫链。（图片来源：Ho et al. 2020）
上述过程的一个很好的特性是，我们可以使用重新参数化技巧以封闭形式在任何任意时间步t长进行采样 
。让
和
:
(*)回想一下，当我们合并两个具有不同方差的高斯分布时，
和
，新分布是
。这里合并的标准差是
。
通常，当样本变得更嘈杂时，我们可以承受更大的更新步骤，因此 
,
。
2. 逆向扩散过程
如果我们能反转上述过程并从中
采样，我们能够从高斯噪声输入中重建真实样本。
请注意，如果
足够小，
也将是高斯的。不幸的是，我们不能轻易估计，因为它需要使用整个数据集，因此我们需要学习一个模型
来近似这些条件概率，以便运行反向扩散过程。
在数学中，闭式表达式是使用有限数量的标准运算的数学表达式。这可能包括常量、变量、某些众所周知的运算（例如 + − × ÷）和函数（例如 n 次方根、指数、对数、三角函数、反双曲函数），但通常不包括极限或积分。
3. 扩散模型的训练
- 正向扩散→在图像中添加噪声。
- 反向扩散过程→去除图像中的噪声。
前向扩散过程逐步将高斯噪声添加到输入图像中。尽管如此，使用以下封闭式公式可以更快地完成，以直接获取特定时间步长 t 的噪声图像：
反向扩散过程不可直接计算，我们训练神经网络
来逼近它。
训练目标损失函数如下：
![L_{simple}=E_{t,x_{0},\varepsilon}[||\mathbf{\varepsilon-\varepsilon_{\theta}(x_{t,t})}||^{2}]](http://img.e-com-net.com/image/info8/1ff3dd2060134eb7ba959ba8f4d532d2.png){kind=small}
Training 训练
在每一轮训练中：
1.将为每个训练样本(图像)选择一个随机的时间步长t。
2.将高斯噪声(对应于t)应用于每个图像。
3.将时间步长转换为嵌入(向量)。
每一个训练步骤：
Sampling(采样)
采样是指从高斯噪声中绘制图像。下图显示了如何使用经过训练的 U-Net 来生成图像：
Diffusion Speed Problem (扩散速度问题)
如您所见，扩散（采样）过程迭代地将全尺寸图像馈送到 U-Net 以获得最终结果。这使得纯扩散模型在总扩散步数 T 和图像尺寸较大时非常慢。
因此，Stable Diffusion 旨在解决这个问题。
Stable Diffusion(稳定扩散)
稳定扩散的原名是“潜在扩散模型”（LDM）。顾名思义，扩散过程发生在潜在空间中。这就是它比纯扩散模型更快的原因。
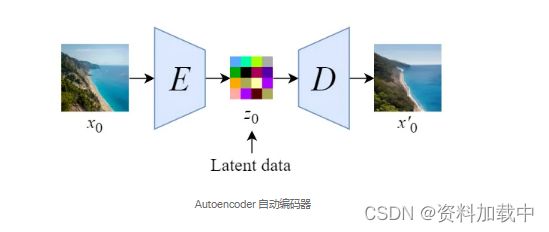
Departure to Latent Space
我们将首先训练一个自动编码器来学习将图像数据压缩为低维表示。
- 通过使用经过训练的编码器 E，我们可以将全尺寸图像编码为低维潜在数据（压缩数据）。
- 通过使用经过训练的解码器 D，我们可以将潜在数据解码回图像。
Latent Diffusion (潜伏扩散)
将图像编码为潜在数据后，将在潜在空间中完成前向和反向扩散过程。
前向扩散过程→向添加噪声。
反向扩散过程→去除中的噪声。
Conditioning(条件嵌入)
Stable Diffusion 模型的真正强大之处在于它可以从文本提示生成图像。这是通过修改内部扩散模型以接受条件输入来完成的。
通过交叉注意力机制增强其去噪U-Net，将内扩散模型转变为条件图像生成器。
上图中的开关用于控制不同类型的调节输入：
对于文本输入，首先使用语言模型τθ（例如BERT，CLIP）将它们转换为嵌入（向量），然后通过（多头）注意力（Q，K，V）层将它们映射到U-Net中。
对于其他空间对齐的输入（例如语义图、图像、修复），可以使用串联来完成调节。
Training(训练)
训练目标（损失函数）与纯扩散模型中的目标非常相似。唯一的变化是：
- 输入潜在数据
而不是图像 
。 - 向 U-Net 添加了调节输入
。
Sampling(采样)
由于潜在数据的大小比原始图像小得多，因此去噪过程会快得多。
Architecture Comparison(架构比较)
Pure Diffusion Model(纯扩散模型)
Stable Diffusion (Latent Diffusion Model)
稳定扩散（潜伏扩散模型）
总结：
- 扩散模型分为正向扩散和反向扩散两部分。
- 正扩散可以用封闭形式的公式计算。
- 反向扩散可以用训练好的神经网络来完成。
- 为了近似所需的去噪步骤q，我们只需要使用神经网络εθ近似噪声εₜ。
- 在简化损失函数上进行训练可以获得更好的样本质量。
- 稳定扩散(潜扩散模型)是在潜空间中进行扩散过程，因此比纯扩散模型快得多。
参考链接：
Diffusion 和Stable Diffusion的数学和工作原理详细解释 - 知乎
https://medium.com/@steinsfu/stable-diffusion-clearly-explained-ed008044e07e