What Do They Capture? - A Structural Analysis of Pre-Trained Language Models for Source Code
A Structural Analysis of Pre-Trained Language Models for Source Code
-
- 1 Introduction
- 2 Motivation
- 3 Structural Analysis of Pre-Trained Language Models for Source Code
-
- 3.1 Attention Analysis
- 3.2 Structural Probing on Word Embedding
- 4.3 Syntax Tree Induction
Comments: Accepted by ICSE 2022 (The 44th International Conference on Software Engineering)
Subjects: Software Engineering (cs.SE); Artificial Intelligence (cs.AI)
Cite as: arXiv:2202.06840 [cs.SE]
(or arXiv:2202.06840v1 [cs.SE] for this version)
https://doi.org/10.48550/arXiv.2202.06840
1 Introduction
代码表示学习(也称 code embedding)旨在将源代码的语义编码为分布式向量,在最近基于深度学习的代码智能模型中起着重要作用。
当前的 code embedding 方法主要分为两类,有监督和无监督(self-supervised)学习。
- 有监督方法通常是为遵循 encoder-decoder 体系结构的特定任务而开发的。在这个体系结构中,encoder 网络永续生成程序的向量表示,然后将这个向量作为输入馈送到 decoder 网络中,以执行一些预测任务,例如摘要生成或者 token 序列预测。
- 为软件工程任务开发大规模代码语料库上的预训练模型。
存在问题:
- 在 NLP 领域,最近有一些研究从注意力分析和任务探测的角度来解释预训练的语言模型,如BERT,重点研究 BERT 的内在机制。但是在软件工程中并没有这种工作。
- 我们看到预训练的语言模型在各种软件工程任务中实现了卓越的性能,但不理解它们为什么工作。
- 目前的一些工作研究只表明了代码嵌入技术在哪些场景下效果更好,而没有解释嵌入为什么会取得良好效果的内在机制。在软件工程任务的上下文中,我们仍然不清楚为什么预训练的语言模型会起作用,以及它们实际上捕获了什么。
**主要贡献:**探讨预训练代码模型的可解释性。现有的预训练语言模型能否学习源代码的语法结构?
- 分析自注意力权重(self-attention weights),并将权重与语法结构对齐。给定一个代码片段,我们的假设是,如果两个 token 在AST中彼此接近,即具有邻域关系,则分配给它们的关注权重应该很高。我们的分析表明,attention 可以捕捉源代码的高级结构属性,即 AST 中的基序结构。
- 设计了一种结构探测方法,以研究语法结构是否嵌入到了 预训练模型的线性变换的上下文词嵌入中。
- 研究了源代码的预训练语言模型是否能够在没有训练的情况下生成语法树。
2 Motivation
在NLP领域已有研究指出,Transformer 中的自注意机制具有捕获自然语言中特定语法信息的能力。受此启发,我们设想并研究一个代码片段的预训练模型的注意力分布。下图显示了带有AST的 Python代码片段。 本文中,将AST的语法结构定义为 一个 motif-structure,该语法结构由一个非叶子节点及其子节点(例如,if_statement 和 block)组成。我们认为代码的语法信息可以通过一系列 motif structures 组成。
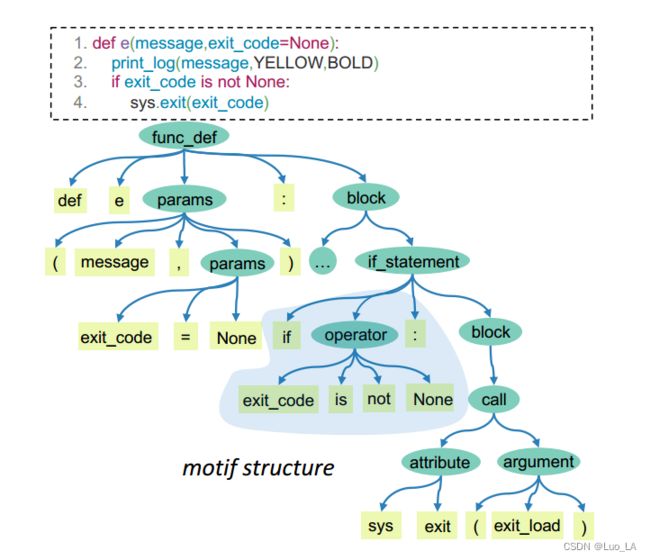
给定一个代码片及其相应的AST,下图可视化了特定层(例如第5层)的自注意力热图,是多头的注意力权重的平均值。在下图中,我们可以观察到,自注意热图中存在几种模式。用红色标记的矩形。这些矩形表示 code tokens 来自一个组。我们发现每一组 tokens 在 AST中是彼此接近的。以 “ if exit_code is not None” 为例, 这是一个 if 语句,我们可以发现,在AST中所有这些 token 都是在 if_statement 的同一个分支中。另外,这些 code tokens 在 自注意热图中也紧密相连。

我们还可视化了特定头部(第五层的 第12 个头)中的自注意分布,并分析两个 token 之间的连接关系。如下图所示。线的亮度表示特定头部的注意力权重。如果连接的节点出现在相应的 AST 的 motif structure 结构中,我们用红色标记这些线。从图中,我们可以看到,在一个motif struture 结构中的 code tokens (如 if exit_code not None)确实被突出显示为 自注意力上的 紧密连接。
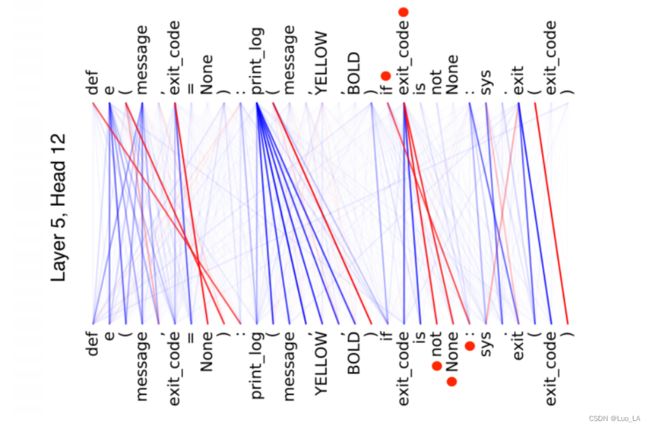
在上述观察的推动下,本文通过分析自注意机制,研究了为什么预训练的源代码语言模型有效,以及它们捕获了哪些特征相关性。特别地,我们在Transformer框架下分析了自注意机制的两个输出,即注意力分布和生成的隐藏向量。
3 Structural Analysis of Pre-Trained Language Models for Source Code
( w 1 , w 2 , . . . , w n ) (w_1,w_2,...,w_n) (w1,w2,...,wn) 表示代码片段 c c c 的 code token 序列,长度为 n n n 。在第 l l l 层 transformer ,使用 h 1 l , h 2 l , . . . , h n l h_1^l,h_2^l,...,h_n^l h1l,h2l,...,hnl 来表示每个 code token 的上下文表示序列。
3.1 Attention Analysis
首先分析 自注意权重,这是基于 transformer 的预训练模型的核心机制。直观的说,注意力定义了 每一对 code tokens 的紧密程度。
从注意力分析的角度,我们的目标是分析 注意力是如何与源代码中的语法关系保持一致的。我们考虑语法关系使得共享同一个父节点的两个AST tokens之间的注意力权重很高。下图,给定一个带有 AST的代码片段,我们可以看到叶节点 for 和 in 共享父节点,如预期的一样,该结构与两节点之间的注意力权重 α f o r , i n \alpha_{for,in} αfor,in 是相对应的。
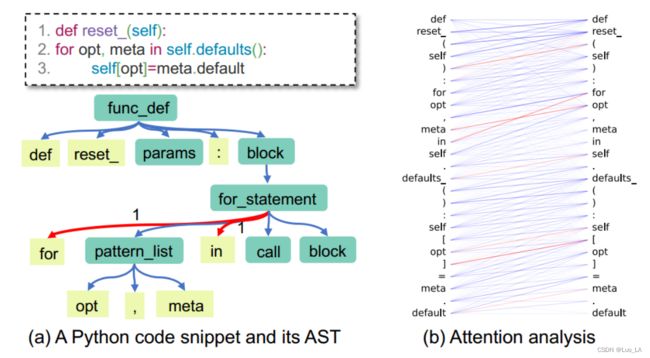
具体来说,在每一个 Transformer 层上,我们可以获得一组输入的 注意力权重 α \alpha α ,其中 α i , j > 0 \alpha_{i,j}>0 αi,j>0 是 第 i i i 个 code token 和 第 j j j 个 code token 之间的注意力权重。在这里定义一个指示函数 f ( w i , w j ) f(w_i,w_j) f(wi,wj) ,如果 w i w_i wi 和 w j w_j wj 存在语法关系( w i w_i wi 和 w j w_j wj 在AST 中拥有相同的父节点)函数返回值为1,否则为0。我们将 w i w_i wi 和 w j w_j wj 之间的注意力权重定义为 α i , j ( c ) \alpha_{i,j}(c) αi,j(c) ,如果 w i w_i wi 和 w j w_j wj 非常接近,那么注意力权重就应该大于一个阈值,即 α i , j ( c ) > θ \alpha_{i,j}(c)>\theta αi,j(c)>θ 。 因此,聚合在一个数据集 C C C 上的高注意力分数的 token pairs 的比例可以定义如下:
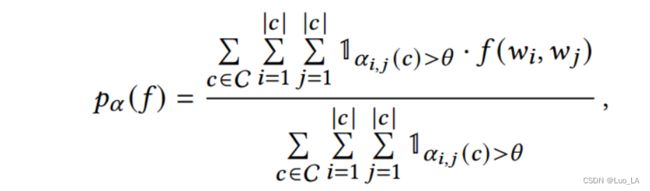
其中 θ \theta θ 是高置信度注意力权重的阈值。
由上式可以看出,注意力对齐部分只依赖于注意力权重 α i , j ( c ) \alpha_{i,j}(c) αi,j(c) 的绝对值。我们假设那些关注位置的头部,即那些专注于前一个或下一个code token 的头部,不会与代码的语法结构很好地对齐,因为它们不考虑代码标记的内容。为了区分头部是否关注 code token 的内容或位置,我们进一步研究了注意力可变性,它测量了注意力在不同输入下的变化。注意力可变性的正式定义如下:
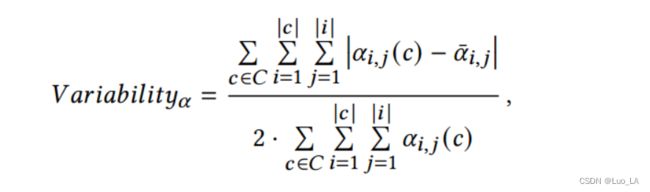
其中 α ˉ i , j \bar{\alpha}_{i,j} αˉi,j 是 所有 c ∈ C c \in C c∈C 上 α ˉ i , j ( c ) \bar{\alpha}_{i,j}(c) αˉi,j(c) 的平均值。对于每一 c ∈ C c \in C c∈C ,我们只包含前 N 个 tokens (N = 10)为了确保 在每个位置 i 由足够的数据。整个序列的位置模式几乎是一致的。高可变性表明是依赖内容的头部,而低可变性表明是不依赖内容的头部。
3.2 Structural Probing on Word Embedding
提出一种结构探测分析方法来研究预训练模型是否在其上下文词嵌入中嵌入句法结构。方法的关键思想是,如果变换空间有 两个词向量之间的欧几里得距离和语法树中词之间的边数是相对应的 性质,则树结构是嵌入的。
那么为什么语法树节点之间的距离对语法信息很重要呢?这是因为距离度量(即每对词之间的路径长度)可以简单的通过判断节点 u , v u, v u,v 之间距离是否为1来确定 u , v u,v u,v 是否为邻居节点,从而恢复语法树。
下图给出了一个简单的例子来说明距离和语法结构之间的联系。 ( w 1 , . . . , w i , . . . , w j , . . . , w n ) (w_1,...,w_i,...,w_j,...,w_n) (w1,...,wi,...,wj,...,wn) 表示代码片段 c c c 的 code tokens 序列。如果我们知道每对节点之间的距离,我们可以归纳出代码的语法结构。注意,距离度量(度量任意两个代码标记之间的距离)可以在一定程度上了解代码的全局语法结构。
以与父节点相同的叶节点(上图中的 for 和 in )为例,这两个节点之间距离的欧氏平方为2。我们首先通过线性变换 B 将这两个标记的表示映射到一个隐藏空间中,得到向量 V e c t o r f o r Vector_{for} Vectorfor 和 V e c t o r i n Vector_{in} Vectorin ,我们认为,如果 V e c t o r f o r Vector_{for} Vectorfor 和 V e c t o r i n Vector_{in} Vectorin 之间的欧氏距离的平方接近于2,那么for和in之间的语法结构被很好地保留了下来。
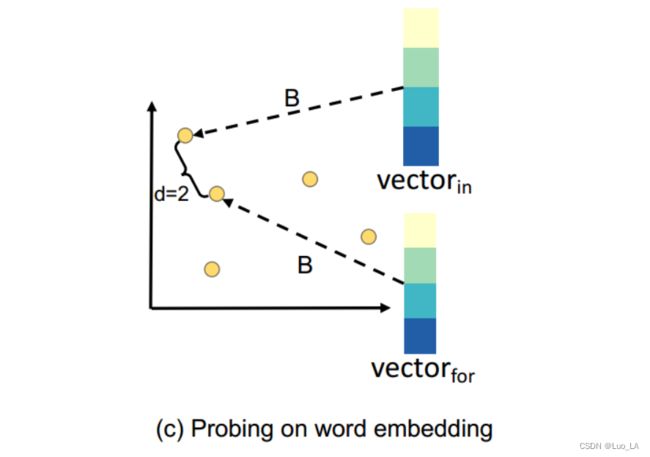
特别地,我们以监督的方式学习了映射函数。正式地,给定一个代码序列 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn 作为输入,每个模型层生成词向量 h 1 , h 2 , . . . , h n h_1,h_2,...,h_n h1,h2,...,hn 。我们计算高维隐藏空间中两个词向量 h i h_i hi 和 h j h_j hj 之间距离的平方如下:
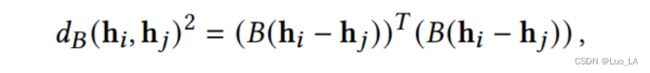
其中 i i i 和 j j j 是代码序列中 单词的索引。我们使用的结构探测的参数正是矩阵 B (线性映射),它被训练用来重建源代码训练集中代码序列 中所有词对 ( w i , w j ) (w_i,w_j) (wi,wj) 之间的树距离。我们将参数训练的损失函数定义为:
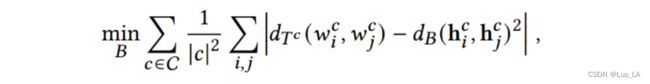
其中 ∣ c ∣ |c| ∣c∣ 是代码序列 c c c 的长度。 d T c ( w i c , w j c ) d_{Tc}(w_i^c,w_j^c) dTc(wic,wjc) 表示的是 AST 中 code tokens 之间的距离, d B ( h i c , h j c ) 2 d_{B}(h_i^c,h_j^c)^2 dB(hic,hjc)2 表示对于代码序列 c c c ,code tokens 的嵌入向量之间的距离。第一个求和计算所有训练序列的平均距离,而第二个求和计算代码序列中任意两个单词的所有可能组合。这种监督训练的目标是向后传播误差并更新线性映射矩阵的参数 B。
4.3 Syntax Tree Induction
我们提出在不进行训练的情况下,研究预训练代码模型的归纳语法结构能力。
这个方法的关键是,如果两个令牌之间的距离很近(如,具有相似的注意力分布,或具有相似的表示),则它们在语法树中应该很近,即共享相同的父节点。
基于这一观点,我们提出从两个 token 之间的距离来推导出语法树。我们假设,如果从预训练模型中得到的推导树与标准语法树相似,我们可以合理地推断在模型预训练过程中保留了语法结构。
给定代码序列 ( w 1 , w 2 , . . . , w n ) (w_1,w_2,...,w_n) (w1,w2,...,wn),我们计算得到 d = ( d 1 , d 2 , . . . , d n − 1 ) d=(d_1,d_2,...,d_{n-1}) d=(d1,d2,...,dn−1),其中 d i d_i di 对应于 token w i w_i wi 和 w i + 1 w_{i+1} wi+1 之间的语法距离。 d i d_i di 如下定义:
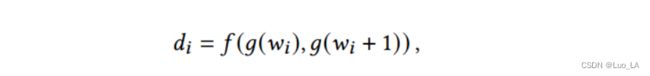
其中 f ( . , . ) f(.,.) f(.,.) 表示距离测量函数, g ( . ) g(.) g(.) 表示代码表示学习函数。
我们使用不同的距离测量函数,从中间表示向量和自注意分布 测量两个 token 之间的语法距离。
令 g l v g_l^v glv 和 g l , k d g_{l,k}^d gl,kd 表示在 第 l l l 层的 第 k k k 个头部的 中间表示和自注意函数。为了计算向量之间的相似性,我们有很多选择,包括中间表示和注意力分布。例如,我们可以使用 1 和 2 来计算两个中间表示向量之间的相似性。我们可以使用Jensen-Shannon散度和Hellinger距离来计算两个注意力分布之间的相似度。表1总结了所有可用的距离测量函数。

一旦计算出距离向量d,我们就可以通过基于输入递归划分的简单贪婪自顶向下推理算法轻松地将其转换为目标语法树,如算法1所示。或者,这个树的重建过程也可以用自下而上的方式来完成,这有待于进一步的探索。
给语法距离注入偏差。从我们的观察来看,源代码的AST倾向于向右倾斜。因此,我们需要对推理树施加一些影响,使它们可以按照标准 AST 的性质适度向右倾斜。为实现这一目标,我们提出通过简单地修改句法距离的值来将归纳偏差注入框架。特别地,我们引入了右偏性偏差来影响生成树,使其适当地右偏。通过将下面的线性偏差加入 d i ^ \hat{d_i} di^ 来计算 :
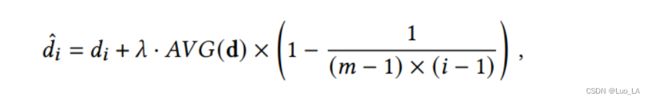
其中 A V G ( . ) AVG(.) AVG(.) 输入向量中所有元素的平均值。 i i i 从 1 到 m m m , m = n − 1 m=n-1 m=n−1
两棵树之间的相似性。介绍 计算 推理树和标准 AST 之间相似性的方法。
首先,将树结构转换为中间节点的集合,其中每个中各节点有两个叶节点组成。然后测量两个集合之间的相似性。下图为一个简单的示例。

标准 AST 由四个中间节点组成。对于每个中间节点,使用两个叶节点来进一步展开它。同样将推理树转化为叶节点的 集合。
给定两组集合,我们使用 F 1 F_1 F1 分数来测量他们的相似性。令 S S S 表示为 标准树的集合, S ′ S' S′ 表示预测树的集合,我们可以通过 p r e c i s i o n = S ∩ S ′ S ′ , r e c a l l = S ∩ S ′ S precision=\frac{S∩S'}{S'},recall=\frac{S∩S'}{S} precision=S′S∩S′,recall=SS∩S′ 分别计算准确率和召回率, F 1 F_1 F1 分数 是准确率和召回率的调和平均值。
