抽签问题_二分查找算法

 

问题描述：

你的朋友提议玩一个游戏：将写有数字的n个纸片放入口袋中，你可以从口袋中抽取4次纸片，每次记下纸片上的数字后都将其放回口袋中。如果这4个数字的和是m，就是你赢，否则就是你的朋友赢。你挑战了好几回，结果一次也没赢过，于是怒而撕破口袋，取出所有纸片，检查自己是否真的有赢的可能性。请你编写一个程序，判断当纸片上所写的数字是k,k，…, kn时，是否存在抽取4次和为m的方案。如果存在，输出 Yes;否则，输出No。

其中限制条件为：l ≤n≤1000 ； 1 ≤m≤10^8 ； 1 ≤k≤10^8

问题分析：

遍历抽出四张卡片的所有可能情况，判断总和是否为m，通过结果从而对应相应输出。

（一）暴力解法

主代码段如下：

for(int a=0;a

可见，本问题可以使用循环嵌套方式来解决，但是问题真正被解决的前提是要确保问题解决的有效性，当n的值很大时，这种方法便会浪费很多时间，其时间复杂度为O(n^4)，当n=1000时，其时间复杂度为10^12，过大。

现在面临的问题是：如何改进算法，降低时间复杂度。

解决办法：

代码段中的第四层循环主要是用来判断抽取出的四张卡片总和，全部遍历所耗时间过长，这时引入二分查找算法来解决此问题，那么什么是二分查找？

二分查找：二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。注：摘自百度百科。

根据二分查找的定义，可以了解到要优化此问题的查找效率，前提是将问题涉及到的线性表进行顺序排列存储，利用sort函数进行排列是必不可少的；其次通过深入学习可以很容易了解到，二分查找的重点在于“确定”二字，确定目标值，确定左边界，确定右边界。

（二）二分查找替换第四层循环

根据上面的分析，我们需要在编程之前确定三个值：目标值、左边界、右边界。

其中第四层的判断条件为k[a]+k[b]+k[c]+k[d]==m,转换思路，即为找出k[d]，k[d]必须满足k[d]=m-(k[a]+k[b]+k[c])，因此目标值已确定，即为m-(k[a]+k[b]+k[c])。

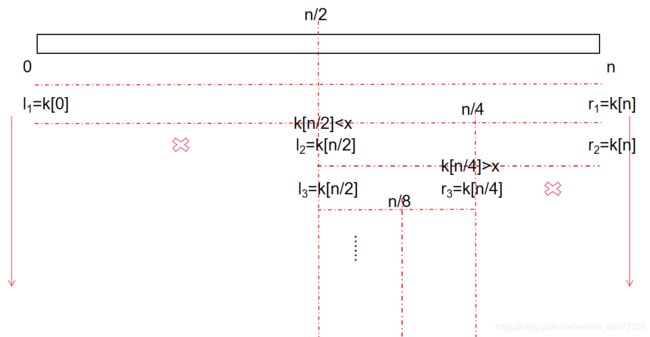
再来分析左边界和右边界，可以得知，线性表中间值>目标值，则目标值位于线性表中间值以下，反之在线性表中间值以上，其中也存在目标值等于中间值的情况，对本问题而言，可以直接得到对比结果。

主代码段如下：

bool binary_search(int x){    //x为目标值
    int l=0,r=n;
    while(r-1>=1){
        int i=(l+r)/2;
        if(k[i]==x)  return true;
        else if(k[i]

 通过二分法替代第四层循环，可以得到此种方法时间复杂度为O(n^3*logn)，很大程度上降低了此问题的时间复杂度，但是对于n很大的情况，也难以达到我们所期望的效率，这时我们就要思考第四层的替换方式能否应用在第三层循环中，答案是肯定的。

（三）二分查找替代第三层和第四层循环

保持原来的思维方式，找出二分查找最主要的三个值：目标值、左边界、右边界，其中目标值很好确定，即为m-(k[a]+k[b])，但是边界该如何确定呢？

这时我们必须要想到，当目标值改变了，所对应查找的线性表也必须要随之更新，此次我们要替换的是第三层和第四层循环，那线性表对应的值也应该是能够替代第三和第四层循环的数值，这样分析下来，我们可以很容易发现，目标值所在线性表里面的数由n个变为n*n个，在进行线性表操作之前，确定正确的线性表值是整个程序正确合理运行的基础。

好了，我们已经得到了新的线性表，得到了新的目标值，还请记得二分搜索的前提！！！sort函数又一次派上了用场。接下来的分析方式和上面并无区别，主代码段如下：

bool binary_search(int x){    //x为目标值
    int l=0,r=n;
    while(r-1>=1){
        int i=(l+r)/2;
        if(kk[i]==x)  return true;
        else if(kk[i]

根据上面代码可以知道，替换第三和第四层循环嵌套又一次减低了代码的时间复杂度，降为O(n^2*logn)。

到这里，二分搜索的简单应用已经完成，可能会有人想，既然可以替换第四层以及替换第三层，那么为何不继续替换下去，替换第二层和第一层岂不是更优？没错，我当时就是这样想的，但是其实并非如此，当我们使用二分法进行搜索时，其搜索对应线性表的形成也是需要循环遍历的，要知道一旦有循环，便会耗时，本文最初求解时程序中有四层循环嵌套，利用二分搜索算法后，优化为两层，更深入来讲优化后的时间复杂度为:O(n^2*logn)+O(n^2*logn)，其中包含了排序时间和循环时间，若继续替换第二层，会导致排序时间复杂度上升为三次，循环时间复杂度下降为一次，但总体时间复杂度是升高的，和木桶定律有些许相似。

注：借鉴了《挑战程序设计竞赛》。