MATLAB中插值拟合曲线

编译环境：MATLAB 2018a win64；

2. 确定地球与金星之间的距离
天文学家在1914年8月份的7次观测中，测得地球与金星之间距离（单位：米），并取其常用对数值，与日期的一组历史数据如下表：

日期（号）	18	20	22	24	26	28	30
距离对数	9.9617724	9.9543645	9.9468069	9.9390950	9.9312245	9.9231915	9.9149925

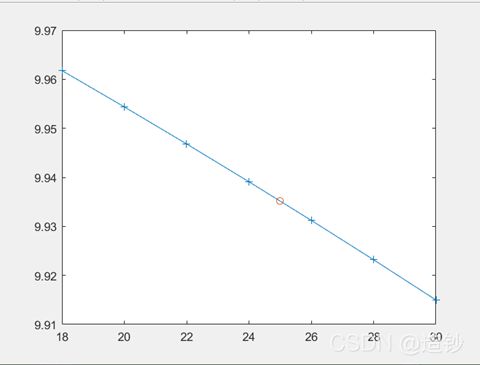
由此推断何时金星与地球的距离（米）的对数值为9.9351799？

解：代码如下所示

clc;
x=[18,20,22,24,26,28,30];
y=[9.9617724,9.9543645,9.9468069,9.9390950,9.9312245,9.9231915,9.9149925];
y1=9.9351799;
z=interp1(y,x,y1,'linear');
xlabel('x');
ylabel('y');
plot(x,y,'-+',z,y1,'o');
disp(['插入9.9351799所在点的z值为',int2str(z)]);

结果如图所示。

 

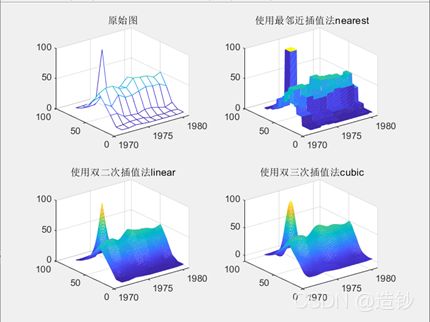
气旋分布的可视化
下面是南半球不同年份在七月份按不同纬度的气旋数据，用二维插值，试

可视化其气旋分布，并对比最近邻插值、双二次插值、双三次插值。

	1972	1973	1974	1975	1976	1977	1978	1979	1980	1981
0-10	0	0	2	1	0	0	0	0	0	1
10-20	0	1	3	3	3	0	1	0	2	1
20-30	15	15	7	6	5	9	9	6	3	8
30-40	29	22	38	31	31	35	39	37	37	31
40-50	42	48	48	41	39	52	50	49	44	49
50-60	25	29	30	31	37	49	38	43	41	28
60-70	12	20	21	15	14	19	23	30	27	21
70-80	4	3	4	92	7	6	2	2	8	8
80-90	0	0	1	0	0	0	0	0	0	0

解：代码如下所示；

x=[1972:1981];
y=[10:10:90];
z=[0,0,2,1,0,0,0,0,0,1
    0,1,3,3,3,0,1,0,2,1
    15,15,7,6,5,9,9,6,3,8
    29,22,38,31,31,35,39,37,37,31
    42,48,48,41,39,52,50,49,44,49
    25,29,30,31,37,49,38,43,41,28
    12,20,21,15,14,19,23,30,27,21
    4,3,4,92,7,6,2,2,8,8
    0,0,1,0,0,0,0,0,0,0];
mesh(x,y,z);
xi=linspace(1972,1981,100);
yi=linspace(10,90,100);
[xii,yii]=meshgrid(xi,yi);
subplot(2,2,1);
mesh(x,y,z);
title('原始图')
subplot(2,2,2);
Z1=interp2(x,y,z,xii,yii,'nearest');
mesh(xii,yii,Z1);
title('使用最邻近插值法nearest')
subplot(2,2,3);
Z1=interp2(x,y,z,xii,yii,'linear');
mesh(xii,yii,Z1);
title('使用双二次插值法linear')
subplot(2,2,4);
Z1=interp2(x,y,z,xii,yii,'cubic');
mesh(xii,yii,Z1);
zlim([-10,100])
title('使用双三次插值法cubic')

结果下图所示：

 

考察温度x对产量y的影响，测得下列10组数据：

 用拟合算法，求y关于x的多项式方程并绘图。

 解：代码如下所示：

format rat;
wendu=[20:5:65];
chanliang=[13.2,15.1,16.4,17.1,17.9,18.7,19.6,21.2,22.5,24.3];
duoxiangshi=polyfit(wendu,chanliang,5);
B=polyval(duoxiangshi,wendu);
plot(wendu,chanliang,'rx',wendu,B,'-b');
legend('实际值','5次拟合预测曲线');
disp(poly2str([duoxiangshi],'x'));

拟合曲线结果为：4.1026e-09x^5-6.1166e-06x^4+0.0011301x^3-0.077339x^2+2.4234x-12.4173

 

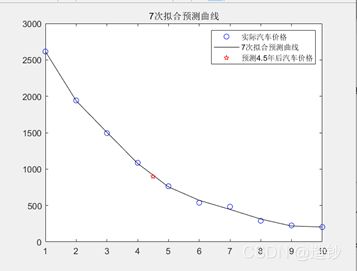
旧车价格预测
    某年美国旧车价格的调查资料如下表，其中xi表示轿车的使用年数，yi表示相应的平均价格。试分析用什么形式的曲线来拟合上述的数据，并预测使用4.5年后轿车的平均价格大致为多少？

xi	1	2	3	4	5	6	7	8	9	10
yi	2615	1943	1494	1087	765	538	484	290	226	204

解：代码如下所示：

x=[1:10];
y=[2615,1943,1494,1087,765,538,484,290,226,204];
A=polyfit(x,y,7);
B=polyval(A,x);
fx=poly2str([A],'x');
disp(fx);
z=polyval(A,4.5);
plot(x,y,'ob',x,B,'-k',4.5,z,'rp');
title('7次拟合预测曲线')
legend('实际汽车价格','7次拟合预测曲线','预测4.5年后汽车价格');
disp(['预测4.5年后汽车价格为：',int2str(z)]);

预测函数为：

-0.037967x^7+1.5617x^6-26.0571x^5+226.0931x^4-1088.7609x^3+ 2913.676 x^2 - 4473.995 x + 5063.2

预测4.5年后汽车价格为：898

拟合曲线为：