线性调频(LFM信号)脉冲压缩雷达matlab仿真- 脉冲压缩 测距 测速 距离速度三维像(附matlab代码)
**阅读须知:**本文摘取自AIMZZY原创文章,并做改动,在此致谢
原文链接:https://blog.csdn.net/AIMZZY/article/details/106467080
线性调频脉冲压缩雷达仿真
- 1.线性调频脉冲雷达的工作原理
- 2.线性调频信号(LFM信号)
-
- 2.1.LFM信号(时域分析)
-
- 2.1.1.LFM信号模型
- 2.1.2.LFM信号时域仿真
- 2.2.LFM信号(频域分析)
-
- 2.2.1.驻定相位原理(POSP)
- 2.2.2.LFM信号频谱仿真
- 3.脉冲压缩技术
-
- 3.1.匹配滤波器
-
- 3.1.1.匹配滤波器的推导
- 3.1.2.匹配滤波器的理解
- 3.2.LFM信号脉冲压缩的匹配滤波器实现
-
- 3.2.1.时域匹配滤波
- 3.2.2.频域匹配滤波
-
- 3.2.2.1.方法一
- 3.2.2.2.方法二
- 3.2.2.3.方法三
- 3.3.LFM脉冲压缩加窗处理
-
- 3.3.1.性能指标
- 3.3.2.各类窗的对比
- 3.3.3.脉冲压缩加窗
-
- 3.3.3.1.Hanning窗脉冲压缩加窗举例
- 3.3.3.2.Blackman窗脉冲压缩加窗举例
- 4.LFM脉冲压缩雷达测距
-
- 4.1.测距雷达的任务要求:
- 4.2.系统模型的构建
- 4.3.关于距离分辨率
- 4.4.最终效果呈现
- 4.5.LFM脉冲压缩雷达测距matlab代码
- 5.脉冲多普勒雷达同时实现测距测速
-
- 5.1.任务介绍
- 5.2.matlab代码
- 5.2.测距测速结果展示
- 5.2.1.情况(1)
- 5.2.2.其他情况
- 6.脉冲多普勒雷达距离速度三维像
-
- 6.1.结合第五部分实现三维信息表示:
- 6.2.matlab代码实现
1.线性调频脉冲雷达的工作原理
2.线性调频信号(LFM信号)
2.1.LFM信号(时域分析)
2.1.1.LFM信号模型
2.1.2.LFM信号时域仿真
%%线性调频信号
T=10e-6; %p脉冲持续时间10us
B=30e6; %线性调频信号的频带宽度30MHz
K=B/T; %调频斜率
Fs=2*B;Ts=1/Fs; %采样频率和采样间隔
N=T/Ts;
t=linspace(-T/2,T/2,N);
St=exp(j*pi*K*t.^2); %线性调频信号
subplot(211)
plot(t*1e6,real(St));
xlabel('时间/us');
title('线性调频信号的实部');
grid on;axis tight;
subplot(212)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St))));
xlabel('频率/MHz');
title('线性调频信号的幅频特性');
grid on;axis tight;
(1)信号参数
① 时宽 Tr = 1 us
② 带宽 Br = 100 MHz
③ 采样率 Fs = 4 * Br
(2)仿真结果
| 信号实部 | 信号虚部 | 信号频率 | column4 |
|---|---|---|---|
 |
 |
 |
 |
%% 线性调频与脉冲压缩
clear,clc,close all
set(0,'defaultfigurecolor','w')
%% Chirp信号参数设置
Tr = 1e-6;%时宽
Br = 200e6;%带宽
Fs = 4*Br;%采样率
%% Chirp信号参数导出
Kr = Br/Tr;%调频率
N = round( Tr / (1/Fs) );%采样点数
t = linspace( -Tr/2 , Tr/2 , N);%在[-Tp/2,Tp/2]选取采样点
%% Chirp信号生成
st = ( abs(t) < Tr/2 ) .* exp( 1j * pi * Kr * t.^2 );
f_chirp= Kr * t; %信号频率
phase_chirp = pi * Kr * t.^2;%信号相位
% 时域
figure,plot( t*1e6, real(st) ),xlabel('t /us'),ylabel('幅度'),title('Chirp信号实部');
figure,plot( t*1e6, imag(st) ),xlabel('t /us'),ylabel('幅度'),title('Chirp信号虚部');
figure,plot( t*1e6, f_chirp/1e6 ),xlabel('t /us'),ylabel('频率 /MHz'),title('Chirp信号频率');
figure,plot( t*1e6, phase_chirp ),xlabel('t /us'),ylabel('相位 /rad'),title('Chirp信号相位');
2.2.LFM信号(频域分析)
2.2.1.驻定相位原理(POSP)
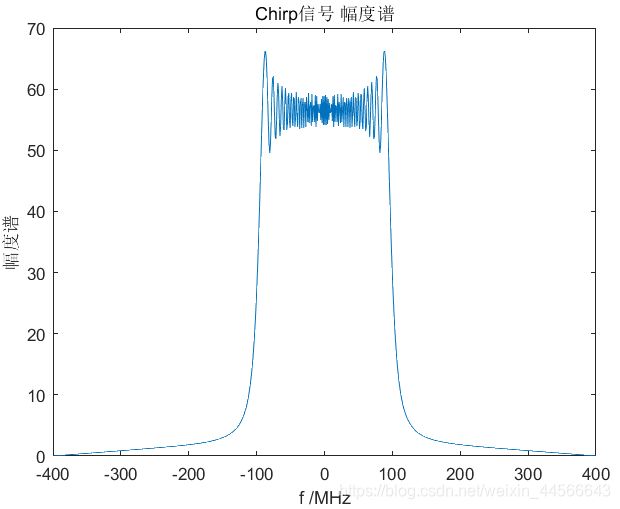
2.2.2.LFM信号频谱仿真
| 频谱幅度谱 | 频谱相位谱 |
|---|---|
 |
 |
%% 线性调频与脉冲压缩
clear,clc,close all
set(0,'defaultfigurecolor','w')
%% Chirp信号参数设置
Tr = 1e-6;%时宽
Br = 200e6;%带宽
Fs = 4*Br;%采样率
%% Chirp信号参数导出
Kr = Br/Tr;%调频率
N = round( Tr / (1/Fs) );%采样点数
t = linspace( -Tr/2 , Tr/2 , N);%在[-Tp/2,Tp/2]选取采样点
%% Chirp信号生成
st = ( abs(t) < Tr/2 ) .* exp( 1j * pi * Kr * t.^2 );
f_chirp= Kr * t; %信号频率
phase_chirp = pi * Kr * t.^2;%信号相位
%% 频谱
freq = linspace(-Fs/2,Fs/2,N);%频域采样
Sf = fftshift( fft(st) );
% 频域
figure,plot( freq/1e6,abs(Sf) ),xlabel('f /MHz'),ylabel('幅度谱'),title('Chirp信号 幅度谱');
figure,plot( freq/1e6,-pi*freq.^2/Kr ),xlabel('f /MHz'),ylabel('相位谱'),title('Chirp信号 相位谱');
3.脉冲压缩技术
3.1.匹配滤波器
3.1.1.匹配滤波器的推导
3.1.2.匹配滤波器的理解
3.2.LFM信号脉冲压缩的匹配滤波器实现
3.2.1.时域匹配滤波
%% 线性调频与脉冲压缩
clear,clc,close all
set(0,'defaultfigurecolor','w')
%% Chirp信号参数设置
Tr = 1e-6;%时宽
Br = 200e6;%带宽
Fs = 4*Br;%采样率
%% Chirp信号参数导出
Kr = Br/Tr;%调频率
N = round( Tr / (1/Fs) );%采样点数
t = linspace( -Tr/2 , Tr/2 , N);%在[-Tp/2,Tp/2]选取采样点
%% Chirp信号生成
st = ( abs(t) < Tr/2 ) .* exp( 1j * pi * Kr * t.^2 );
f_chirp= Kr * t; %信号频率
phase_chirp = pi * Kr * t.^2;%信号相位
%% 频谱
freq = linspace(-Fs/2,Fs/2,N);%频域采样
Sf = fftshift( fft(st) );
%% 时域匹配滤波
ht = conj( fliplr(st) ); %时域匹配滤波为发射信号时间反褶再取共轭
s1 = conv(st,ht); %线性调频信号经过匹配滤波器后的输出(时域卷积)
N1 = N+N-1 ;%线性卷积后信号长度变为 N1+N2-1
t1 = linspace( -Tr/2 , Tr/2 , N1);
% 时域匹配滤波
figure,plot( t1*1e6 , abs(s1) ),xlabel('t /us'),ylabel('幅度谱'),title('时间反褶取共轭,时域卷积');
%%线性调频信号经过匹配滤波
T=10e-6; %脉冲持续时间10us
B=30e6; %线性调频信号的带宽30MHz
K=B/T; %调频斜率
Fs=10*B;Ts=1/Fs; %采样频率和采样间隔
N=T/Ts;
t=linspace(-T/2,T/2,N);
St=exp(j*pi*K*t.^2); %线性调频信号
Ht=exp(-j*pi*K*t.^2); %匹配滤波
Sot=conv(St,Ht); %线性调频信号经过匹配滤波
subplot(211)
L=2*N-1;
t1=linspace(-T,T,L);
Z=abs(Sot);Z=Z/max(Z); %归一化
Z=20*log10(Z+1e-6);
Z1=abs(sinc(B.*t1)); %辛格函数
Z1=20*log10(Z1+1e-6);
t1=t1*B;
plot(t1,Z,t1,Z1,'r.');
axis([-15,15,-50,inf]);grid on;
legend('匹配滤波','辛格');
xlabel('时间/s ');
ylabel('幅值/dB');
title('线性调频信号经过匹配滤波');
subplot(212) %展开
N0=3*Fs/B;
t2=-N0*Ts:Ts:N0*Ts;
t2=B*t2;
plot(t2,Z(N-N0:N+N0),t2,Z1(N-N0:N+N0),'r.');
axis([-inf,inf,-50,inf]);grid on;
set(gca,'Ytick',[-13.4,-4,0],'Xtick',[-3,-2,-1,-0.5,0,0.5,1,2,3]);
xlabel('时间/s');
ylabel('幅度/dB');
title('线性调频信号经过匹配滤波(补零展开之后)');
3.2.2.频域匹配滤波
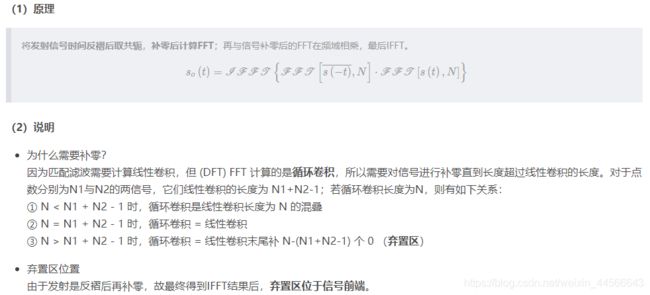
3.2.2.1.方法一
%% 频域匹配滤波1 (复制发射脉冲进行时间反褶并取共轭,计算补零DFT)
N2 = 2*N; %循环卷积长度 (N2应当>=N+N-1,其中弃置区位于长度大于N+N-1的部分)
t2 = linspace( -Tr/2 , Tr/2 , N2);
Hf2 = fft(ht,N2); %频域匹配滤波器
Sf2 = fft(st,N2);%频域信号
S2 = Sf2 .* Hf2;%频域乘积
s2 = ifft(S2);
% 频域匹配滤波1
figure,plot( t2*1e6 , abs(s2) ),xlabel('t /us'),ylabel('幅度谱'),title('时间反褶取共轭,补零FFT,频域乘积,IFFT');
3.2.2.2.方法二
%% 频域匹配滤波2(复制脉冲补零后进行DFT,对结果取复共轭(无时间反褶))
N3 = 2*N; %循环卷积长度
t3 = linspace( -Tr/2 , Tr/2 , N3);
Hf3 = conj( fft(st,N3) );% 复制脉冲补零后进行DFT,对结果取复共轭
Sf3 = fft(st,N3);
S3 = Sf3 .* Hf3;%频域乘积
s3 = fftshift(ifft(S3));
% 频域匹配滤波2
figure,plot( t3*1e6 , abs(s3) ),xlabel('t /us'),ylabel('幅度谱'),title('复制脉冲补零后FFT,取共轭,频域乘积,IFFT');
3.2.2.3.方法三
3.3.LFM脉冲压缩加窗处理
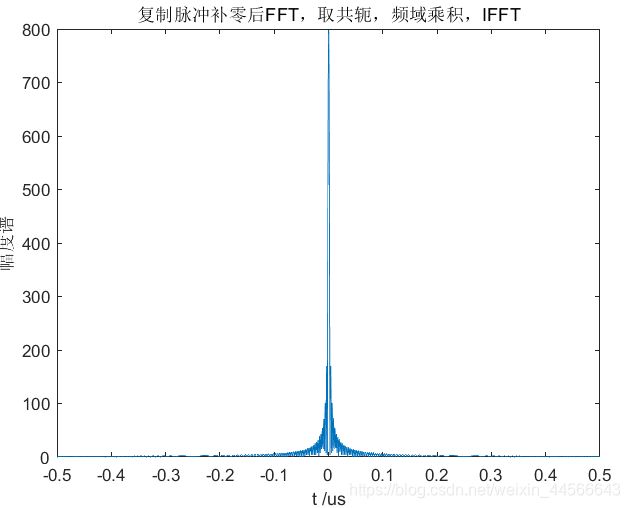
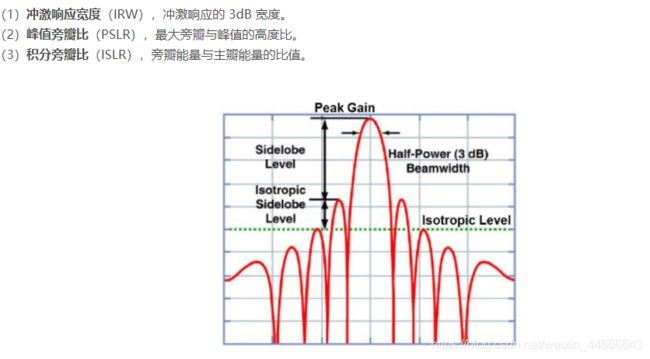
3.3.1.性能指标
3.3.2.各类窗的对比
3.3.3.脉冲压缩加窗
3.3.3.1.Hanning窗脉冲压缩加窗举例
| 没有加汉宁窗 脉冲压缩 | 加汉宁窗脉冲压缩 | 两者进行对此 |
|---|---|---|
 |
 |
 |
%%%%%%% 利用频域处理方法进行脉冲压缩 %%%%%%%
clear all
clc
clf
eps = 1e-10;
B=100e-6; %信号带宽
Fm=1e6; %调频
k=Fm/B; %调频斜率
Ts=1/(5*Fm); %采样周期
Ns=fix(B/Ts); %采样点数
Nf=1024; % fft点数
t=0:Ts:B-Ts;
y=exp(j*pi*k*t.^2); %脉冲压缩前的线形调频信号
yfft = fft(y,Nf) ;
h=zeros(1,Ns);
%% %%%%%%%%%%%%%%%%%%%%%%%%%Hamming窗%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:Ns
h(i)=conj(y(Ns-i+1));
end
hfft= fft(h,Nf); % 匹配滤波器的频域响应
lfm =abs(ifft(yfft .*hfft)); %脉冲压缩
maxval = max (lfm);
lfm = eps + lfm ./ maxval; % 利用最大值归一化
lfm_db=20*log10(lfm); %取对数
%%%%%%%%%%%%%% 加窗处理 %%%%%%%
win = hamming(Ns)';
h_w=h.*win; % 加窗
hfft_w=fft(h_w,Nf); % 加窗的匹配滤波器的频域响应
lfm_w = abs(ifft(yfft .*hfft_w)); %脉冲压缩
maxval1 = max(lfm_w);
val=lfm_w ;
lfm_w = eps + lfm_w ./ maxval; % 利用lfm的最大值归一化
lfm_w1 = eps + val./ maxval1; % 利用lfm_w的最大值归一化
lfm_w_db=20*log10(lfm_w); %取对数
lfm_w1_db=20*log10(lfm_w1); %取对数
%%%%%%%%%%%%%%%%
tt =0:Ts:2*B-Ts;
figure(1)
plot (tt,lfm_db(1:2*Ns),'b')
axis([.2*B 1.8*B -60 0] )
xlabel ('t - seconds ');
ylabel(' db')
title('没有加Hamming窗的脉冲压缩输出')
grid on
figure(2)
plot (tt,lfm_w1_db(1:2*Ns),'r')
axis([.2*B 1.8*B -60 0] )
xlabel ('t - seconds ');
ylabel(' db')
title('加Hamming窗的脉冲压缩输出')
grid on
figure(3)
plot (tt,lfm_db(1:2*Ns),'b',tt,lfm_w_db(1:2*Ns),'r')
axis([.7*B 1.3*B -60 0] )
xlabel ('t - seconds ');
ylabel(' db')
legend('未加Hamming窗','加Hamming窗');
title('脉冲压缩输出对比')
grid on
3.3.3.2.Blackman窗脉冲压缩加窗举例
| 不加窗脉冲压缩 | 加布莱克曼 | 两者对比 |
|---|---|---|
 |
 |
 |
%% %%%%%%%%%%%%%%%%%%%%%%%%%Blackman窗%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc
clf
eps = 1e-10;
B=100e-6; %信号带宽
Fm=1e6; %调频
k=Fm/B; %调频斜率
Ts=1/(5*Fm); %采样周期
Ns=fix(B/Ts); %采样点数
Nf=1024; % fft点数
t=0:Ts:B-Ts;
y=exp(j*pi*k*t.^2); %脉冲压缩前的线形调频信号
yfft = fft(y,Nf) ;
h=zeros(1,Ns);
for i=1:Ns
h(i)=conj(y(Ns-i+1));
end
hfft= fft(h,Nf); % 匹配滤波器的频域响应
lfm =abs(ifft(yfft .*hfft)); %脉冲压缩
maxval = max (lfm);
lfm = eps + lfm ./ maxval; % 利用最大值归一化
lfm_db=20*log10(lfm); %取对数
%%%%%%%%%%%%%% 加窗处理 %%%%%%%
win = blackman(Ns)';
h_w=h.*win; % 加窗
hfft_w=fft(h_w,Nf); % 加窗的匹配滤波器的频域响应
lfm_w = abs(ifft(yfft .*hfft_w)); %脉冲压缩
maxval1 = max(lfm_w);
val=lfm_w ;
lfm_w = eps + lfm_w ./ maxval; % 利用lfm的最大值归一化
lfm_w1 = eps + val./ maxval1; % 利用lfm_w的最大值归一化
lfm_w_db=20*log10(lfm_w); %取对数
lfm_w1_db=20*log10(lfm_w1); %取对数
%%%%%%%%%%%%%%%%
tt =0:Ts:2*B-Ts;
figure(1)
plot (tt,lfm_db(1:2*Ns),'b')
axis([.2*B 1.8*B -60 0] )
xlabel ('t - seconds ');
ylabel(' db')
title('没有加Blackman窗的脉冲压缩输出')
grid on
figure(2)
plot (tt,lfm_w1_db(1:2*Ns),'r')
axis([.2*B 1.8*B -60 0] )
xlabel ('t - seconds ');
ylabel(' db')
title('加Blackman窗的脉冲压缩输出')
grid on
figure(3)
plot (tt,lfm_db(1:2*Ns),'b',tt,lfm_w_db(1:2*Ns),'r')
axis([.7*B 1.3*B -60 0] )
xlabel ('t - seconds ');
ylabel(' db')
legend('未加Blackman窗','加Blackman窗');
title('脉冲压缩输出对比')
grid on
4.LFM脉冲压缩雷达测距
4.1.测距雷达的任务要求:
 |
 |
|---|
4.2.系统模型的构建
4.3.关于距离分辨率
| 两者距离 | 分辨情况 |
|---|---|
| 2m | |
| 5m | 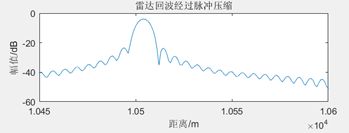 |
| 7m |  |
| 8m |  |
| 9m |  |
| 10m |  |
4.4.最终效果呈现
之后我们设置6个目标,目标的雷达截面积都为1,目标假设都为静止,我们根据雷达的相关参数设置回波窗的长度,同时根据雷达的测距范围设置6个目标物的距离,之后进行仿真,分别求出雷达回波以及经过脉冲匹配之后的结果,看是否能对目标实现测距,结果如下图所示:
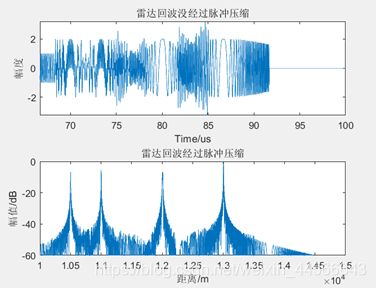
4.5.LFM脉冲压缩雷达测距matlab代码
%% LFM 脉冲多普勒雷达
%==================================================================
function LFM_radar(T,B,Rmin,Rmax,R,RCS)
if nargin==0
T=10e-6; %脉冲宽度10us
Tr=100e-6; %脉冲重复周期
B=30e6; %频带宽度30MHz
Rmin=10000;Rmax=15000; %测距范围
% R=[13000,13500];%目标点的位置,每一个目标相对于雷达的斜距
% RCS=[1,1]; %雷达截面积,一维数组
RCS=[1,1,1,1,1,1];
R=[10500,11000,12000,12008,13000,13002]; %目标点的位置,每一个目标相对于雷达的斜距
RCS=[1 1 1 1 1 1]; %雷达截面积,一维数组
end
%====================================
%%
C=3e8; %光速
K=B/T; %调频斜率
Rwid=Rmax-Rmin; %最大测距长度
Twid=2*Rwid/C; %回波窗的长度
Fs=5*B;Ts=1/Fs; %采样频率与采样时间
Nwid=ceil(Twid/Ts); %采样窗内的采样点数
%==================================================================
%%产生回拨
t=linspace(2*Rmin/C,2*Rmax/C,Nwid); %回波窗
%open window when t=2*Rmin/C
%close window when t=2*Rmax/C
M=length(R); %目标的个数
td=ones(M,1)*t-2*R'/C*ones(1,Nwid);
Srt=RCS*(exp(j*pi*K*td.^2).*(abs(td)<T/2));%从点目标来的回波
%==================================================================
%%数字信号处理 脉冲压缩
Nchirp=ceil(T/Ts); %脉冲宽度离散化
Nfft=2^nextpow2(Nwid+Nwid-1); %方便使用FFT算法,满足2的次方形式
Srw=fft(Srt,Nfft); %回波做FFT
t0=linspace(-T/2,T/2,Nchirp);
St=exp(j*pi*K*t0.^2); %线性调频信号原始信号作为参考信号
% %%加窗处理
% win=blackman(Nwid)';
% St_w=St.*win';
% %%
Sw=fft(St,Nfft); %参考信号做FFT
Sot=fftshift(ifft(Srw.*conj(Sw))); %脉冲压缩后的信号
%==================================================================
N0=Nfft/2-Nchirp/2;
Z=abs(Sot(N0:N0+Nwid-1));
Z=Z/max(Z);
Z=20*log10(Z+1e-6);
%figure
subplot(211)
plot(t*1e6,real(Srt));axis tight;
xlabel('Time/us');ylabel('幅度')
title('雷达回波没经过脉冲压缩');
subplot(212)
plot(t*C/2,Z)
axis([10000,15000,-60,0]);
xlabel('距离/m');ylabel('幅值/dB')
title('雷达回波经过脉冲压缩');
5.脉冲多普勒雷达同时实现测距测速
5.1.任务介绍
(1)这这部分之中,我们依然针对脉冲多普勒雷达来分析,之前我们研究了雷达测速问题,然而在实际问题之中我们不仅要测速,同时还要测距,都是多目标的背景,同样是用到LFM信号,脉冲压缩技术
(2)在这个小任务之中我们使用了5个目标(可以后续自行修改),牧歌目标都有各自的雷达截面积(我们是幅值都是10,相位正态随机生成),每一个目标都有自己的速度,我们生成了一个目标矩阵,目标矩阵的行数等于我发射的脉冲个数,每一行的列数取决于我采样的点数,(同时也要思考一下,在图中显示出来,发射一个脉冲的回波数最多应该是目标个数个回波脉冲,如果相邻目标物位置很近的话,我们的回波脉冲部分会重合在一起,之后再经过脉冲压缩有可能区分开)
5.2.matlab代码
clear all;clc;close all;
fc=3e9; %载波频率
PRF=2000;
Br=5e6; %带宽
fs=10*Br; %采样频率
Tp=5e-6; %脉宽
Kr=Br/Tp; %频率变化率
c=3e8; %光速
lamda=c/fc; %波长
Tr=1/PRF; %脉冲重复周期
N_mc=1.5/60*PRF; %脉冲个数
t=0:1/fs:15*Tp+Tp; %采样时间
N_r=length(t); %采样点数
N_target=5; %目标个数
Rmax=c/2*15*Tp; %目标最大距离(本来应该是1/2*c*Tr,但是采样时间限制了不可能那么大)
R_t=Rmax*abs(rand(1,N_target)); %目标的距离(这样以来目标的距离一定是小于最大距离的)
RCS_t=10*(exp(i*2*pi*rand(1,N_target))); %目标RCS,幅度为10,相位在(0,2pi)之间随机分布
Vmax=lamda*PRF/2; %目标最大速度,最大测速范围满足在第一盲速之内
v=Vmax*((1+rand(1,N_target))/2); %目标速度(这样以来目标的速度一定是小于第一盲速的),每一个目标都有一个自己的速度,对应一个矩阵
%% 生成目标矩阵
sr=zeros(N_mc,N_r); %N_mc 脉冲个数 N_r 采样点数
for i=1:N_mc
ta=(i-1)*Tr;
sri=0;%每一次从内层for循环出来之后,我们认为上一个脉冲的回波不会干扰到下一个脉冲的回波
%%内层for循环,一个目标一个目标来研究,对应每一个回波脉冲是由每一个目标回波之和组成
for k=1:N_target
tao=2*(R_t(k)-v(k).*(ta+t))/c;
srj=RCS_t(k).*rectpuls(t-tao-Tp/2,Tp).*exp(-1j*2*pi*fc*tao+1j*pi*Kr.*(t-tao-Tp/2).^2);
sri=sri+srj;
end
%%外层for循环,不同的脉冲,对应的ta是不同值,再代入来计算回波
sr(i,:)=sri;
end
%% 脉冲压缩前的回波
tm=(1:N_mc)/PRF;
R=c*t/2;
figure(1);
image(R,tm,255*abs(sr)/max(max(abs(sr))));
figure(2);
plot(t*c/2,abs(sr(1,:))); %画图我们只反映了第一个脉冲的回波情况
%% 脉冲压缩
st=rectpuls(t-Tp/2,Tp).*exp(1i*pi*Kr*(t-Tp/2).^2);%参考信号 时域 也就是匹配滤波器的时域
stf=conj(fft(st));%匹配滤波器的频域特性
for i=1:N_mc
sr(i,:)=ifft(fft(sr(i,:)).*stf); %分别对每一行脉冲压缩 频域脉冲压缩
end
figure(3);
image(R,tm,255*abs(sr)/max(max(abs(sr))))
figure;
plot(t*c/2,abs(sr(1,:)))
sr=fft(sr,[],1);
V=linspace(0,PRF,50)*lamda/2;
figure;image(R,V,255*abs(sr)/max(max(abs(sr))))
5.2.测距测速结果展示
5.2.1.情况(1)
(1)脉冲压缩前的回波
| 彩色图 image()函数 | 单色图 plot()函数 |
|---|---|
 |
 |
实际上这个时候我们就可以根据回波对应的位置知道目标所在的位置,但是很模糊,而且最重要的是,像前两个和后两个回波一样,目标位置靠的太近的话,回波实际上是会有重叠的,阴恻需要进行脉冲压缩
(2)脉冲压缩后的回波
| 彩色图 image()函数 | 单色图 plot()函数 |
|---|---|
 |
 |
我们根据plot图来用光标法来读出每一个目标点的具体位置,此处不在展开说明
(3)关于目标的速度测量

可以看出,虽然我们无法在距离维区分最近的两个目标点的位置,但是在速度维中,我们可以明显看出两者的不同进而知道是两个目标
5.2.2.其他情况
因为我们的目标点的位置和速度是随机生成的,因此应该多做几次仿真,结合工作区详细了解一下其他的情况,此处不做赘述。
6.脉冲多普勒雷达距离速度三维像
6.1.结合第五部分实现三维信息表示:
6.2.matlab代码实现
clear all;clc;close all;
fc=3e9; %载波频率
PRF=2000;
Br=5e6; %带宽
fs=10*Br; %采样频率
Tp=5e-6; %脉宽
Kr=Br/Tp; %频率变化率
c=3e8; %光速
lamda=c/fc; %波长
Tr=1/PRF; %脉冲重复周期
N_mc=1.5/60*PRF; %脉冲个数
t=0:1/fs:15*Tp+Tp; %采样时间
N_r=length(t); %采样点数
N_target=5; %目标个数
Rmax=c/2*15*Tp; %目标最大距离(本来应该是1/2*c*Tr,但是采样时间限制了不可能那么大)
R_t=Rmax*abs(rand(1,N_target)); %目标的距离(这样以来目标的距离一定是小于最大距离的)
RCS_t=10*(exp(i*2*pi*rand(1,N_target))); %目标RCS,幅度为10,相位在(0,2pi)之间随机分布
Vmax=lamda*PRF/2; %目标最大速度,最大测速范围满足在第一盲速之内
v=Vmax*((1+rand(1,N_target))/2); %目标速度(这样以来目标的速度一定是小于第一盲速的),每一个目标都有一个自己的速度,对应一个矩阵
%% 生成目标矩阵
sr=zeros(N_mc,N_r); %N_mc 脉冲个数 N_r 采样点数
for i=1:N_mc
ta=(i-1)*Tr;
sri=0;%每一次从内层for循环出来之后,我们认为上一个脉冲的回波不会干扰到下一个脉冲的回波
%%内层for循环,一个目标一个目标来研究,对应每一个回波脉冲是由每一个目标回波之和组成
for k=1:N_target
tao=2*(R_t(k)-v(k).*(ta+t))/c;
srj=RCS_t(k).*rectpuls(t-tao-Tp/2,Tp).*exp(-1j*2*pi*fc*tao+1j*pi*Kr.*(t-tao-Tp/2).^2);
sri=sri+srj;
end
%%外层for循环,不同的脉冲,对应的ta是不同值,再代入来计算回波
sr(i,:)=sri;
end
%% 脉冲压缩前的回波
tm=(1:N_mc)/PRF;
R=c*t/2;
figure(1);
image(R,tm,255*abs(sr)/max(max(abs(sr))));
figure(2);
plot(t*c/2,abs(sr(1,:))); %画图我们只反映了第一个脉冲的回波情况
%% 脉冲压缩
st=rectpuls(t-Tp/2,Tp).*exp(1i*pi*Kr*(t-Tp/2).^2);%参考信号 时域 也就是匹配滤波器的时域
stf=conj(fft(st));%匹配滤波器的频域特性
for i=1:N_mc
sr(i,:)=ifft(fft(sr(i,:)).*stf); %分别对每一行脉冲压缩 频域脉冲压缩
end
figure(3);
image(R,tm,255*abs(sr)/max(max(abs(sr))))
figure;
plot(t*c/2,abs(sr(1,:)))
sr=fft(sr,[],1);
V=linspace(0,PRF,50)*lamda/2;
V_final=255*abs(sr)/max(max(abs(sr)));
figure;image(R,V,255*abs(sr)/max(max(abs(sr))))
%%%尝试着画一下三维图
mesh(R,V,255*abs(sr)/max(max(abs(sr))));
xlabel('距离/m');
ylabel('速度/(m/s)');
zlabel('幅度/db');
title('目标信息一览');