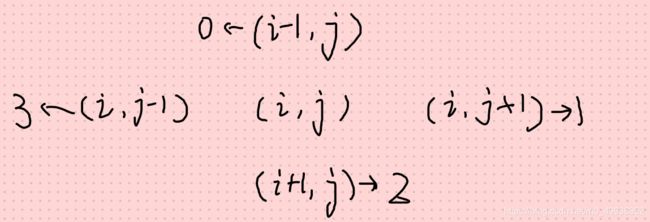迷宫问题（运用栈解决）

求迷宫中从出口到入口的所有路径，在过程中需要用到栈来存储数据结构；

下标起始值是0，从（1，1）开始走，终点是（3，4），问怎样走才能走到终点？（图画的有问题）

先从数据结构入手，需要的数据结构有栈，还有图中的点。

点的数据定义：

typedef struct {
    int x;  //行
    int y;  //列
    int next;  //下一个可走元素
}point;

栈的数据定义：

typedef struct {
    point *base;
    point *top;
    int stacksize;
}SqStack,*Stack;

其中的base和top都是指向点point这个数据结构类型的指针

说明的是,point类型中的next不能省，它用来探索路径的。

我的想法：

先将第一个点入栈，探索它的上右下左的点，

如果该点不为1，则将该点入栈，按照上右下左的顺序继续走，

如果该点为1，则将栈顶元素拿出，按照剩下的方向走

如果发现走不通，证明该点是死点，不能纳入路径中，则将该点出栈，继续将栈顶元素拿出，按照剩下的方向走。

那么如何确定行走的方向呢？

此时的next就起到了作用，

设next能取0,1,2,3，0表示它上面的点，1表示它右边的点，2表示它下面的点，3表示它左边的点

可是这个next不能显示接下来的坐标呀？

switch case在这发挥了重要作用，

switch(next){
case 0:
•   语句体   //语句体用于指明接下来的方向
case 1:
•   语句体
case 2:
•   语句体 
case 3:
•   语句体
}

总结：

先将起始点入栈，开始循环，因为后面需要不断 的入栈和出栈，因此循环条件是栈不为空，

在循环中，取栈顶元素，拿到它的坐标和next，按照上右下左的顺序，选择接下来的点，因为该点可能不是路径的点，所以需要有个变量来确认当前的点是否是活点，在本文中用find来确认，（1表示是活结点，0表示是死结点）

判断下一个点是否是活结点，如果是，就将该点（下一个点）对应的数字存储到当前点的next域中，并将该点（下一个点）入栈；

如果是死结点，则出栈，继续拿出栈顶元素，选择剩余的方向，寻找下一个可能是路径的点。

bool findWay(int i,int j,int li,int lj){
    SqStack s;
    point p,e;
    //ni,nj是下一个点的坐标，di和dj是当前点的坐标;
    //find验证下一个点是否为活结点
    int ni,nj,di,dj,find,index,next;   
    point path[100];
    InitStack(s);
    p.x=i;
    p.y=j;
    p.next=-1;
    push(s,p);
    a[i][j]=-1;
    while(s.top!=s.base){
        getTop(s,e);
        di=e.x;
        dj=e.y;
        next=e.next;
        if(di==li&&dj==lj){
            index=0;
            while(s.top!=s.base){
                pop(s,e);
                path[index++]=e;
            }
            index-=1;
            while(index>=0){
                printf("(%d,%d) ",path[index].x,path[index].y);
                index--;
            }
            return true;
        }
        find=0;
        while(next<4&&find==0){
            next++;
            switch(next){
                //从起始点的上面找
            case 0:
                ni=di-1;
                nj=dj;
                break;
                //从起始点的右边找
            case 1:
                ni=di;
                nj=dj+1;
                break;
                //从起始点的下面找
            case 2:
                ni=di+1;
                nj=dj;
                break;
                //从起始点的左边找
            case 3:
                ni=di;
                nj=dj-1;
                break;
            }
            if(a[ni][nj]==0){
                find=1;
            }
        }
        if(find==1){
            //将下一个节点对应的数字存储到当前节点的next中，当下一个点不是活结点时，用于寻找其他的点
            (s.top-1)->next=next;
            p.x=ni;
            p.y=nj;
            p.next=-1;
            push(s,p);
            //防止重复经过该点
            a[ni][nj]=-1;
        }else{
            pop(s,e);
            //因为下一个点不是活结点，需要出栈，并将图中的对应坐标的数恢复原位0
            a[e.x][e.y]=0;
        }
    }
    return false;
}

整体代码如下：

#include
#include
​
#define STACK_INT_SIZE 100
#define STACKINCREMENT 10
​
int a[6][6]={{1,1,1,1,1,1},
            {1,0,0,1,1,1},
            {1,0,0,1,0,1},
            {1,0,0,0,1,1},
            {1,1,1,0,0,1},
            {1,1,1,1,1,1}};
​
//表示点;
typedef struct {
    int x;  //行
    int y;  //列
    int next;  //下一个可走元素
}point;
​
//定义栈;
typedef struct {
    point *base;
    point *top;
    int stacksize;
}SqStack,*Stack;
​
bool InitStack(SqStack &s){
    s.base=(point *)malloc(sizeof(point)*STACK_INT_SIZE);
    if(!s.base){
        return false;
    }
    s.top=s.base;
    s.stacksize=STACK_INT_SIZE;
    return true;
}
​
bool push(SqStack &s,point e){
    if(s.top-s.base>=s.stacksize){
        s.base=(point *)realloc(s.base,sizeof(point)*(STACK_INT_SIZE+STACKINCREMENT));
        if(!s.base){
            return false;
        }
        s.top=s.base+STACK_INT_SIZE;
        s.stacksize+=STACK_INT_SIZE+STACKINCREMENT;
    }
    *s.top++=e;
    return true;
}
​
bool pop(SqStack &s,point &e){
    if(s.top==s.base){
        return false;
    }
    e=*--s.top;
    return true;
}
​
bool getTop(SqStack s,point &e){
    if(s.top==s.base){
        return false;
    }
    e= *(s.top-1);
    return true;
}
​
bool findWay(int i,int j,int li,int lj){
    SqStack s;
    point p,e;
    int ni,nj,di,dj,find,index,next;   
    point path[100];
    InitStack(s);
    p.x=i;
    p.y=j;
    p.next=-1;
    push(s,p);
    a[i][j]=-1;
    while(s.top!=s.base){
        getTop(s,e);
        di=e.x;
        dj=e.y;
        next=e.next;
        if(di==li&&dj==lj){
            index=0;
            while(s.top!=s.base){
                pop(s,e);
                path[index++]=e;
            }
            index-=1;
            while(index>=0){
                printf("(%d,%d) ",path[index].x,path[index].y);
                index--;
            }
            return true;
        }
        find=0;
        while(next<4&&find==0){
            next++;
            switch(next){
                //从起始点的上面找
            case 0:
                ni=di-1;
                nj=dj;
                break;
                //从起始点的右边找
            case 1:
                ni=di;
                nj=dj+1;
                break;
                //从起始点的下面找
            case 2:
                ni=di+1;
                nj=dj;
                break;
                //从起始点的左边找
            case 3:
                ni=di;
                nj=dj-1;
                break;
            }
            if(a[ni][nj]==0){
                find=1;
            }
        }
        if(find==1){
            (s.top-1)->next=next;
            p.x=ni;
            p.y=nj;
            p.next=-1;
            push(s,p);
            a[ni][nj]=-1;
        }else{
            pop(s,e);
            a[e.x][e.y]=0;
        }
    }
    return false;
}
​
int main(){
    int i,j,li,lj;
    findWay(1,1,4,4);
​
    return 0;
​
}