数据结构 哈夫曼树(最优二叉树) 学习心得代码
树的最后的一部分比较重要的内容
1.概念
最优二叉树,也叫哈夫曼树,是由带权结点组成的带权路径长度(WPL)最小的二叉树。注意这几个带权结点在树种都将成为叶子结点。
#include
//#define N 10
//#define M (2*N-1)
#define Maxval 32767
typedef struct {
int weight;
int parent;
int lchild;
int rchild;
}HufmTree; //哈夫曼树
typedef struct {
char bits[80];
int start;
}CodeType; //哈夫曼编码
//num是带权结点数
//road是num*2-1,即树的所有结点的数量
带权路径长度,需要进行一下计算,只有最小的才是我们这里所需要的树,它的计算公式是∑Wi Li,公式大意不重要,我们下面将举个例子,来直观的展示一下计算方法(拿上个博文中的哈夫曼树举例):
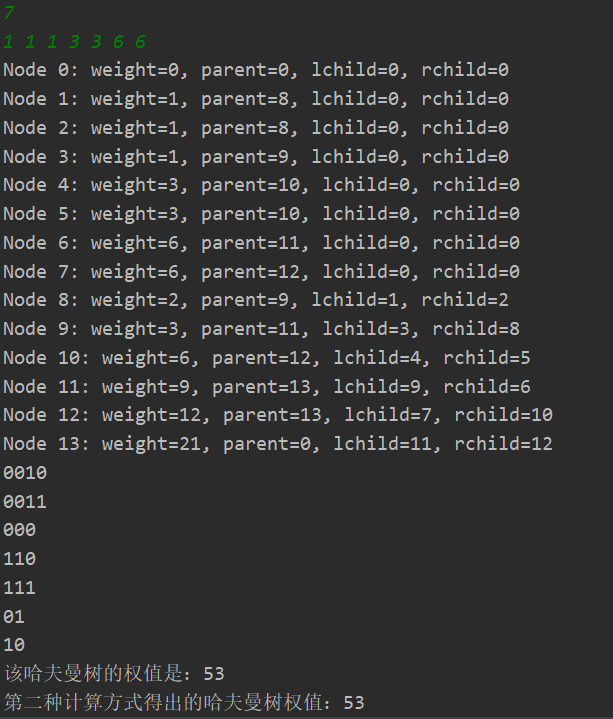
要构建该树的输入内容为(7 1 1 1 3 3 6 6,7为结点数)。
这里直接给出计算公式WPL = 1*4+1*4+1*3+3*3+3*3+6*2+6*2 = 53,可以直观的看到,计算就是对每个结点的权重乘路径长度求和,很简单对吧。另外还有一种计算方法非常简单,属于是另辟蹊径,即WPL = 2+3+6+9+12+21 = 53,即所有非叶子结点的权重相加,我们很容易的就能求到结果,不需要频繁的进行乘法,后文会同时把这两种计算方法写出。
2.哈夫曼树的构建
该树的构建无非就是找到两个权值最小的结点,然后加起来并组成他们两个的父母结点(该两个结点的parent值被置为该父母结点的下标,父母结点的下标的左右孩子值也会被置为这两个结点在数组中的下标),此处需要注意当其他结点都已经被设置好找到父母结点,就剩下根节点的情况,此时应当将根节点的parent的值设置为0(哈夫曼树的“数组”,是从1开始进行输入的,0进行了保留)。还有就是,输入前记得初始化。
void Huffman(HufmTree tree[],int num,int roads){
int i,j,p1,p2;
int small_1,small_2;
for(i = 0;i<=roads;i++){
tree[i].weight = tree[i].parent = 0;
tree[i].lchild = tree[i].rchild = 0;
}
for(i=1;i<=num;i++){
scanf("%d",&tree[i].weight);
}
for(i = num+1;i<=roads;i++){
p1 = p2 = -1;
small_1 = small_2 = Maxval;
for(j = 1;j<=i-1;j++){
if(tree[j].parent == 0){
if(tree[j].weight 3.哈夫曼编码的设置和WPL
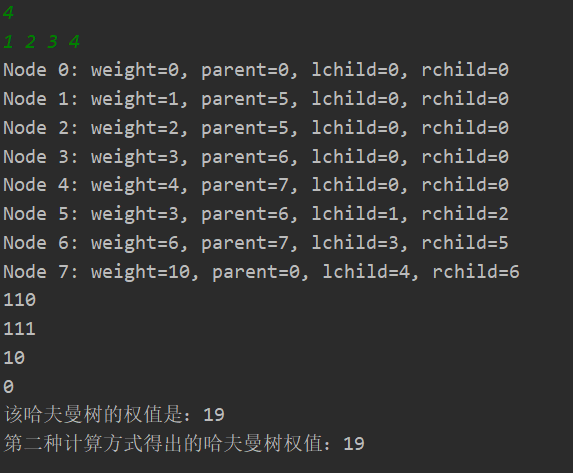
哈夫曼编码是哈夫曼树从根到该字符所在的叶结点的路径上的分支编号序列,这种编码具有短,并且为前缀码的特点。具体算法思路就是遍历每个带权结点,从后往前编码,逐渐向根移动,失语症犯了,我们直接拿例子(输入: 4 1 2 3 4)说话。
首先,我们一定知道,编码长度一定最长不过你输入的带权结点数,所以可以从bits[带权结点数]开始向前编码,设置一个变量(c)指向该结点,一个变量(p)储存其父母结点的下标,根据这个结点是其父母结点的左或者右孩子结点来赋值,之后前移,c指向该节点父母,p指向父母的父母,再次根据左右孩子复制...根据上面的内容可以得到停下的位置,带权结点数减去这个位置,即可得到这个结点哈夫曼编码长度,该长度其实也就是该结点的路径长度,所以这里可以直接在首先设置一个int变量,加和每次运算完的值,该值就是带权路径长度。(实在看不懂文字,看看代码也能懂!!!)
void HuffmanCode(HufmTree tree[],CodeType code[],int num){
int val = 0;
int i,c,p;
for(i = 1;i<=num;i++){
code[i].start = num;
code[i].bits[num] = '\0';
c = i;
p = tree[i].parent;
while(p!=0){
code[i].start--;
if(tree[p].lchild == c)
code[i].bits[code[i].start] = '0';
else code[i].bits[code[i].start] = '1';
c = p;
p = tree[p].parent;
}
puts(code[i].bits+code[i].start);
val = val + tree[i].weight * (num - code[i].start);
}
printf("该哈夫曼树的权值是:%d\n",val);
}第二种计算带权路径长度的办法上面已经讲过,此处直接用代码来阐述(talk is cheap , show you the code):
int HuffmanVal(HufmTree tree[], int num){
int val = 0;
for (int i = num+1;i<=num*2-1;i++){
val = val + tree[i].weight;
}
return val;
}
可见非常简单的几行就成功求出来了我们所需要的哈夫曼树(最优二叉树)的WPL。
4.哈夫曼函数代码以及测试用主函数
哈夫曼这里的内容大概就上面这些。下面是整个的代码,根据实际应用情况调用即可(如上题《7-1 哈夫曼编码 (PTA-数据结构)》)。
#include
//#define N 10
//#define M (2*N-1)
#define Maxval 32767
typedef struct {
int weight;
int parent;
int lchild;
int rchild;
}HufmTree;
typedef struct {
char bits[80];
int start;
}CodeType;
//HufmTree tree[M+1];
void Huffman(HufmTree tree[],int num,int roads){
int i,j,p1,p2;
int small_1,small_2;
for(i = 0;i<=roads;i++){
tree[i].weight = tree[i].parent = 0;
tree[i].lchild = tree[i].rchild = 0;
}
for(i=1;i<=num;i++){
scanf("%d",&tree[i].weight);
}
for(i = num+1;i<=roads;i++){
p1 = p2 = -1;
small_1 = small_2 = Maxval;
for(j = 1;j<=i-1;j++){
if(tree[j].parent == 0){
if(tree[j].weight 5.代码测试以及运行结果
6.后记
行文至此,树的内容算是告一段落,这些内容让我水了3个博文,还是比较难搞的,一些固定的成熟的算法还是要需要亲身去理解一下背一下,长路漫漫。在树的学习内容中,我的debug能力更上了一个台阶,大家一定要上课好好听讲,老师讲的内容往往比课下自己学的概率要高,上课内容非常有用,我的代码都是抄ppt的,大家加油!!!
return 0;//暖风迟日