2019年第八届数学建模国际赛小美赛A题放射性产生的热量解题全过程文档及程序

2019年第八届数学建模国际赛小美赛

A题 放射性产生的热量

原题再现：

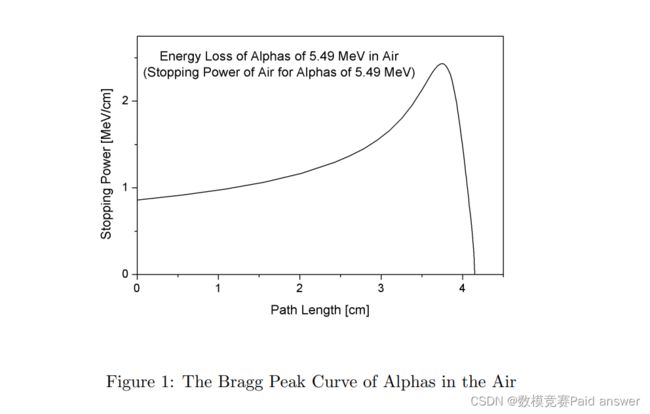
  假设我们把一块半衰期很长的放射性物质做成一个特定的形状。在这种材料中，原子核在衰变时会以随机的方向释放质子。我们假设携带质子的能量是一个常数。质子在穿过致密物质时，会释放出所携带的能量并将其转化为热量。质子的能量释放速率与其在材料中的行进距离之间的关系符合布拉格峰曲线1，即当质子行进到一定的恒定距离时，大部分能量被释放。我们把这种材料放在水中，我们可以假设质子在水中的布拉格峰曲线与材料中的相同。问题是，为了最大限度地提高材料中质子释放的总能量，材料的形状是什么？

整体求解过程概述(摘要)

  当原子核衰变时，它将沿着随机方向释放质子。质子的能量释放速率与质子在材料中的路径长度之间的关系符合布拉格峰值曲线，该曲线广泛应用于医学化疗、航空航天监测等领域。因此，研究材料的形状，最大限度地提高质子在材料中释放的总能量，具有重要的价值和意义。
  根据Mohammad Reza Rezaie[1]研究的Rn 222及其α粒子在空气、水等介质中的能量损失实验，利用实验拟合的三次多项式粒子能量方程，再现了Rn 222及α粒子在不同材料中的Bragg峰曲线分布（图3）。从Rn 222开始，证实了在小误差范围内，质子处于稠密材料中运动的布拉格峰值曲线与水中运动的合理假设相同。
  为了得到解析Bragg峰值曲线的函数方程，我们使用美国国家航空航天局空间辐射实验室现有的H55.25MeV布拉格峰值曲线的散射数据来拟合Bortfeld T[2]提出的近似函数关系。拟合可以分为上升段和下降段。通过在MATLAB中编程lsqcurvefi函数，得到能量损失方程的参数。上升段α=0.0001，p=2.1808；下降段α=0.3528，p=0.1586。
  鉴于质子能量损失的复杂性，本文主要建立了描述非弹性能量损失的方程。为了获得材料的最佳形状，碰撞方程的散射角θ近似均匀分布在[0,2],并通过蒙特卡罗方法模拟材料形状（图7）。基于上述H55.25MeV的Bragg峰曲线方程，结合Biersack[3]提出的碰撞方程的几何解，建立了碰撞参数均匀分布[0,1]的散射角θ近似方程，并用蒙特卡罗方法模拟了材料形状（图9）。
  最后，我们比较了最小二乘法和模拟退火算法对能量损失方程参数的拟合效果，其中下降段α=0.3529，p=0.1584，对比度误差在2%以内。
  本文的材料形状优化是基于H55.25MeV布拉格峰曲线的分析公式。对于α粒子（5.49MeV）在空气中的Bragg峰值曲线，上述方法也适用。

模型假设：

  本文研究的粒子是质子，在建模之前需要做以下假设[5]：
  （1） 原子的核外电子可视为静止的自由电子；
  （2） 忽略轨道大小和形状的统计波动，因为此处考虑“平均轨道”，路径视为位移。
  （3） 材料中质子的能量损失只考虑质子为高能质子，而不考虑低能质子。
  （4） 能量损失主要考虑非弹性能量损失。

问题重述：

  题目说原子核在衰变时随机释放质子。我们假设质子携带的能量是恒定的，当质子穿过致密物质本身时，质子释放出它们携带的能量并将其转化为热量。质子能量释放速率与其在材料中传播距离之间的关系符合布拉格峰曲线，即大部分能量在传播到一定恒定距离时释放。考虑到材料在水中运动与材料中的布拉格峰曲线一致，我们需要设计材料的形状，以使质子在材料中释放的总能量最大化。

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

clc,clear
close all;
%% Energy distance function curve of 222Rn in different media
figure(1);
x=0:80; 
% Air
E1=5.49-0.081.*x-0.0009333*x.^2-0.000007997*x.^3;
plot(x,E1,'LineWidth',2)
xlabel('Path Length [mm]')
ylabel('Alpha Energy [MeV]')
grid on
hold on
axis([0 60 0 6]);
% Water
E2=5.49-0.0792.*x-0.000915*x.^2-0.00000764*x.^3;
plot(x,E2,'LineWidth',2)
% Hexane
E3=5.49-0.06.*x-0.00012*x.^2-0.000012*x.^3;
plot(x,E3,'LineWidth',2)
% Cyclohexane
E4=5.49-0.07548.*x-0.000114*x.^2-0.0000204*x.^3;
plot(x,E4,'LineWidth',2)
% Olive Oil
E5=5.49-0.072.*x-0.0007*x.^2-0.0000715*x.^3;
plot(x,E5,'LineWidth',2)
% CR-39
E6=5.49-0.10148.*x-0.000589*x.^2-0.00004206*x.^3;
plot(x,E6,'LineWidth',2)
legend('Air','Water','Hexane','Cyclohexane','Olive Oil','CR-39')
%% Partial Bragg peak curve of 222Rn in different media
figure(2);
x=0:80; 
% Air
y1=-(-0.081-2*0.0009333*x-3*0.000007997*x.^2);
plot(x,y1,'LineWidth',2)
xlabel('Path Length [mm]')
ylabel('Stopping Power [MeV/mm]')
grid on
hold on
% Water
y2=-(-0.0792-2*0.000915*x-3*0.00000764*x.^2);
plot(x,y2,'LineWidth',2)
% Hexane
y3=-(-0.06-2*0.00012*x-3*0.000012*x.^2);
plot(x,y3,'LineWidth',2)
% Cyclohexane
y4=-(-0.07548-2*0.000114*x-3*0.0000204*x.^2);
plot(x,y4,'LineWidth',2)
% Olive Oil
y5=-(-0.072-2*0.0007*x-3*0.0000715*x.^2);
plot(x,y5,'LineWidth',2)
% CR-39
y6=-(-0.10148-2*0.000589*x-3*0.00004206*x.^2);
plot(x,y6,'LineWidth',2)
legend('Air','Water','Hexane','Cyclohexane','Olive Oil','CR-39')

%% Fit using the lsqcurvefit function
clc,clear
close all;
tic;
%% Ascent stage
xdata1=[0,1,1.5,2,2.25,2.4,2.5,2.525,2.55]; % unit(cm)
ydata1=[1,1.215,1.398,1.793,2.29,3.001,4.489,5.141,5.291]*1.162*10; % 
unit(MeV/cm)
canshu1=[0.1,0.1]; % Set the initial fitting point.
options=optimset('TolFun',1e-8,'TolX',1e-8,'MaxFunEvals',300,'Algorithm','trustregion-reflective','display','iter');
% The optimset command creates or edits the optimization options structure variable
% TolFun - termination tolerance for function values.
% Termination tolerance at TolX -- x.
% MaxFunEvals - maximum number of function evaluations.
% Algorithm is choosing trust-region-reflective.
% Display - Display level. Select 'off' to show no output. Select 'iter' to display the 
output of each iteration process; 
% Select 'final' to display the final result. Print the diagnostic information for the 
minimization function.
lb1=[0.0001,0.0001]; % Lower limit
ub1=[10,10]; % Upper limit
fitted_value1=lsqcurvefit(@fun,canshu1,xdata1,ydata1,lb1,ub1,options);
%% Descent stage
xdata2=[2.55,2.575,2.6,2.7,2.75,3]; % unit(cm)
ydata2=[5.291,4.349,3.412,0.032,0.001,0.001]*1.162*10; % unit(MeV/cm)
canshu2=[0.1,0.1]; % Set the initial fitting point
options=optimset('TolFun',1e-8,'TolX',1e-8,'MaxFunEvals',300,'Algorithm','trustregion-reflective','display','iter');
lb2=[0.0001,0.0001]; % Lower limit
ub2=[10,10]; % Upper limit
fitted_value2=lsqcurvefit(@fun,canshu2,xdata2,ydata2,lb2,ub2,options);
toc;
%% Visual output
R=3;
x1=0:0.05:2.55;
x2=2.55:0.05:3.00;
x=0:0.05:3;
alpha1=fitted_value1(1)
p1=fitted_value1(2)
alpha2=fitted_value2(1)
p2=fitted_value2(2)
Stopping_Power1=1./(alpha1.*p1).*((alpha1./(R-x1)).^(1-1./p1)); 
Stopping_Power2=1./(alpha2.*p2).*((alpha2./(R-x2)).^(1-1./p2)); 
if Stopping_Power1(end)>=Stopping_Power2(1)
 mid=Stopping_Power1(end);
else
 mid=Stopping_Power2(1);
end
Stopping_Power=[Stopping_Power1(1:end-1),mid,Stopping_Power2(2:end)];
plot(x,Stopping_Power,'LineWidth',1.2)
title('Fit using the lsqcurvefit function')
xlabel('Path length [cm]')
ylabel('Stopping Power [MeV/cm]')
grid on

%% Fitting using simulated annealing algorithm
clc,clear
close all;
tic;
%% Ascent stage
xdata1=[0,1,1.5,2,2.25,2.4,2.5,2.525,2.55]; % unit(cm)
ydata1=[1,1.215,1.398,1.793,2.29,3.001,4.489,5.141,5.291]*1.162*10; % 
unit(MeV/cm)
F1=@(canshu1)norm(fun(canshu1,xdata1)-ydata1);
% Canshu1 is the parameter to be fitted.
% Norm function is used to calculate the 2-norm of fun(canshu1,xdata1)-ydata1
% 2- norm square root of the sum of squares of each element
canshu1=[5,5]; % Set the initial fitting point.
lb1=[0,0]; % Lower limit
ub1=[10,10]; % Upper limit
options= saoptimset('Display','iter'); % shows the results of each optimization iteration 
(intermediate process)
[fitted_value1,fval1,exitFlag,output] = simulannealbnd(F1,canshu1,lb1,ub1,options);
%% Descent stage
xdata2=[2.55,2.575,2.6,2.7,2.75,3]; % unit(cm)
ydata2=[5.291,4.349,3.412,0.032,0.001,0.001]*1.162*10; % unit(MeV/cm)
F2=@(canshu2)norm(fun(canshu2,xdata2)-ydata2);
% Canshu2 is the parameter to be fitted.
% Norm function is used to calculate the 2-norm of fun(canshu2,xdata2)-ydata2
canshu2=[5,5]; % Set the initial fitting point.
lb2=[0,0]; % Lower limit
ub2=[10,10]; % Upper limit
options= saoptimset('Display','iter'); % shows the results of each optimization iteration 
(intermediate process)
[fitted_value2,fval2,exitFlag,output] = simulannealbnd(F2,canshu2,lb2,ub2,options);
toc;
%% Visual output
R=3;
x1=0:0.05:2.55;
x2=2.55:0.05:3.00;
x=0:0.05:3;
alpha1=fitted_value1(1)
p1=fitted_value1(2)
alpha2=fitted_value2(1)
p2=fitted_value2(2)
Stopping_Power1=1./(alpha1.*p1).*((alpha1./(R-x1)).^(1-1./p1)); 
Stopping_Power2=1./(alpha2.*p2).*((alpha2./(R-x2)).^(1-1./p2)); 
if Stopping_Power1(end)>=Stopping_Power2(1)
 mid=Stopping_Power1(end);
else
 mid=Stopping_Power2(1);
end
Stopping_Power=[Stopping_Power1(1:end-1),mid,Stopping_Power2(2:end)];
plot(x,Stopping_Power,'LineWidth',1.2,'color','r')
title('Fitting using simulated annealing algorithm')
xlabel('Path length [cm]')
ylabel('Stopping Power [MeV/cm]')
grid on

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可