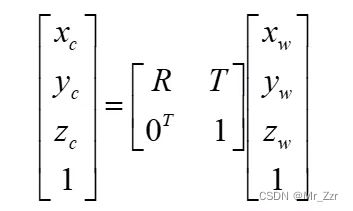机器视觉【1】相机的成像(畸变)模型
零、前言
很久没写文章,简单唠一唠。
不知道巧合还是蜀道同归,部门领导设定了些研究课题,用于公司部门员工的超前发展,该课题是“2D to 3D的三维重建”,这一块刚好是我个人看中的一个大方向,所以就有了这一系列的文章。其实我还发现不少同学是没搞清楚 什么是 机器视觉?机器视觉和图像处理的区别是什么?又有什么关联?我们来看看文心一言是怎么说的。
机器视觉是人工智能的一个分支,它利用机器代替人眼来做测量和判断。机器视觉系统通过机器视觉产品(即图像摄取装置,分CMOS和CCD两种)将被摄取目标转换成图像信号,传送给专用的图像处理系统,得到被摄目标的形态信息,根据像素分布和亮度、颜色等信息,转变成数字化信号。图像系统对这些信号进行各种运算来抽取目标的特征,进而根据判别的结果来控制现场的设备动作。机器视觉系统综合了光学、机械、电子、计算机软硬件等多方面技术,涉及到计算机、图像处理、模式识别、人工智能、信号处理、光机电一体化等多个领域。
图像处理(image processing)是一种用计算机对图像进行分析,以达到所需结果的技术。它也被称为影像处理。图像处理技术的主要内容包括图像压缩、增强复原、匹配描等。它的应用范围非常广泛,包括测绘学、大气科学、天文学、美图、使图像提高辨识等。此外,基于光学理论的处理方法依然占有重要的地位。图像处理是信号处理的子类,另外与计算机科学、人工智能等领域也有密切的关系。当前大多数的图像均是以数字形式存储,因而图像处理很多情况下指数字图像处理。图像属于二维信号,和一维信号相比,它有自己特殊的一面,处理的方式和角度也有所不同。
图像处理和机器视觉是紧密相关的两个领域。
图像处理是对图像进行各种操作,包括图像的增强、滤波、修复等,目的是让图像更美观、更易于分析。而机器视觉则是让机器能够像人类一样通过摄像头等设备来感知和理解图像的过程,它可以用来识别物体、检测运动、测量距离等。
在机器视觉中,图像处理技术被广泛应用。例如,在人脸识别过程中,首先需要对图像进行处理,提取出人脸的特征,然后再通过比对来判断是否为同一个人。这个过程中,图像处理技术起到了至关重要的作用。同时,图像处理也可以为机器视觉提供一些基础工具,如边缘检测、图像分割等技术,这些都有助于机器视觉系统更好地理解图像。
总的来说,图像处理是机器视觉的一个重要组成部分,为其提供了必要的技术手段和方法。同时,二者又各自独立,分别具有其独特的广泛应用领域。
一、成像原理——针孔相机模型
这一章主要介绍的是相机的成像原理,以及它的数学模型是如何建立的。在这个过程中我们需要了解相关坐标系的定义,以及一些畸变成像的相关内容。接下里正常进入学习环节。
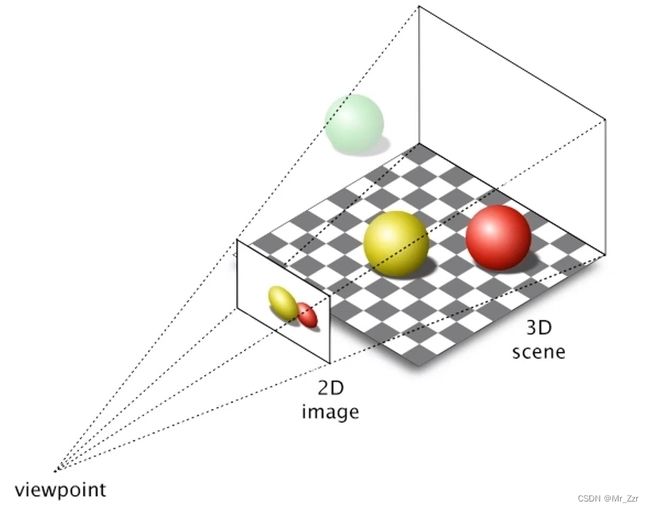
相机的作用是什么?是拍照(废话)换成专业的术语就是 对三维世界进行2D的投影变换。 对于成像之后的图片,我们是不能从图像中获取其真实的信息。譬如上图的球,在图像中我们是不知道真实的球体究竟有多大,距离有多远。
那么我们能否从2D图像中恢复三维世界的模型,从而推断其近似的真实信息?答案是可以通过多视角的方式去推算,譬如双目立体视觉就很好的进行测距计算。那么如何通过摄像机拍出的二维照片,精确的恢复三维信息?这就需要先对相机的成像过程进行数学建模,用严谨的数学表达式来描述整个成像过程。
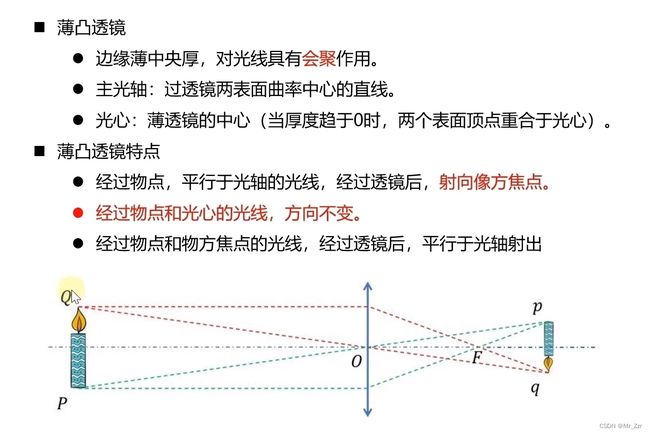
首先从镜头入手一步步的理解整个成像。一般的镜头都是通过很多层凹凸透镜的堆叠,来以修改外部光的光路进入到摄像机,但在分析镜头的过程我们一般可以等效以上的一个模型,这是一张初中物理很经典ppt,其描述了凸透镜对光路折射汇聚的特点。其中经过物体点和凸透镜光心的光线是不会改变方向,那么如果要理解整个世界中的一点到2D图像的成像点的时候,我们可以用这一简单的光线去做等效,来简化整个成像过程。
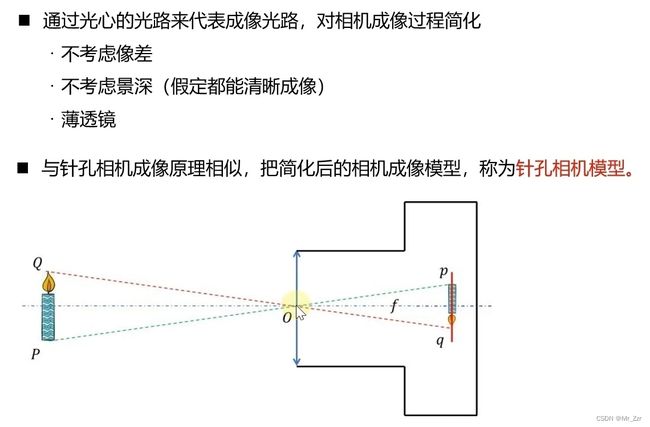
但是这个成像过程是基于一些假设的,就是说还存在一些问题点,假设成像点没有像素差;不考虑景深,能够在成像面上投影出清晰的图像。最终发现 这个成像过程 和 小孔成像的原理是一致的,因此我们可以把简化后的相机成像模型称之为针孔相机模型。
现在我们对世界的物体点 到成像的过程做了一个简化模型,下一步讨论 要如何计算世界中的物体点对应成像面上的坐标位置。
二、坐标系转换
(汇总图)
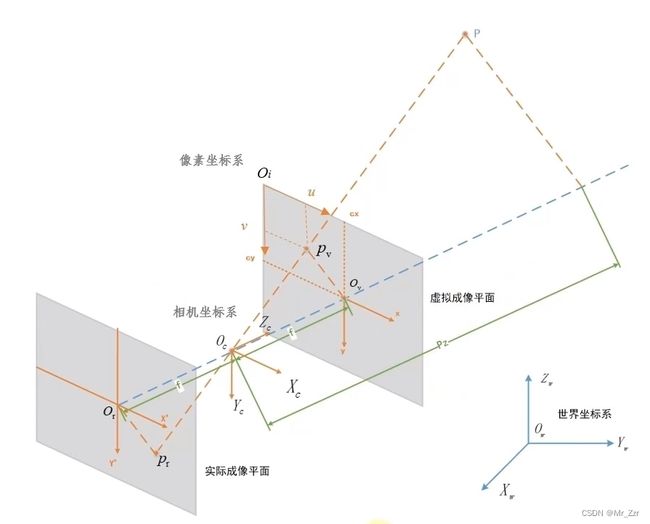
这里通过一张总图,介绍成像过程中涉及到一些坐标系,以及它们的关联。
- 世界坐标系:
以被测物体上的点作为参考,定义的绝对坐标系。坐标标记方式为Ow(Xw,Yw,Zw),也有把世界坐标系和相机坐标系定义重合为同一个坐标系上。 - 相机坐标系:
以相机光心为坐标原点,主光轴上 物体方朝焦点方向为z轴,平行于Censor平面的两条垂直边分别为x和y轴。坐标记为(Xc,Yc,Zc) - 图像坐标系:
以主光轴与sensor的交点为坐标原点,平行于sensor平面的两条垂直边分别为x和y轴,坐标纪为(x,y)这个平面是建立在实际成像面上的,是个二维坐标系 - 像素坐标系:
平行于sensor的虚拟成像平面,左上角顶点为原点xy轴都平行于图像平面,以像素为单位,坐标标记为(u,v)。
这里说说虚拟成像面和实际成像面的概念,虚拟成像面到光心的距离 等于 实际成像面与光心之间的距离,两个相互平面,经光心原点对称。为什么要定义虚拟成像面?对于世界坐标系中的一点P,它在实际成像面上的像点是Pr,在虚拟成像面上的像点是Pv,可以看到真实物体点在实际成像面是方向相反的(即倒立成像)但是在虚拟成像面的方向与真实世界坐标系就是一致的。所以在进行坐标换算的时候,方向问题就可以暂时不用去考虑了。那么讨论图像坐标系 和 像素坐标系的关系,就不难发现其实两个坐标系是一个偏移+倍率缩放的变换。
世界坐标系→相机坐标系
第一步是最简单的一步,世界坐标系转换到相机坐标系,两者其实就一个刚体变换,在上面也介绍了两者甚至可以是重合的,在实际计算两者互换的时候,搞清楚R和T的转换。详情可以到以前的文章了解矩阵的几何变换
相机坐标系→图像坐标系
第二步就是相机坐标系变换到图像坐标系,相机到图像的变换其实就是 小孔成像的物理模型,其中的数学道理其实就是两个相似三角形成正比。
即 X’ / X = f / Z
X' 是图像坐标系的横轴;X 是相机坐标系的横轴;
f 是镜头的焦距;Z就是物体像点在相机坐标系的距离;
上述給出了数学表达式,然后再转换为齐次矩阵的表达方式,到这一步还没啥特别难的部分。
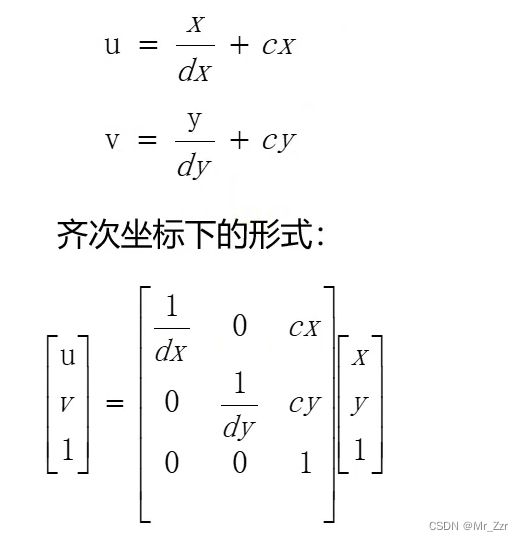
图像坐标系→像素坐标系
最后一步就是图像到像素的转换,上面也提到了,实际成像面(图像)到虚拟成像面(像素)其实是一个图像数字化的过程,它们是一个倍率和偏移的操作。用数学式表达如下
dx,dy:表示图像单个像素的宽高,单位为mm/pixel
(cx, cy):表示图像中心点的像素坐标。即主光轴与sensor平面的交点。一般在设备制作CCD转换就会有标注。没有的话,也可以通过后期标定。
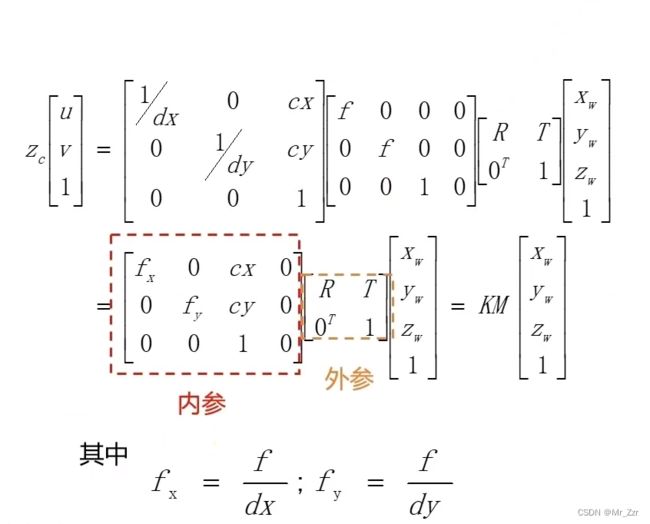
整合:世界坐标系→像素坐标系
整个转换过程如上图,该公式应该是从右往左依次解读,世界物体点通过刚体变换,通过小孔成像的原理处理后,再经过图像数字化的倍率和偏移,最终得到屏幕的像素点。我们把跟相机相关的变量合并称为内参,RT刚体变换称为外参,这就是往后需要介绍的参数标定。
可以看到它其实是一个线性变换的过程,这是一个理想化的成像过程,但实际情况并不可能有这样理想的成像过程,最普遍的在sensor的制造过程中,由于镜头的畸变,dx和dy会有偏差并不完成一致成正比。接下来看看在有畸变的情况下要如何处理。
三、畸变的产生及其数学模型
畸变其实是一种像素位置产生了偏差,是一种不会改变成像清晰度和质量的一种偏差。初学者来说畸变分为两类 径向畸变 和 切向畸变。
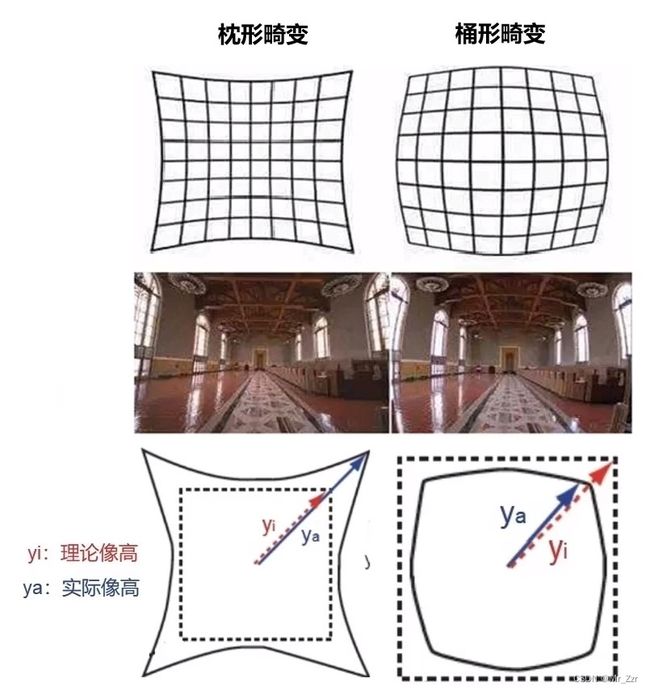
径向畸变是最常见的一种光学畸变,一般分为枕形畸变(正畸变)和桶形畸变(负畸变)越向透镜边缘移动,径向畸变越严重。如下图所示。
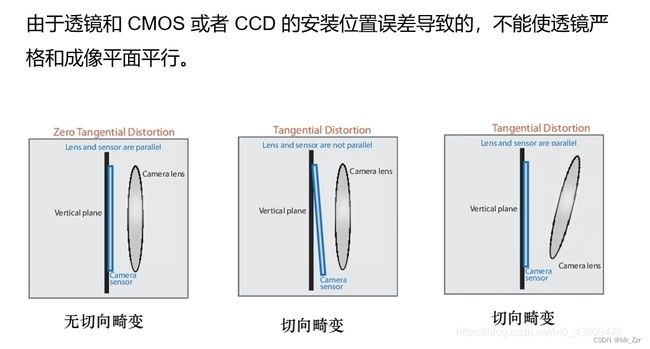
而切向畸变一般是由设备生成工艺组装阶段的误差导致,这种畸变在光学设计上是不应该存在的。理想情况下镜头lens和sensor平面应该是平行的,但实际上组装的时候无法百分之百保证这种平行,两个平面会产生小的倾斜旋转。如下图所示。
畸变的数学模型
关于畸变模型详细的推导原理,我们留着往后的章节再作讨论。现在先着重关注畸变模型对整个相机成像模型的理解。
径向畸变模型如上图所示,一般情况用K3量级去表示,OpenCV会用到K6的量级去实现。请注意,公式右边的[x,y]表示的是理想的成像点,左边[Xrd, Yrd]是实际的畸变成像点,其实这和整个标定过程是一致的,理想的成像点和实际的成像点之间存在一个加畸变的过程。从公式还可以了解到径向畸变是和图像坐标系的半径有关,其实就是和具体成像点的位置 和 主点的欧式距离相关联。
切向畸变模型,一般用P1、P2两个斜变率去表示,OpenCV也是用这个公式。
一般在去标定畸变的时候,为了消除畸变系数的尺度因素,通常约定俗成的规定理想的成像点、畸变成像点都是在单位焦平面上,什么是单位焦平面?往上翻查(汇总图)其实单位焦平面就是焦距f=1的时候,理想成像点、实际成像点所在的位置。为什么考虑在单位焦平面上做去畸变的运算呢?因为在同一个理想成像点的位置,如果摄像头的焦距不一样,实际成像点的位置也会不一样,为了消除焦距 f 这因素导致的畸变量不一样,所以统一在做去畸变的标定时要用单位焦平面,相当于是归一化的处理,这样在实际焦距发生变化的时候,畸变量乘以焦距 f 就可以了。
最后把两种畸变的数学模型合并,得到的就是常用K3畸变模型。
四、相机的标定
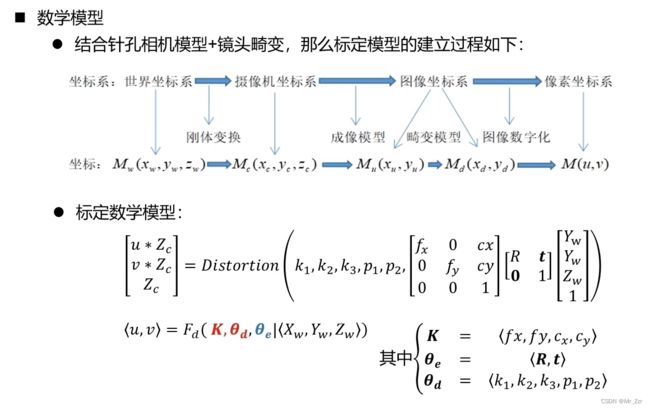
综合以上描述的所有内容,我们可以把相机的成像模型,或者说相机标定的数学模型 等价为一个理想的模型加一个误差模型,理想模型就是针孔相机模型,误差模型就是畸变引起的一个误差。结合针孔相机模型+镜头畸变,那么相机标定模型的建立过程如下图所示:
整理把整个流程总结一遍:世界坐标系中的一点,通过刚体变换到相机坐标系下,再通过小孔成像的原理到图像坐标系,然后归一化到单位焦平面上去做去畸变的处理,最后就是把图像进行一个图像数字化处理,转化到像素坐标系上。
以上过程的可以用上面的线性数学式来表达。其实所谓的标定,就是求相机的内参K、畸变参数e、以及RT变换参数d。