强化学习读书笔记

Chapter 1 Introduction

强化学习定义

智能体和环境相互交互，通过“试错（trial and error）”的方式来学习最优策略(使得奖励最大化)。
特点：

1. Trial and error search；
2. 奖励在时间上具有延迟性。

系统与环境之间的交互可以看作是马尔可夫决策过程(Markov decision process, MDP)。

监督/非监督/强化学习

机器学习技术分为三种：非监督学习、监督学习和强化学习。强化学习（RL）是一种有别于监督学习和非监督学习的在线学习技术。

1. 监督学习：situation-action（每种情况下都有一个明确对应的标签）。
2. 非监督学习：寻找隐藏在未标记数据集合中的结构。
3. 强化学习：外部环境提供少量的信息，Agent不依赖于正确行为的示例，依靠自身的经验去学习。通过学习，Agent才能获得评价，并修改自己的行动策略以适应环境。

挑战

在学习中的每一步要抉择是冒险探索（exploration），还是利用以前的经验获得当前最大的收益（exploitation）的问题。
智能体可以通过尝试非最优的动作来探索环境中未见的可能带来更大预期收益的动作和状态，也可以利用当前最优的动作来取得短期当前最大的收益，由于用于探索和利用的总次数有限，因此需要在探索和利用之间权衡。

关键特征

RL中，代理有明确的目标，能够感知环境的各个方面，并能够选择影响环境的行动。比规划问题多考虑了规划和实时行动之间的影响和环境模型的更新，和监督学习相比解释了做出决策的原因。

组成

Agent, environment, a policy, a reward signal, a value function, and, optionally, a model of the environment.
注意：

1. Policy：代理（Agent）在每一个时间步该采取什么行动。
2. Reward：强化学习的目标，外界给的对于动作到底怎么样的评价（一次，即时）。
3. Value function：agent从开始到结束时获得的期望回报（累计，长期）。
4. Model of the environment：模拟环境行为的方法，可以对环境行为进行推断。

Chapter 2 Multi-armed Bandits

评价型反馈和指导型反馈

• 评价型反馈：实际采取的动作有多好。
• 指导型反馈：应该采取什么样正确的动作。
  Evaluative feedback depends entirely on the action taken, whereas instructive feedback is independent of the action taken.

A k-armed Bandit Problem

在 RL 问题中经历多步动作之后才能观察到最终的奖励值，因此可将 RL 问题简化为多臂赌博机学习问题。
每一时刻t智能体选择某个动作At，环境返回奖励Rt，动作值定义为采取某一动作获得的期望回报：

如果知道每个动作的值，解决k-armed Bandit Problem的方法就是总是选择价值最高的动作。
但实际上，只能知道动作值估计值函数 Qt(a)，目标是其趋近动作值 。
Qt(a)最大的动作称为贪婪动作，从贪婪动作中选择，其实是利用当前最优的动作来取得短期当前最大的收益（exploitation）。如果选择了一个非贪婪操作，那就是通过尝试非最优的动作来探索（exploration），从长远来看，探索可能产生更大的总回报。

Incremental Implementation

用观察到的奖励的样本平均值来估计动作值时，如何以一种计算效率高的方式来计算这些平均值。

• 解决方法1：保存所有奖励的记录，然后在需要估算值时执行此计算，随着时间的推移，内存和计算需求会随着奖励的增加而增加。
• 解决方法2：增量公式。
  更新公式的一般形式：
  

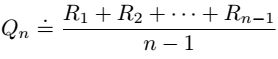
Chapter 3 Finite Markov Decision Processes

有限马尔科夫决策过程形式化

Agent-Environment

Agent: 代理，学习者和决策者。
Environment：代理交互的一切。
交互持续进行，代理选择动作，环境响应这些动作，改变状态，并向代理反馈新的状态和奖励。代理会通过它的行为选择来寻求时间累计奖励的最大化。

有限状态MDP：状态集、行为集和奖励集都是有限的元素。

状态转移概率：

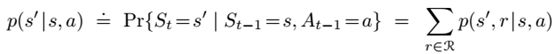
期望回报：


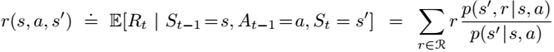
Agent与环境之间的边界通常与机器人或动物身体的物理边界不一样。
一般规则是，任何不能被代理任意更改的内容都被认为是代理环境的一部分。、
在不同的应用场景下边界可以定义在不同位置。（在一个复杂的机器人中，许多不同的代理可能同时操作，每个代理都有自己的边界。例如，一个代理可以做出高级决策，这些决策构成了执行高级决策的低级代理所面临的状态的一部分。）

Returns and Episodes

如何形式化累计奖励最大化目标。
Expected return：

Episodic tasks：
Agent与环境交互自然地分解成一系列独立的事件。将一次有限步数的实验称作一个单独的episodes，也就是经过有限步数后最终会接收一个终止状态（terminal state），这一类的任务也叫做episodic tasks。
Continuing tasks：agent和environment之间的交互不会停止，此时T=∞。
Discounted return：
γ∈[0,1]称为回报折扣因子，表明了未来的回报相对于当前回报的重要程度。γ=0时，相当于只考虑立即回报不考虑长期回报，γ=1时，将长期回报和立即回报看得同等重要。

Episodic Tasks和Continuing Tasks可以采用统一的表示：

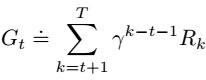
Policies and Value Functions

• Value functions: functions of states (or of state-action pairs) that estimate how good it is for the agent to be in a given state (or how good it is to perform a given action in a given state).
• Policy: 可以将策略理解为将状态映射为动作的概率分布。如果agent在t时刻遵循策略π，则π(a|s)表示在状态s下执行动作a的概率。

策略π下的状态值函数和动作值函数：


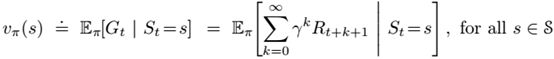
价值函数贯穿强化学习和动态规划的原因主要是它们满足特定的递推关系：

上式被称为vπ的Bellman equation，它表示了当前状态的价值函数与后续状态的价值函数之间的关系。

Optimal Policies and Optimal Value Functions

Chapter 4 Dynamic Programming

用于计算MDP的最优策略，经典的DP算法由于对模型的假设和计算量大，在增强学习中应用有限。
讨论有限MDP，使用DP找出满足Bellman最优方程的解：


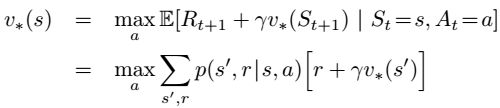
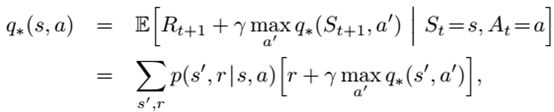
如何找：更新，逼近。

Policy Evaluation (Prediction)

问题：How to compute the state-value function vπ for an arbitrary policy π?
首先将所有的υπ(s)都初始化为0（或者任意值，但终止状态必须为0），然后采用如下公式更新所有状态s的值函数。
迭代方程：

在具体操作时，又有两种更新方法：

• 两个数组
• 一个数组

Policy Improvement

问题：由状态值函数如何找到更好的策略？
计算出状态值函数可以进一步计算动作值函数：

如果一个策略的所有动作值函数都大于另一个，那么它比较好。
计算状态值函数可以用于找到更好的策略（策略改进）。
遍历所有的状态和所有可能的动作，采用贪婪算法进行策略的更新：

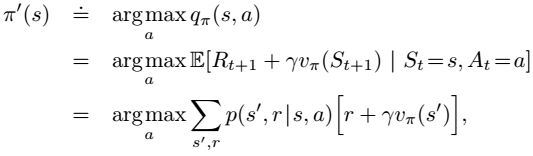
Policy Iteration

策略π通过策略改进得到一个更好的策略π′，那么我们就可以通过策略估计算法，计算策略π′的状态值函数，并进行策略改进得到一个比策略π′更好的策略π″。

Value Iteration

策略迭代的一个缺点是，它的每个迭代都涉及到策略评估，而策略评估本身可能是一个冗长的迭代计算，需要多次遍历状态集。
值迭代（value iteration）算法就是利用Bellman最优公式来提高求解效率的一种算法。
首先需要先迭代估计状态值函数，但不必每次迭代都进行策略改进。根据贝尔曼最优公式，可以直接用上一次迭代的最大动作值函数对当前迭代的状态值函数进行更新：

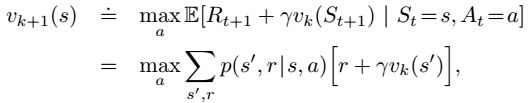
Generalized Policy Iteration

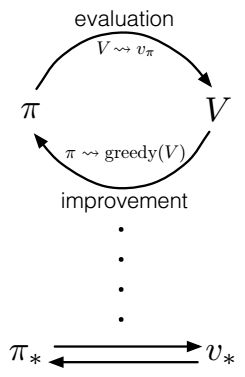
策略迭代由两个同步的、相互作用的过程组成，一个是策略评估，另一个是策略改进。
广义策略迭代（GPI）表示让策略评估和策略改进过程相互作用的一般思想。

[1]: Thrun S, Littman M L. Reinforcement Learning: An Introduction[J]. IEEE Transactions on Neural Networks, 2005, 16(1):285-286.