我的数据仓库与数据挖掘期末大作业重置版

我的数据仓库与数据挖掘期末大作业重置版

这是之前已经完成的任务，原本是我的数据仓库与数据挖掘课程的作业。里面都是比较入门的东西，没什么难度。之前学这门课的时候，上了一整个学期的课，几乎都在讲解数学原理。作为数学科目挂了四门的理工蠢材，我整个学期都听得云里雾里，到了学期末的时候突然告诉我们说期末大作业要用 Python 来写。

我当时的反应就是：

啊？

Python？

啊这，您玩儿我呢？一整个学期过去了关于 Python 的事情只字未提，现在只剩下一个星期了您跟我说要用 Python 交期末作业…… 你这样我很尴尬啊。

然后只好赶鸭子上架，学了三小时速通 Python 直接开始写报告。这个作业本来是小组作业，但是我们“小组”很尴尬地只有两个人，而学了 Python 的只有我一个。到最后只好提交了一些狗屁不通的代码（我自己都看不懂），勉勉强强把这件事情糊弄过去了。

于是我决定现在重新把这几个任务做一遍，一雪前耻。总的来说，这几个入门级别的任务还算是比较考验数据分析综合能力的（？）。

本文我希望实现的效果就是对于这四个实验能够做到事无巨细，把所有以前没有弄明白的问题全都弄懂。代码不一定都是自己写的，但是要确保自己能看懂。

希望有一定的参考价值。

准备工作

1. 安装 Python ，本次实验的版本为 Python 3.9.10
2. 在 Visual Stdio Code 中安装 Jupyter 插件，搭建开发环境
3. 使用 pip 安装需要的各种库

在终端中执行如下命令：

pip requests # http 请求库，不先安装的话后续装其他库会报错
pip install numpy pandas matplotlib scikit-learn itertools 

下面介绍各个库的功能以及用途。

数据分析老熟人：Pandas、MatPlotLib、NumPy

其中，Pandas 主要是用于从 Excel 表格中读取数据，以及对数据进行挖掘分析。官方网站为 pandas - Python Data Analysis Library
，技术文档查阅 这个链接。

matplotlib 是常见的图形库，用于绘制图表。官方网站为：Matplotlib: Visualization with Python

numpy 是常用的数学计算库。官方网站为：NumPy

itertools 是对数据进行排列组合需要用到的。
，找到的技术文档在 itertools — Functions creating iterators for efficient looping

由于本次实验需要用到大量的数学建模相关的内容，我们选择了 Python 的 scikit-learn 库，该库常用于大量的数学建模和机器学习等领域，对于完成本次任务来说非常的理想。库要求 Python 版本大于或等于 3.5 。

官方网站在 scikit-learn : Machine Learining in Python

以下是官方技术文档对于该库的介绍：

scikit-learn是基于Python语言的机器学习库，具有：

• 简单高效的数据分析工具
• 可在多种环境中重复使用
• 建立在 Numpy，Scipy 以及 matplotlib 等数据科学库之上
• 开源且可商用的 - 基于 BSD 许可

官方文档托管在 Read my Docs 平台上。关于库的更多信息，可以查阅 sklearn中文文档

预设定及导入相对应的库

库的导入

以下的几个库是四个任务中几乎都要用到的工具包。通过如下代码导入库：

" 系统相关的库 "
import os
import sys

" 数据分析相关的库 "
import numpy as np
import pandas as pd

"结果可视化"
import matplotlib.pyplot as plt
import seaborn as sns

" 用于查询概率分布表 "
from scipy import stats

" 对数据进行排列组合的库 "
import itertools

调整 Jupyter Notebook 的预设定

预设定如下，指定文档中的所有图片保存为 .svg 格式。这样的好处是可以避免图片显示模糊，同时也不需要提前设置 MatPlotLib 的图片分辨率，方便了我们的绘图。

%matplotlib inline
%config InlineBackend.figure_format = 'svg'

调整 MatPlotLib 和 Pandas 的输出设置

plt.rcParams.update(
    {
        # "figure.figsize":(8, 6),    # 画布尺寸默认 8x6
        # "figure.dpi":100,           # 图片清晰度为 100p
        "font.sans-serif":'SimHei', # 字体为黑体，否则会出现中文乱码
        "axes.unicode_minus":False, # 解决负号不显示的问题
        "image.cmap":'viridis'      # 设置颜色映射为 'viridis' 颜色表
    }
)

" pandas 设定自由列表最多为 10 行 "
# DataFrame 太长的话可能会不便于阅读
pd.options.display.max_rows = 10 

任务 1：预测问题

表 1 是 15 座城市写字楼出租率与每平方米月租金的数据。设月租金为自变量，出租率为因变量，请采用适当的回归模型进行回归预测并进行显著性检验。当显著性水平为 0.05 时，对于给定的月租金值，预测相应的出租率。

地区编号	出租率（%）	每平方米月租金（元）
1	70.6	99
2	69.8	74
3	73.4	83
4	67.1	70
5	70.1	84
6	68.7	65
7	63.4	67
8	73.5	105
9	71.4	95
10	80.7	107
11	71.2	86
12	62.0	86
13	78.7	106
14	69.5	70
15	68.7	81

数据的保存和读取

将数据保存在 ./data/forRegression.csv。表头改为英文，防止 pandas 在读取的时候出错。

# 读取数据
df_1 = pd.read_csv('./data/forRegression.csv')

# 查看数据框
df_1

	ID	rate	price
0	1	70.6	99
1	2	69.8	74
2	3	73.4	83
3	4	67.1	70
4	5	70.1	84
...	...	...	...
10	11	71.2	86
11	12	62.0	86
12	13	78.7	106
13	14	69.5	70
14	15	68.7	81

15 rows × 3 columns

数据的分析和预处理

从数据的性质上来说，这是一组非时间序列的面板数据。

由于数据点的数量连 30 都不到，进行正态检验是没有意义的。我们这里选择直接输出输出数据序列的相关性系数表：

df_1.corr() 

	ID	rate	price
ID	1.000000	0.086229	0.162063
rate	0.086229	1.000000	0.706684
price	0.162063	0.706684	1.000000

这里还可以利用 seaborn 库进行可视化，绘制相关性热力图：

mask = np.zeros_like(df_1.corr())   #定义一个大小一致全为零的矩阵  用布尔类型覆盖原来的类型
mask[np.triu_indices_from(mask)]= True      #返回矩阵的上三角，并将其设置为true
sns.heatmap(df_1.corr(), mask=mask, cmap="coolwarm", annot=True)

可以看见，这里 price 和 rate 的相关性系数大于等于 0.5，呈现显著性线性相关；

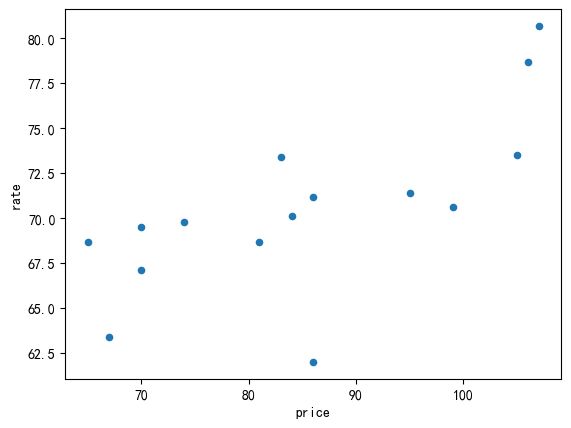
对数据进行可视化，计算数据框中各个数据序列的相关性，寻找预测依据：

# 绘制成散点图的形式
df_1[['rate', 'price']].plot(x ='price', y ='rate', kind='scatter')

数据样本点的数量实在是太少了，划分训练集和测试集的意义也不大。

模型的选择和构建

线性回归

从图中可以看出两者呈现正相关关系。因此，我们首先一元线性回归的方法。

statsmodels.api 工具包提供了线性回归分析的 OLS 工具。

import statsmodels.api as sm

整理数据。这里为 x 添加截距项的工作就是在 x 矩阵的左边增加一列 1。

x = df_1['price'].values
y = df_1['rate'].values
X = sm.add_constant(x) # 为 x 添加截距项
X, y

(array([[  1.,  99.],
        [  1.,  74.],
        [  1.,  83.],
        [  1.,  70.],
        [  1.,  84.],
        [  1.,  65.],
        [  1.,  67.],
        [  1., 105.],
        [  1.,  95.],
        [  1., 107.],
        [  1.,  86.],
        [  1.,  86.],
        [  1., 106.],
        [  1.,  70.],
        [  1.,  81.]]),
 array([70.6, 69.8, 73.4, 67.1, 70.1, 68.7, 63.4, 73.5, 71.4, 80.7, 71.2,
        62. , 78.7, 69.5, 68.7]))

线性回归模型可以表示为：

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_n{x}_n+\eta$$

其中，$y$ 是因变量，$x_1,x_2,\cdots x_n$ 是自变量， 是对应的系数，$\eta$ 是误差项。所有的 $x$ 都写为一个矩阵的形式，即：

X = [ X 1 , X 2 , ⋯ X n ] = [ x 1 , 1 x 1 , 2 ⋯ x 1 , n x 2 , 1 x 2 , 2 ⋯ x 2 , n ⋮ ⋮ ⋱ ⋮ x m , 1 x m , 2 ⋯ x m , n ] \begin{aligned} X &= [X_1, X_2, \cdots X_n] \\ &= \begin{bmatrix} x_{1, 1} & x_{1, 2} & \cdots & x_{1, n} \\ x_{2, 1} & x_{2, 2} & \cdots & x_{2, n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m, 1} & x_{m, 2} & \cdots & x_{m, n} \\ \end{bmatrix} \end{aligned} X​=[X1​,X2​,⋯Xn​]= ​x1,1​x2,1​⋮xm,1​​x1,2​x2,2​⋮xm,2​​⋯⋯⋱⋯​x1,n​x2,n​⋮xm,n​​ ​​

当我们将截距项引入模型后，可以将其视为一个额外的特征变量 $x_0$（即添加了一列 1），并且对应的系数是 ${\beta }_0$。因此，上述模型可以重写为：

$$y={\beta }_0{x}_0+{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_n{x}_n+\eta ,(x_0=1)$$

对于写成矩阵形式的 $X$，则有：

X = [ X o n e s , X 1 , X 2 , ⋯ X n ] = [ 1 x 1 , 1 x 1 , 2 ⋯ x 1 , n 1 x 2 , 1 x 2 , 2 ⋯ x 2 , n ⋮ ⋮ ⋮ ⋱ ⋮ 1 x m , 1 x m , 2 ⋯ x m , n ] \begin{aligned} X &= [X_{ones}, X_1, X_2, \cdots X_n] \\ &= \begin{bmatrix} 1 & x_{1, 1} & x_{1, 2} & \cdots & x_{1, n} \\ 1 & x_{2, 1} & x_{2, 2} & \cdots & x_{2, n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{m, 1} & x_{m, 2} & \cdots & x_{m, n} \\ \end{bmatrix} \end{aligned} X​=[Xones​,X1​,X2​,⋯Xn​]= ​11⋮1​x1,1​x2,1​⋮xm,1​​x1,2​x2,2​⋮xm,2​​⋯⋯⋱⋯​x1,n​x2,n​⋮xm,n​​ ​​

这样做的好处是，在进行参数估计和预测时，模型会考虑到数据中存在的偏移量，并提供更准确和可靠的结果。

进行回归计算：

LinearRegr = sm.OLS(y, X)
result = LinearRegr.fit()
result.summary()

D:\Python\Python39\Lib\site-packages\scipy\stats\_stats_py.py:1806: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15
  warnings.warn("kurtosistest only valid for n>=20 ... continuing "

OLS Regression Results

Dep. Variable:	y	R-squared:	0.499
Model:	OLS	Adj. R-squared:	0.461
Method:	Least Squares	F-statistic:	12.97
Date:	Sat, 21 Oct 2023	Prob (F-statistic):	0.00322
Time:	16:14:36	Log-Likelihood:	-39.328
No. Observations:	15	AIC:	82.66
Df Residuals:	13	BIC:	84.07
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
const	50.3409	5.697	8.836	0.000	38.033	62.649
x1	0.2376	0.066	3.601	0.003	0.095	0.380

Omnibus:	5.249	Durbin-Watson:	2.313
Prob(Omnibus):	0.072	Jarque-Bera (JB):	2.538
Skew:	-0.917	Prob(JB):	0.281
Kurtosis:	3.836	Cond. No.	533.

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

运行时告警：

D:\Python\Python39\Lib\site-packages\scipy\stats\_stats_py.py:1806: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15
  warnings.warn("kurtosistest only valid for n>=20 ... continuing "

这说明我们的原始数据太少了。

• 如果在 Jupyter 中使用 result.summary() 输出回归结果的总结，结果就会以 HTML 表格形式输出；

• 如果在 Jupyter 中使用 print(result.summary())，则输出是写作纯文本形式的表格。

输出模型参数：

result.params

array([50.34093838,  0.23762592])

beta_0 = result.params[0]
beta_1 = result.params[1]
beta_0, beta_1

(50.34093837916325, 0.23762591886741113)

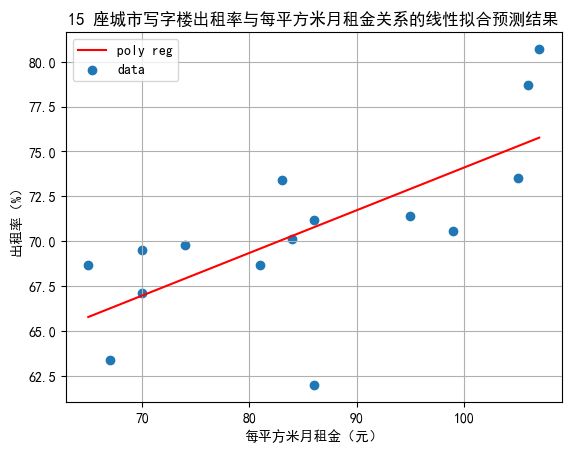
线性回归模型的可视化结果如下：

# 拟合线
plot_line = np.linspace(np.min(x), np.max(x), 100)
plt.plot(plot_line, 
         beta_0 + plot_line*beta_1, c='r', label='poly reg')
# 原始数据点
plt.scatter(x, y, label='data')
" 图例 "
plt.title("15 座城市写字楼出租率与每平方米月租金关系的线性拟合预测结果")
plt.xlabel("每平方米月租金（元）")
plt.ylabel("出租率（%）")
plt.legend()
plt.grid()

一元多项式回归

由于线性拟合结果不符合预期，所以我们可以采用一元多项式回归的方法。

多项式预测可以用下面的式子来表示：

$$y={\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2+\cdots +{\beta }_n{x}^n+ϵ$$

其中，$ϵ$ 为预测误差，即 $ϵ=\hat{y}-y$。

从而有预测模型为：

$$\hat{y}={\beta }_0+{\beta }_{1}x+{\beta }_2{x}^2+\cdots +{\beta }_n{x}^n$$

从原始数据中选择 price 和 rate 两列，作为多项式拟合的数据。

要注意：

1. 使用 DataFrame.values 将 Series 类型转为 array 类型
2. 使用 array.reshape(-1, 1) 进行数据序列的转置

x = df_1['price'].values.reshape(-1, 1)
y = df_1['rate'].values

拟合预测

导入以下几个模块。

其中，

• Pipeline 用于将数据处理的流程封装为管道
• LinearRegression 用于一元线性拟合
• PolynomialFeatures 用于多项式拟合

from sklearn.pipeline import Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

使用 Pipline 封装的数据处理流程，如下所示。要注意这里有一个多项式项数选择的问题，也就是说：我们现在不知道这个多项式应该有多少项。在这里用 degree 这个参数来设置多项式的项数；

我们设置一个变量 n 用来表示多项式的项数，则有 degree = n。

n = 8 # 多项式拟合的项数

# 使用 Pipline 封装的数据处理流程
nonLinearRegr = Pipeline([
        ( 'poly', PolynomialFeatures( degree = n ) ),
        ( 'clf', LinearRegression() )
        ])
        
# 拟合
nonLinearRegr.fit(x, y)

Pipeline(steps=[('poly', PolynomialFeatures(degree=8)),
            ('clf', LinearRegression())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. 
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

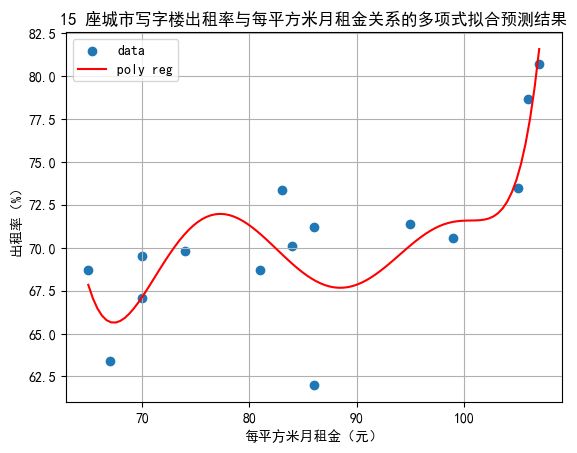
然后我们可以进行绘图，查看拟合的效果。

要注意使用 plt.plot() 进行绘图的时候，如果代入的是原始数据 x，则需要对数据点进行排序。但是在这里我直接用 np.linspace() 生成了向量空间，所以只需要进行转置然后传递给 nonLinearRegr.predict() 就可以绘制出曲线了。

" 绘图属性 "
plt.figure()
" 图线部分 "
# 原始数据点
plt.scatter(x, y, label='data')
# 拟合曲线
plot_line = np.linspace(np.min(x), np.max(x), 100).reshape(-1, 1)
plt.plot(plot_line, nonLinearRegr.predict(plot_line), c='red', label='poly reg')
" 图例 "
plt.title("15 座城市写字楼出租率与每平方米月租金关系的多项式拟合预测结果")
plt.xlabel("每平方米月租金（元）")
plt.ylabel("出租率（%）")
plt.legend()
plt.grid()

查看模型的各项参数。其中，model_params 为各个项的系数，model_intercept 为模型的截距。

使用 named_steps 找到 Pipeline 中具体的 step 的属性。

model_params = nonLinearRegr.named_steps['clf'].coef_
model_intercept = nonLinearRegr.named_steps['clf'].intercept_

print( "model params : \n", model_params )
print( "model intercept : ", model_intercept )

model params : 
 [ 0.00000000e+00  1.26935458e-02 -4.19706768e-02 -8.84001999e-01
  3.91306487e-02 -7.33777122e-04  7.12112095e-06 -3.53289531e-08
  7.11623122e-11]
model intercept :  9349.608367578356

拟合优度的评估

接下来要对模型进行拟合优度的检验：利用 sklearn.metrics 中的 r2_score 可以很容易地完成这个操作。

" 导入模块 "
from sklearn.metrics import r2_score

y_pred = nonLinearRegr.predict(x)

r2 = r2_score(y, y_pred)
print("R2 score : ", r2)

R2 score :  0.7412986594955968

下表展示了在不同的 degree 下的 R2 的值，数据来源于反复多次的测试：

degree	R2 score
0	0.0
1	0.49940
2	0.57992
3	0.65680
4	0.66935
5	0.67006
6	0.66895
7	0.66960
8	0.74130
9	0.73710

对于 degree > 9 的点，这里不再列出，因为数值不再比上述的 R2 值更小。R2 的值一般在 0 到 1 之间，越接近 1，说明模型越能解释这些数据点。从表中可以看出：当 degree = 8 的时候，R2 = 0.74130，最为理想。

故可知，模型为：

$$\begin{array}{rl}\hat{y}& =9349.608367578356\\ & +1.26935458\times 10^{-2}x\\ & -4.19706768\times 10^{-2}{x}^2\\ & -8.84001999\times 10^{-1}{x}^3\\ & +3.91306487\times 10^{-2}{x}^4\\ & -7.33777122\times 10^{-4}{x}^5\\ & +7.12112095\times 10^{-6}{x}^6\\ & -3.53289531\times 10^{-8}{x}^7\\ & +7.11623122\times 10^{-11}{x}^8\end{array}$$

自此，任务 1 完成。

任务 2：聚类分析问题

表 2 是关于西瓜的密度与甜度数据，请采用基于划分的聚类方法，将该批西瓜划分为合适的簇。

编号	密度	含糖率	编号	密度	含糖率	编号	密度	含糖率
1	0.697	0.460	11	0.245	0.057	21	0.748	0.232
2	0.774	0.376	12	0.343	0.099	22	0.714	0.346
3	0.634	0.264	13	0.639	0.161	23	0.483	0.312
4	0.608	0.318	14	0.657	0.198	24	0.478	0.437
5	0.556	0.215	15	0.360	0.370	25	0.525	0.369
6	0.403	0.237	16	0.593	0.042	26	0.751	0.489
7	0.481	0.149	17	0.719	0.103	27	0.532	0.472
8	0.437	0.211	18	0.359	0.188	28	0.473	0.376
9	0.666	0.091	19	0.339	0.241	29	0.725	0.445
10	0.243	0.267	20	0.282	0.257	30	0.446	0.459

数据的保存和读取

将数据保存在 ./data/forClustering.csv。表头改为英文，防止 pandas 在读取的时候出错。

# 读取数据
df_2 = pd.read_csv("./data/forClustering.csv")

# 查看数据框
df_2

	ID	density	sugar_rate
0	1	0.697	0.460
1	2	0.774	0.376
2	3	0.634	0.264
3	4	0.608	0.318
4	5	0.556	0.215
...	...	...	...
25	26	0.751	0.489
26	27	0.532	0.472
27	28	0.473	0.376
28	29	0.725	0.445
29	30	0.446	0.459

30 rows × 3 columns

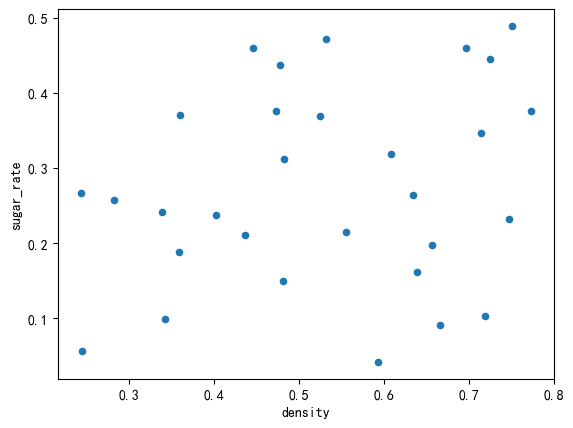
进行可视化操作，查看数据的基本情况。

df_2[['density', 'sugar_rate']].plot.scatter( x = "density", y = "sugar_rate" )

可以看见数据的分布很随机，通过肉眼观察发现没有什么聚类的依据。

我们这里选择 K-Means 算法进行聚类分析。

首先导入 sklearn.cluster 中的 KMeans 模块：

# sklearn机器学习库 cluster 聚类模块 KMeans 方法
from sklearn.cluster import KMeans

数据的分析和预处理

初始化一些变量：

" 聚类分析 "
k = 4 # 聚类的数量，可以修改数值来检验和修正聚类的结果以达到更好的预期
iteration = 500000  # 聚类最大迭代次数

选择用于聚类的数据，然后对数据进行标准化处理。

标准化是一种常见的预处理步骤，旨在将不同尺度和范围的特征转换为具有相似尺度的统一分布。

具体而言，该代码执行以下操作：

• data.mean()：计算数据的均值，即每个特征列的平均值。
• data.std()：计算数据的标准差，即每个特征列的标准差。
• (data - data.mean())：将每个数据点减去其对应特征列的均值，得到以0为中心的数据。
• (data - data.mean())/data.std()：将上述结果除以对应特征列的标准差，从而实现数据标准化。

通过标准化处理，可以消除不同尺度之间的差异，并确保所有特征都具有相似的重要性。这将有助于聚类算法更好地理解和比较各个特征，并避免某些特征对聚类结果产生过大影响。

如下面的代码所示：

data = df_2[['density', 'sugar_rate']]

data_standered = 1.0*(data - data.mean())/data.std()  # 数据标准化

# 查看标准化后的数据
data_standered

	density	sugar_rate
0	1.031876	1.403363
1	1.508603	0.767192
2	0.641827	-0.081036
3	0.480854	0.327931
4	0.158909	-0.452136
...	...	...
25	1.366204	1.622993
26	0.010319	1.494244
27	-0.354965	0.767192
28	1.205231	1.289761
29	-0.522129	1.395789

30 rows × 2 columns

聚类的实现

从而我们可以进行聚类：

# 开始聚类
cluster_model = KMeans(n_clusters = k, 
                       n_init = 'auto',
                       max_iter = iteration,
                       )  # 分为k类
cluster_model.fit(data_standered)

# 查看聚类标签和聚类中心点
labels = cluster_model.labels_
cluster_centers = cluster_model.cluster_centers_

print('labels: \n', labels)
print('cluster centers: \n', cluster_centers)

labels: 
 [1 1 2 3 2 0 2 0 2 0 0 0 2 2 3 2 2 0 0 0 2 1 3 3 3 1 3 3 1 3]
cluster centers: 
 [[-1.2318022  -0.60644501]
 [ 1.24980844  1.12465918]
 [ 0.63288406 -0.85605371]
 [-0.26132265  0.86659344]]

接下来，我们要把产生的 labels 作为一个数据序列追加到数据表格的后面。具体的做法是新建立一个名为 cluster_data 的 DataFrame，包含原始数据点的坐标和新产生的 labels。

这样做的好处是：不需要打破脑袋地调整数据的类型或者通过循环遍历的方法，把数据传递给 plt.scatter() 绘制新的彩色散点图，而是可以直接利用 pandas.DataFrame.plot.scatter() 快速绘图。

# 拼接新的列
cluster_data = pd.concat( [data, pd.Series(labels, name = "class")], axis=1)

# 查看数据
cluster_data

	density	sugar_rate	class
0	0.697	0.460	1
1	0.774	0.376	1
2	0.634	0.264	2
3	0.608	0.318	3
4	0.556	0.215	2
...	...	...	...
25	0.751	0.489	1
26	0.532	0.472	3
27	0.473	0.376	3
28	0.725	0.445	1
29	0.446	0.459	3

30 rows × 3 columns

聚类结果有效性评估

轮廓系数是一种用于衡量聚类结果质量的指标，它结合了簇内的紧密度和簇间的分离度。对于每个样本点，轮廓系数计算以下两个值：

1. $a_i$：表示样本点 $i$ 到同簇其他样本点的平均距离。这个值越小，说明样本点i与其所在簇中的其他点越相似，簇内紧密度越高。
2. $b_i$：表示样本点 $i$ 到最近非同簇样本点的平均距离。这个值越大，说明样本点i与其他簇之间的距离越大，簇间分离度越好。

基于上述定义，可以计算出每个样本点的轮廓系数：

$$s_i=\frac{b_i-a_i}{\max (a_i,b_i)}$$

其中，$s_i$ 的取值范围在 $[-1,1]$ 之间。如果 $s_i$ 接近于1，则表示样本点 $i$ 聚类得很好；如果 $s_i$ 接近于 $-1$，则表示样本点 $i$ 更应该被分配到其他簇；如果 $s_i$ 接近于 $0$，则说明样本点i在两个相邻簇的边界上。

最终，整个聚类结果的轮廓系数是所有样本点轮廓系数的均值。

从 sklearn.metrics 中导入 silhouette_samples 用于轮廓系数的计算：

from sklearn.metrics import silhouette_samples

计算轮廓系数，输出轮廓系数的平均值。

silhouetteCoefArr = silhouette_samples(data, labels)

print("Silhouette Coefficient :\n", silhouetteCoefArr)
print("Average :", silhouetteCoefArr.mean() )

Silhouette Coefficient :
 [ 0.65104246  0.64242975  0.24242421  0.00209483  0.2896085   0.35932184
 -0.07995893  0.29583778  0.6238602   0.46575515  0.51383016  0.52998268
  0.6276848   0.53971948  0.15671344  0.46917289  0.54889082  0.59270451
  0.52858366  0.51491124  0.12482582  0.49957503  0.40425347  0.62424398
  0.55266821  0.67534809  0.39026287  0.61839613  0.73527657  0.59902927]
Average : 0.45794963065432653

下表展示了在不同的 k 值下的各点轮廓系数平均值的大小：

k	Silhouette Coefficient
2	0.31616125876149975
3	0.40381864969538367
4	0.46564982452281430
5	0.42080559439960324
6	0.39701632131985300
7	0.40597256901310635

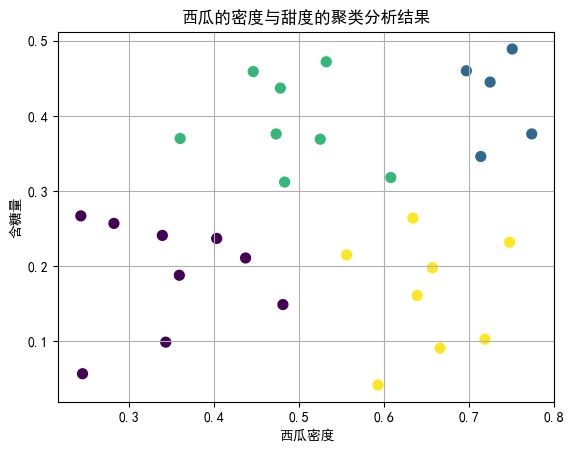
从表中可以看出，当选择 k = 4 时，轮廓系数均值最接近 1，聚类效果最好。

最后进行绘图和结果的可视化：

" 设置绘图属性 "
fig = plt.figure() # 调整图片尺寸和 DPI
ax = fig.add_subplot() # 保存给 ax，进而传递给 pandas.DataFrame.plot.scatter()

" 绘图 "
cluster_data.plot.scatter(
    x = 'density', y = 'sugar_rate', # 设置轴
    c = cluster_data['class'], # 按 class 区分颜色
    s = 50, # 点的大小
    xlabel = "西瓜密度", # 设置 X 轴标签
    ylabel = "含糖量", # 设置 Y 轴标签
    colormap = 'viridis', # matplotlib 预设的颜色
    title = "西瓜的密度与甜度的聚类分析结果", # 标题
    colorbar = False, # 不显示颜色条
    grid = True, # 显示网格线
    ax = ax # 将 ax 传递过来，实现图片大小和 dpi 的调整
    )

任务 3：Apriori 关联规则算法

考虑表 3 中显示的购物篮事务，在给定最小支持度与最小可信度的前提下，利用 Apriori 算法求出所有的频繁项集与关联规则。

事务ID	购买项
1	{牛奶，啤酒，尿布}
2	{面包，黄油，牛奶}
3	{牛奶，尿布，饼干}
4	{面包，黄油，饼干}
5	{啤酒，饼干，尿布}
6	{牛奶，尿布，面包，黄油}
7	{面包，黄油，尿布}
8	{啤酒，尿布}
9	{牛奶，尿布，面包，黄油}
10	{啤酒，饼干}

唉，这个题目有一个最奇怪的地方，就是他跟我说要求我再给定最小支持度和最小可信度的前提下，利用关联规则算法求出所有的频繁项集和关联规则。他这个话刚刚说完，然后最小支持度和最小可信度都没有给我。我就觉得挺迷惑的吧。那我这里自己取一下吧：最小支持度为 4，最小可信度为 0.4

这部分内容比较复杂。现成的 Python 模块里面没有好用的用于关联规则算法的模块；实际上，在现实生活中，像这样的关联规则算法更多地也是依据实际情况自己写的。

我们这里参考了这篇博文：用python实现Apriori算法 里面的一些代码的实现。 因为实在写得太好了，所以不得不借鉴一下。

数据的保存和读取

将数据保存在 ./data/forApriori.csv，我们用每一行数据作为一个关联项集的数据样本。如下图所示：

这里有一个技巧：关于如何读取数据的问题。

我们希望 pandas.read_csv() 在读取上述表格的时候把所有的关联项集 DataFrame 的一个列里面。

但是显然，假如我们使用：

df_3 = pd.read_csv("./data/forApriori.csv")
df_3

	牛奶	啤酒	尿布	Unnamed: 3
0	面包	黄油	牛奶	NaN
1	牛奶	尿布	饼干	NaN
2	啤酒	饼干	尿布	NaN
3	牛奶	尿布	面包	黄油
4	面包	黄油	尿布	NaN
5	啤酒	尿布	NaN	NaN
6	牛奶	尿布	面包	黄油
7	啤酒	饼干	NaN	NaN

可以看见产生的 DataFrame 包含了很多 NaN 项。不是很理想。

可以采取下面的这种方法，指定分隔符为 .csv 文件里的换行符：

df_3 = pd.read_csv(
    "./data/forApriori.csv", 
    header=None, 
    sep='\t', 
    encoding='UTF-8'
    )
df_3

	0
0	牛奶,啤酒,尿布,
1	面包,黄油,牛奶,
2	牛奶,尿布,饼干,
3	啤酒,饼干,尿布,
4	牛奶,尿布,面包,黄油
5	面包,黄油,尿布,
6	啤酒,尿布,,
7	牛奶,尿布,面包,黄油
8	啤酒,饼干,,

通过指定特定的分隔符 sep，可以划定 DataFrame 各个列的范围。这样一来，数据在 CSV 文件里面保存的每一行就都被作为一个样本点读取了。通过这种方法就能获得我们想要的数据框。

数据的分析和预处理

首先我们可以看见这里所有的数据都是以文本的形式保存的，这样非常不利于我们进行关于关联规则算法的运算。

我们现在要用数字来代替这些商品，每一种商品赋予一个数字编号，然后对这些编号进行操作。但是给商品编号并不是一件简单的事情，每个商品只能对应一种编号，编号从 1 开始到 n，n 等于商品的总数量。

要完成这样的操作，我们总共分三步：

1. 找出所有的商品，写入一个列表。每一个商品在列表中只出现一次，也就是将所有的商品一字排开。
2. 给每一种商品编号，创建一个商品和编号一一对应的字典。
3. 把原来的商品集合转化为由数字组成的数据集合，然后进行 Apriori 关联规则运算

与此同时，当我们通过关联规则计算之后，获得了新的关联数据，还要通过之前那个将数据和商品名称一一对应的字典，把数据还原成商品，查看最终的结果。

goods = []       # 用以储存商品名转换后的数字的列表
goodsList = {}   # 商品名字和数值一一对应的字典
apriori_data= [] # 转换后的数据

实际上，我们说在这里有一个细节的要注意的问题。

在本文档的开头我就说过这个项目是我之前写的数据仓库与数据挖掘的作业，第一次完成的时候因为能力不足，所以弄得很草率。这一次重新做的时候也发现了一些问题，在第一次尝试完成这个任务的作业里面有一个地方做错了。在这里提及一下，顺便分析一下这个错误产生的原因。也算是增加一些启发性的价值。

在上文中我写过，本文是参考了博文 用python实现Apriori算法 的代码实现。实际上这个事情的起因是我第一次做这个任务的时候为了尽快完成作业以便交差，直接搬运了博文里面的代码。我当时吃了不懂 Python 的亏，这次复盘的时候就发现当时的代码里面有一个错误。

我引用一下原博文的内容：原博文里面有下面的这样一组示例数据：

事务ID	购买商品
001	面包，黄油，尿布，啤酒
002	咖啡，糖，小甜饼，鲑鱼，啤酒
003	面包，黄油，咖啡，尿布，啤酒，鸡蛋
004	面包，黄油，鲑鱼，鸡
005	鸡蛋，面包，黄油
006	鲑鱼，尿布，啤酒
007	面包，茶，糖鸡蛋
008	咖啡，糖，鸡，鸡蛋
009	面包，尿布，啤酒，盐
010	茶，鸡蛋，小甜饼，尿布，啤酒

然后博文的作者把下面的一组示例数据写入了 CSV 文件，再用 data = pd.read_csv('test4-1.csv', header=None, sep='\t', encoding='UTF-8') 这样的代码指定了分隔符来读取。

面包,黄油,尿布,啤酒
咖啡,糖,小甜饼,鲑鱼,啤酒
面包,黄油,咖啡,尿布,啤酒,鸡蛋
面包,黄油,鲑鱼,鸡
鸡蛋,面包,黄油
鲑鱼,尿布,啤酒
面包,茶,糖,鸡蛋
咖啡,糖,鸡,鸡蛋
面包,尿布,啤酒,盐
茶,鸡蛋,小甜饼,尿布,啤酒

我不知道现在的阅读本文的读者有没有看出这个地方的问题。实际上，这个地方的问题还是比较明显的，就是说这个文字的组织形式不太符合常规的逗号分隔符的 .csv 文件的格式。传统的 .csv 文件为了保证列的数量是相同的，以便在 Excel 之类的表格软件中显示，对于没有任何值的行，会补上逗号。如下，是我们的数据 .csv 文件在文本编辑器里面展示的样子，可以看到在最后一列、倒数第三列存在着相邻的逗号分隔符：

牛奶,啤酒,尿布,
面包,黄油,牛奶,
牛奶,尿布,饼干,
啤酒,饼干,尿布,
牛奶,尿布,面包,黄油
面包,黄油,尿布,
啤酒,尿布,,
牛奶,尿布,面包,黄油
啤酒,饼干,,

这样一来，在 Pandas 进行读取的时候，这些没有数值的格子都会被 NaN 给填补上。

这个时候重点就来了：假如我们下面的代码是直接从原文里面复制粘贴过来的，没有任何针对 NaN 项的处理过程，那么当这些空值项通过代码的时候，是不是就会报错呢？

实际上，我亲自测试之后发现并不会。这些 NaN 项会被当做一个特殊的空商品，也被打上一个数字标签，并且合并到字典里去！空字符串所对应的商品编码会变成数字 4，这样一来，在进行关联规则统计的时候，就会多出这样没有意义的一项。

在下面的代码里面，我通过修改 if i not in goods 这一行代码为 if i not in goods and len(i) != 0，已经把这个问题给解决掉了。

我们对这里的商品进行编号：读取数据框中的列，把列里面的信息按照逗号分隔符来分割。分割之后遍历分割产生的内容，如果读取到的字符串不在商品列表里面，就将这个商品加入到商品列表里。

# 对商品进行编号
for key in df_3.values:
    key = key[0]
    key = key.split(',')
    for i in key:
        if i not in goods and len(i) != 0:
            goods.append(i)
goods

['牛奶', '啤酒', '尿布', '面包', '黄油', '饼干']

接下来，我们给每一个商品编号：我们遍历之前找到的包含所有商品名称一字排开的列表 goods，然后给每一个商品一个数字键值。

# 写入 goodList
for key in range( len(goods) ):
    goodsList[ goods[key] ] = key + 1
goodsList

{'牛奶': 1, '啤酒': 2, '尿布': 3, '面包': 4, '黄油': 5, '饼干': 6}

最后我们通过取得的这个 goodsList 字典，把原始数据转化为一个全是数值的二级列表。

具体的实现就是循环调用 appand 方法，不断在 apriori_data 列表下面追加子列表。在每一次循环开始的时候都把 key_num 列表赋值为空，然后用子循环把商品名对应的数值追加到 key_num，在外层循环结束的时候将 key_num 追加到 apriori_data

# 转换数据
for key in df_3.values:
    key_num = []
    key = key[0].split(',')

    for i in key:
        if len(i) != 0:
            key_num.append(goodsList[i])
    key_num.sort()
    apriori_data.append(key_num)
apriori_data

[[1, 2, 3],
 [1, 4, 5],
 [1, 3, 6],
 [2, 3, 6],
 [1, 3, 4, 5],
 [3, 4, 5],
 [2, 3],
 [1, 3, 4, 5],
 [2, 6]]

Apriori 关联规则算法流程设计和计算

让我们来整理一下 Apriori 关联规则算法的流程。

初始化：生成候选 1 项集

首先，我们第一步要先生成候选项集，然后判断候选项集中的每一项在原集合中的出现次数；

第二步，我们将候选项集中的每一项在原集合中的出现次数与最小支持度计数相比较，如果大于最小支持度计数，就把这个候选相机记录为频繁项集，记录下这个频繁项集的支持度

第三步，循环迭代，生成候选 1 项集到 n 项集，直到发现在上一步迭代的时候，没有产生任何频繁项集为止

流程图如下所示：

继续遍历

是

否

完成遍历

是

开始

获取全部关联项集

根据上回合频繁项集还能生成候选项集吗

生成候选项集

遍历候选项集

计算支持度计数

大于最小支持度计数吗

计入频繁项集

结束

否

确定了算法的流程就可以进行算法的实现了。不过在此之前，还有一个问题，就是我们该如何生成候选项集呢？

这里显然要用到排列组合的方法，也就是说：

1. 如果是从头开始执行算法，那么第一个候选项集就是原始的数据集里面所有的商品一字排开
2. 如果是在算法的某一级循环当中，那么候选项集就要取上一次循环里的所有频繁项集的排列组合

显然，如果我们想要写一个循环的话，就要遍历从候选 1 项集到候选 n 项集的所有情形。在这种情况下，实际上就是要首先指定生成的候选项集的每一项里面包含了商品的个数（也就是说，当生成候选 i 项集的时候，要把参数 i 传入），然后按照每一项里面的商品个数 i 把我们传入的数据集进行排列组合。

这里调用了 itertools 库里的组合方法 combinations(p,r)

• p 是一个list参数
• r 是数字，r 长度的 tuple 对象，按顺序排列，没有重复元素

这里要求 r 要小于 p 的长度。如果不小于，那么方法也会正常执行，只不过返回的是空的对象。

为了说明这个方法是如何进行排列组合的，请看下面的示例代码：

# 用于排列组合的示例列表 list_1
list_1 = [1, 2, 3, 4]
# 取 list_1 的组合，并转换成 list
list_2 = list( itertools.combinations(list_1, 3) )
print(list_2)

[(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4)]

可以看到我这里对于列表 1 进行了排列组合，生成了列表 2。

同时，在代码当中，我们对排列组合的结果取了 list()，之所以这样做，是因为如果不转化成 list，结果返回的是对象地址，而不是组合好的 tuple 对象。

print(itertools.combinations(list_1,3))

接下来我们就可以写出这个用于生成候选项集的函数了。

因为这个函数是要用在 Apriori 关联规则算法的大循环里面的，所以我们给到一个参数 i，参数 i 代表的是关联规则算法的循环迭代次数，同时也代表生成的项集是候选 i 项集。

# separate 函数用于将 data 中的数据进行排列组合，i 是组合的大小
# 作用是生成候选项集
# 简单的来说，当 i = n 的时候，产生 n 项集的随机组合
def separate(data, i):
    a = []
    b = []
    # 故技重施
    # 创建一个所有项只出现一次的一字排开的列表
    for k in data:
        for j in range(len(k)):
            if k[j] not in a:
                a.append(k[j])
    
    # 当迭代循环的次数
    # 小于等于可以用于重新组合的列表项个数的时候
    # 执行下面的操作
    # （如果不这样操作，就会产生空列表对象加入 b）
    # （b 会变成双层列表）
    if i <= len(a):
        for k in itertools.combinations(a, i):
            b.append( list(k) )
    return b

下面就是 Apriori 关联规则算法最核心的部分。我把注释写得非常详细以便人可以看得懂。

这里用到了递归的方法来优化代码：

" Apriori 算法 "
# 其中 s 是最小支持度, data 是数据集, data_iter 是迭代中的数据集,
# c 是输出的频繁项集, s 是频繁项集对应的支持度
def apriori(s_min, data, data_iter, s = [], c = [], i = 1):
    if len(data_iter) != 0: # 上回合频繁项集不为空时
        goods = separate(data_iter, i) # 生成候选项集
        data_iter = [] # 初始化用于迭代的数据集为空
        for good in goods:
            num = 0 # 初始化候选项集支持度计数为 0
            for key in data:
                if set(good) <= set(key):
                # set() 函数为 Python 内置的函数
                # 创建一个无序不重复元素集
                # 可进行关系测试，删除重复数据
                # 还可以计算交集、差集、并集等
                    num = num + 1 # 计数候选项集在原始数据里的出现次数
            if num >= s_min: # 如果出现次数大于最小支持度计数
                c.append(good) # 计入频繁项集
                s.append(num) # 同时记录这一频繁项集支持度
                data_iter.append(good)
                # 频繁项集计入用于迭代的 data_iter
                # c 保存的是所有的频繁项集
                # 而 data_iter 保存的是本轮的频繁项集
                # 在循环开始的时候清空
                # 如果进入递归就会导致死循环
        # 递归
        # i 是候选项集的项数
        # 从频繁 1 项集遍历到频繁 n 项集
        # 直到无法生成频繁 n 项集，即 data_iter = []
        print("第", i, "次迭代：", c)
        apriori(s_min, data, data_iter, s, c, i = i + 1)
    return c, s

这段代码除了实现了功能之外，还非常巧妙地用到了 Python 内置的一个 set() 函数。这个东西因为平时使用比较少，所以很多人可能不知道这个东西是干什么用的。以下是对 set() 的简单介绍：

set() 函数创建一个无序不重复元素集，可进行关系测试，删除重复数据，还可以计算交集、差集、并集等。

语法：

class set([iterable])

参数说明：iterable - 可迭代对象对象

返回值：返回新的集合对象

简单的使用方法可以参考这个快速教程链接 Python set () 函数 | 菜鸟教程

接下来我们就可以进行 Apriori 关联规则算法的计算了。我们这里选择最小支持度计数为 4 查找频繁项集：

C = []
S = []
#设置最小支持度为4
C, S = apriori(4, apriori_data, apriori_data, S, C)

第 1 次迭代： [[1], [2], [3], [4], [5]]
第 2 次迭代： [[1], [2], [3], [4], [5], [1, 3], [4, 5]]
第 3 次迭代： [[1], [2], [3], [4], [5], [1, 3], [4, 5]]

关联规则挖掘和输出结果的分析

查看一下计算的结果：

列表 C 保存了所有的关联项集

C

[[1], [2], [3], [4], [5], [1, 3], [4, 5]]

列表 S 保存的是每个项集的支持度计数

S

[5, 4, 7, 4, 4, 4, 4]

然后我们通过之前保存的字典 goodsList，把我们的关联规则，算法运行的结果恢复成商品名的二维列表。

C1 = []
for value in C:
    a = []
    for i in value:
        a.append(list(goodsList.keys())[list(goodsList.values()).index(i)])
        # keys() 方法返回 view 对象。这个视图对象包含列表形式的字典键。
        # values()函数返回一个字典中所有的值。
    C1.append(a)
C1

[['牛奶'], ['啤酒'], ['尿布'], ['面包'], ['黄油'], ['牛奶', '尿布'], ['面包', '黄油']]

在上述代码里面我们可以看到，在这段代码里面有一个非常奇怪的表述，是这个样子的：

list(goodsList.keys())[list(goodsList.values()).index(i)]

这个代码因为写得太长了，导致不好理解，让我来解释一下这个代码的意思：

• goodsList.keys() 和 goodsList.values() 都是字典对象的方法，分别返回的是字典的键和值。对于我们这里的 goodsList，返回的就是按顺序排列的商品名和商品的数字编号
• list(goodsList.values()) 把返回的字典的值转化为了一个列表对象，然后通过列表对象的 .index() 方法返回了列表中值为 i 的值的项的下标
• list(goodsList.keys()) 把返回的字典的键也转化为了一个列表对象。后面的方括号表示取下标为方括号里面的值的列表对象，而方括号里面的值就是我们之前说的商品数字编号列表中值为 i 的值的项的下标

总的来说，这行代码的原理就是通过使用字典的两种不同的方法，制造出商品数字编号列表和商品名称列表两个列表，然后通过查找商品编号列表中数值等于 i 的项所在的下标去定位这个下标所对应的商品编号所对应的商品名称。这行代码可以说是非常的七拐八绕，但是确实用一行代码就实现了七拐八绕的功能。

因为这段代码下面还会反复出现，实现的功能也是相同的，所以我这里声明一下，防止在后文当中看不懂。

我们来看一下现在的输出结果：

print('- 支持度：', S)
print('- 频繁项集：', C)
print('- 对应的商品：', C1)
print()
print('各个频繁项集的支持度：')
for i in range(len(C1)):
    print("  ", C1[i], '的支持度:', S[i])

- 支持度： [5, 4, 7, 4, 4, 4, 4]
- 频繁项集： [[1], [2], [3], [4], [5], [1, 3], [4, 5]]
- 对应的商品： [['牛奶'], ['啤酒'], ['尿布'], ['面包'], ['黄油'], ['牛奶', '尿布'], ['面包', '黄油']]

各个频繁项集的支持度：
   ['牛奶'] 的支持度: 5
   ['啤酒'] 的支持度: 4
   ['尿布'] 的支持度: 7
   ['面包'] 的支持度: 4
   ['黄油'] 的支持度: 4
   ['牛奶', '尿布'] 的支持度: 4
   ['面包', '黄油'] 的支持度: 4

接下来，我们通过下面的这个函数定义来实现一下关联规则挖掘。

关联规则挖掘的逻辑是这样的：对于一个关联项集，取出其中的每一项，计算这一项在这个关联项集合中的置信度（支持度计数与这个集合的支持度计数的比值）。如果这一项的支持度计数与这个集合的支持度计数的比值（置信度）大于等于我们预设的最小置信度，就可以认为这个元素和这个关联项集里的其他元素呈现出关联规则。

#根据频繁项集获取关联规则
# c 是最小置信度，S 是置信度列表，C 是频繁项集
def get_associationRules(c, S, C, goodList):
    for key in C:
        a = [] # 用于保存需要测算关联规则的商品的编号
        b = [] # 用于保存需要测算关联规则的商品的名称
        if len(key) > 1: # 当 C 中的频繁项集不止一个元素时
            for i in key: # 遍历 len > 1 的频繁项集
                a.append([i]) # 把每个频繁项添加到 a，对应的中文商品名存入 b
                b.append(
                    list(
                        goodList.keys()
                        )[
                            list(
                                goodList.values()
                                ).index(i)
                            ]
                    )
 
            for a_value in a: # 对于这个频繁项集中的每一项
                a_value_c = S[C.index(a_value)] # 取其作为频繁 1 项集时的支持度
                key_c = S[C.index(key)] # 再取这个频繁 n 项集的支持度

                if key_c / a_value_c >= c: # 如果支持度比值大于置信度
                    value = list(
                        goodList.keys()
                        )[
                            list(goodList.values()
                                 ).index(a_value[0]
                                )
                            ]
                    d = b.copy() # 这里需要用 .copy() 方法而不是直接赋值
                    d.remove(value) 
                    # 去掉这个项集里面的原 value 得到的就是关联规则
                    # 最后输出结果
                    print('  ', [value], ' ---> ', d, ' : ', key_c / a_value_c) 

在上面的代码里面有一些需要注意的地方，比如这里使用了 d = b.copy()。这是因为在 Python 里面，列表直接赋值得到的是引用，而不是等值的列表。如果直接赋值，那么对 d 的任何操作都会直接对 b 产生相同影响。（虽然这是一个常识，但是我还是为了防止有人忘记或者不知道，所以在这里声明一下。）

# 输出关联规则
print('关联规则 - 置信度按 0.4 计算：')
get_associationRules(0.4, S, C, goodsList)

关联规则 - 置信度按 0.4 计算：
   ['牛奶']  --->  ['尿布']  :  0.8
   ['尿布']  --->  ['牛奶']  :  0.5714285714285714
   ['面包']  --->  ['黄油']  :  1.0
   ['黄油']  --->  ['面包']  :  1.0

这就是我们关联规则挖掘的最终结果了。

任务 4：层次分析法决策问题

某高校正在进行教师的评优工作，现应用层次分析法对待评教师的综合素质进行评价。整个层次结构分为三层，最高层即问题分析的总目标，要评选出优秀教师A；第二层是准则层，包括三种指标学识水平 C1、科研能力 C2、教学工作 C3；第三层是方案层，即参加评优的教师，假设对五位候选教师 P1、P2、P3、P4、P5 进行评优，其中 P2、P3、P4 为任课教师，需要从学识水平、科研能力、教学工作三方面评估其综合素质，教师 P5 是科研人员，只需从学识水平、科研能力两方面衡量其综合素质，教师 P1 是行政人员，只需从学识水平和教学工作两方面衡量。

三个评价指标的相对重要程度不同，并且各位教师在三个指标上表现不同，具体如下：

• 科研能力指标比学识水平指标明显重要
• 教学工作指标比学识水平指标稍微重要
• 科研能力指标比教学工作指标稍微重要。

在学识水平上：

• P1 稍微高于 P2，P1 明显高于 P3
• P1 比 P4 处于稍微高与明显高之间
• P1 强烈高于 P5，P2 稍微高于 P3
• P2 比 P4 处于同样高与稍微高之间
• P2 明显高于 P5，P3 比 P5 处于同样高与稍微高之间
• P4 比 P3 处于同样高与稍微高之间
• P4 稍微高于 P5；

在科研能力上：

• P3 强烈高于 P2
• P4 稍微高于 P2
• P5 明显高于 P2
• P3 明显高于 P4
• P3 比 P5 处于同样高与稍微高之间
• P5 稍微高于 P4

在教学工作上：

• P1 稍微高于 P3
• P1 稍微高于 P4
• P2 稍微高于 P3
• P2 稍微高于 P4
• P1 与 P2 水平相当
• P3 与 P4 水平相当。

请采用层次分析法对候选教师的综合素质进行评价排序。

层次分析法的准则构造

由于题干条件已经给出了层次准则构造的要求，这里就不需要进行自主设计了。

根据题干条件，对于上述问题，层次分析准则构造如下：

方案层

准则层

目标层

P1

P2

P3

P4

P5

学识水平

科研能力

教学工作

优秀教师

建立层次结构模型

构造判断矩阵就是通过各要素之间相互两两比较，并确定各准则层对目标层的权重。

简单地说，就是把准则层的指标进行两两判断，通常我们使用 Santy 的 1-9 标度方法给出。这一标度方法的结论源于心理学对于人评估某一问题程度的行为的研究，参考如下的表格：

因素 i 比因素 j	量化值
同等重要	1
稍微重要	3
较强重要	5
强烈重要	7
极端重要	9
两相邻判断的中间值	2，4，6，8

实际上，层次分析法里面构造矩阵的方式，可以想象为一个二维表。每一行和每一列都代表一个比较的对象；我们拿每一行的对象和每一列相比较，然后参照上面的准则表，相应的数字填到矩阵里面。打个比方说，比如我们这里想要构造教学工作、学识水平和科研能力三个指标的准则矩阵，那么我们可以这样比较：首先我们拿教学工作和学识水平相比较，根据题干条件的意思，教学工作指标与学识水平指标稍微重要，然后我们把“稍微重要”代入到上面的准则表里面，可以查到稍微重要所对应的量化值为 3，我们就把数字 3 填入到矩阵的第一行第二列里面，第一行代表的就是教学工作指标，而第二列就是学识水平指标。那么这个位置就表明“教学工作指标与学识水平指标相比较”。

层次分析矩阵构造如下：

首先是准则矩阵：

C c r i t e r i a ( 1 1 5 1 3 5 1 3 3 1 3 1 ) C_{criteria} \begin{pmatrix} 1 & \dfrac{1}{5} & \dfrac{1}{3} \\ 5 & 1 & 3 \\ 3 & \dfrac{1}{3} & 1 \\ \end{pmatrix} Ccriteria​ ​153​51​131​​31​31​ ​

可以看到，像这样构造出来的矩阵，所有对角线上的元素都是一，这是因为所有对角线上的元素代表的都是每一个准则，自身和自身比较，所以重要性是完全相等的，同时也可以看到对角线两侧的元素互为倒数，这是因为如果一个指标比另一个指标稍微重要，那么另一个指标比这个指标就是“稍微重要”的倒数。

然后是方案矩阵：

C 1 = ( 1 2 5 4 7 1 2 1 3 2 5 1 5 1 3 1 1 2 2 1 4 1 2 2 1 3 1 7 1 5 1 2 1 3 1 ) C_1 = \begin{pmatrix} 1 & 2 & 5 & 4 & 7 \\ \dfrac{1}{2} & 1 & 3 & 2 & 5 \\ \dfrac{1}{5} & \dfrac{1}{3} & 1 & \dfrac{1}{2} & 2 \\ \dfrac{1}{4} & \dfrac{1}{2} & 2 & 1 & 3 \\ \dfrac{1}{7} & \dfrac{1}{5} & \dfrac{1}{2} & \dfrac{1}{3} & 1 \\ \end{pmatrix} C1​= ​121​51​41​71​​2131​21​51​​531221​​4221​131​​75231​ ​

C 2 = ( 1 1 7 2 3 1 5 7 1 5 2 3 1 5 1 1 3 5 1 2 3 1 ) C_2 = \begin{pmatrix} 1 & \dfrac{1}{7} & \dfrac{2}{3} & \dfrac{1}{5} & \\ 7 & 1 & 5 & 2 & \\ 3 & \dfrac{1}{5} & 1 & \dfrac{1}{3} & \\ 5 & \dfrac{1}{2} & 3 & 1 & \\ \end{pmatrix} C2​= ​1735​71​151​21​​32​513​51​231​1​​ ​

C 3 = ( 1 1 3 3 1 1 3 3 1 3 1 3 1 1 1 3 1 3 1 1 ) C_3 = \begin{pmatrix} 1 & 1 & 3 & 3 & \\ 1 & 1 & 3 & 3 & \\ \dfrac{1}{3} & \dfrac{1}{3} & 1 & 1 & \\ \dfrac{1}{3} & \dfrac{1}{3} & 1 & 1 & \\ \end{pmatrix} C3​= ​1131​31​​1131​31​​3311​3311​​ ​

根据题干条件的要求：教师 P5 是科研人员，只需从学识水平、科研能力两方面衡量其综合素质，教师 P1 是行政人员，只需从学识水平和教学工作两方面衡量。这就导致了我们所书写的矩阵 C2 和 C3 都只有四行四列。

通过 Python 计算 APH 层次分析法

我们这里需要整理一下层次分析法的思路：

首先我们的数学过程是先对三个矩阵进行一致性检验。在一般情况下，层次分析法中的判别矩阵都是人根据主观判断写的，因此可能会出现逻辑上的错误。比如矩阵中有A、B、C三个元素的比较，可能会因为人的失误造成 “A 比 B 重要，B 比 C 重要，C 比 A 重要” 的错误判别情形。我们可以通过一致性检验来判断是否出现了这样的情况。

如果矩阵没有通过一致性检验，那么就要重新构造矩阵，并检查在构造矩阵时有没有逻辑错误；如果矩阵通过了一致性检验，那么我们就可以继续通过算术方法求解层次分析。（实际上这里还有另外一种基于矩阵的特征值和特征向量的方法，但我们这里就采取最简单的算术方法。）

我们需要计算权重向量。权重计算的方法是：

1. 对矩阵进行过优化，这要求将矩阵的每一列相加，然后将这一列的所有元素，除以这一列所有元素相加的和。对矩阵的所有列都进行这样的操作，就能将矩阵归一化。
2. 将归一化之后的矩阵每一行相加，得到一个加和。然后用这个加和去除以矩阵的行数或者列数（因为矩阵是方形的，所以行数就等于列数）。这会产生出一个权重向量。
3. 将方案矩阵所产生的权重向量中的每一个数字，分别乘以准则矩阵产生的权重向量中的每一个数字。

注意：这里不是要将两个向量相乘，而是用向量乘以数字。打个比方说，我们这里有 C1、C2、C3 这三个矩阵，我们假设每一个巨人都产生了一个包含五个元素的权重向量；而在准则层有准则矩阵 C，产生了包含三个元素的权重向量。这个时候我们就要拿 C1 权重向量里的每一个数字都乘以 C 产生的权重向量里的第一个元素；C2 权重向量里的每一个数字都乘以 C 产生的权重向量里的第二个元素；C3 权重向量里的每一个数字都乘以 C 产生的权重向量里的第三个元素

我们把我们刚才写出来的两级矩阵都写入 Python，保存为 numpy.array() 格式。

首先是准则矩阵：

criteria = np.array(
    [ 
        [ 1, 1/5, 1/3 ],
        [ 5,   1,   3 ],
        [ 3, 1/3,   1 ] 
        ] 
    )

接下来针对每个教师写出相应的方案矩阵：

# 第二级矩阵
C1 = np.array(
    [ 
        [	   1, 	   2, 	   5, 	   4, 	7   ], 
	    [	 1/2,	   1, 	   3, 	   2, 	5   ], 
	    [	 1/5,	 1/3,	   1, 	 1/2,	2   ], 
	    [	 1/4,	 1/2,	   2, 	   1, 	3   ], 
	    [	 1/7,	 1/5,	 1/2,	 1/3,	1   ], 
        ]
    )
C2 = np.array(
	[ 
		[	   1, 	 1/7, 	 2/3, 	 1/5 	], 
	    [	   7,	   1, 	   5, 	   2 	], 
	    [	   3,	 1/5,	   1, 	 1/3	], 
	    [	   5,	 1/2,	   3, 	   1 	], 
		] 
	)
C3 = np.array(
    [ 
        [	   1, 	   1, 	   3, 	   3 	], 
	    [	   1,	   1, 	   3, 	   3 	], 
	    [	 1/3,	 1/3,	   1, 	   1	], 
	    [	 1/3,	 1/3,	   1, 	   1 	], 
        ] 
    )

可以看见这里矩阵 C2 和 C3 都只有四行四列。造成的结果就是我们后续在计算矩阵的权重向量的时候，这两个矩阵的权重向量会只有四个元素。我在这里的解决办法是给这两个矩阵的权重向量添加一个元素 0。我觉得这样既能够避免在进行矩阵归一化的时候出现除以零的操作，也保证了权重计算不会受到影响。（可能还有更好的解决方案，但我没想到。）

层次分析法的代码实现

一致性检验的基本步骤

1. 计算特征向量（Eigenvector）：使用判断矩阵计算特征向量，表示每个因素相对于其他因素的重要性。这可以通过计算判断矩阵的最大特征值和对应的特征向量来实现。

2. 计算一致性指标（Consistency Index）：根据特征向量计算一致性指标以评估决策者所提供的数据是否具有一致性。一致性指标通过以下公式计算：

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

其中，${\lambda }_{max}$ 是判断矩阵的最大特征值，$n$ 是判断矩阵的维度（即因素的数量）。

3. 计算随机一致性指标（Random Index）：为了将一致性指标与随机一致性进行比较，需要使用随机一致性指标。随机一致性指标是根据判断矩阵的维度计算得出的。

4. 计算一致性比率（Consistency Ratio）：通过将一致性指标除以随机一致性指标，可以计算出一致性比率，用于评估判断矩阵的一致性。一致性比率的计算公式如下：

$$CR=\frac{CI}{RI}$$

其中，$RI$ 是对应于判断矩阵维度的随机一致性指标。不同阶数的矩阵对应的 RI 如下表所示：

阶数 n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
RI	0	0	0.58	0.9	1.12	1.24	1.32	1.41	1.45	1.49	1.52	1.54	1.56	1.58	1.59

5. 判断一致性：根据给定的判断矩阵和计算得到的一致性比率，可以参考以下常用的判断标准来评估一致性：

• 如果 $CR<0.1$，则认为判断矩阵具有可接受的一致性；
• 如果 $0.1\le CR<0.2$，则认为判断矩阵具有可接受的但不太理想的一致性；
• 如果 $CR\ge 0.2$，则认为判断矩阵具有不可接受的一致性。

如果判断矩阵不满足一致性标准，可能需要重新审查和调整判断矩阵，以提高一致性。

这里代码参考了这篇文章：层次分析法之python，我们定义一个函数用于对各个矩阵进行一致性检验。

def consistence_test( M, name = "" ):
    RI=[ 0,    0,    0.58, 0.9,  1.12, 
         1.24, 1.32, 1.41, 1.45, 1.49, 
         1.52, 1.54, 1.56, 1.58, 1.59 ]
    [n, n] = M.shape # 判别矩阵为方阵，只用 n 接收参数即可
    V, D = np.linalg.eig(M)
    max_eig_value = np.max(V)
    CI = ( max_eig_value - n ) / ( n-1 )
    CR = CI / RI[n-1]
    if CR >= 0.1: #判断是否通过一致性检验
        print( name, '没有通过一致性检验')
    else:
        print( name, '成功通过一致性检验')

对每一个判别矩阵的一致性检验结果如下。 可以看到，我们构建的矩阵都通过了检验。实际上这些矩阵都是提干条件给出的，出于题目合理性的考量，理论上都能够通过检验。

假如在这里出现了矩阵没有通过一致性检验的情况，我们就需要重新构建判别矩阵

consistence_test( criteria, "准则矩阵" )
consistence_test( C1, "C1" )
consistence_test( C2, "C2" )
consistence_test( C3, "C3" )

准则矩阵 成功通过一致性检验
C1 成功通过一致性检验
C2 成功通过一致性检验
C3 成功通过一致性检验

由于三个矩阵都通过了一致性检验，我们这里就可以进行层次分析法的操作。我们定义一个函数来计算矩阵的权重向量，这里参考了博文 数学建模–层次分析法（代码Python实现）

def aph_matix_weight( M, name = "" ): 
    # 将判断矩阵按照列归一化（每个元素除以其所在列的和）
    sum_M = M.sum(axis=0)  #计算X每列的和
    ( n, n ) = M.shape  #X为方阵，行和列相同，所以用一个 n 来接收
    sum_M = np.tile( sum_M, (n, 1) )  #将和向量重复 n 行组成新的矩阵
    stand_M = M/sum_M  #标准化 X（ X 中每个元素除以其所在列的和）
    
    # 将归一化矩阵每一行求和
    sum_row = stand_M.sum( axis = 1 )

    # 将相加后得到的向量中每个元素除以n即可得到权重向量
    print( name, "权重：", sum_row / n )
    return sum_row / n

权重向量的计算结果如下：

criteria_weights = aph_matix_weight( criteria, "准则矩阵" )
C1_weights = aph_matix_weight( C1, "C1" )
C2_weights = aph_matix_weight( C2, "C2" )
C3_weights = aph_matix_weight( C3, "C3" )

准则矩阵 权重： [0.10615632 0.63334572 0.26049796]
C1 权重： [0.46159865 0.25616165 0.08802104 0.14233203 0.05188663]
C2 权重： [0.06639717 0.51585369 0.12345376 0.29429538]
C3 权重： [0.375 0.375 0.125 0.125]

矩阵 C1 和 C3 都只有四行四列。我们在这里手动为权重向量添加 0 元素：

C2_weights = np.insert(C2_weights, 0, 0)
C3_weights = np.append(C3_weights, 0 )
print( C2_weights, C3_weights )

[0.         0.06639717 0.51585369 0.12345376 0.29429538] [0.375 0.375 0.125 0.125 0.   ]

将方案矩阵所产生的权重向量中的每一个数字，分别乘以准则矩阵产生的权重向量中的每一个数字（具体过程在上面说过）

C1_score = C1_weights * criteria_weights[0]
C2_score = C2_weights * criteria_weights[1]
C3_score = C3_weights * criteria_weights[2]
print(C1_score)
print(C2_score)
print(C3_score)

[0.04900162 0.02719318 0.00934399 0.01510945 0.00550809]
[0.         0.04205236 0.32671373 0.07818891 0.18639072]
[0.09768673 0.09768673 0.03256224 0.03256224 0.        ]

最后把这些数值加起来，就是各个教师的最终评分。

P1_score = C1_score[0] + C2_score[0] + C3_score[0]
P2_score = C1_score[1] + C2_score[1] + C3_score[1]
P3_score = C1_score[2] + C2_score[2] + C3_score[2]
P4_score = C1_score[3] + C2_score[3] + C3_score[3]
P5_score = C1_score[4] + C2_score[4] + C3_score[4]

输出层次分析结果：

print("P1 权重打分", P1_score)
print("P2 权重打分", P2_score)
print("P3 权重打分", P3_score)
print("P4 权重打分", P4_score)
print("P5 权重打分", P5_score)

P1 权重打分 0.14668834948594095
P2 权重打分 0.16693227402847738
P3 权重打分 0.36861996335974256
P4 权重打分 0.12586059859545307
P5 权重打分 0.19189881453038599

根据层次分析法的最终结果判断，教师 P3 为优秀教师