【二叉树】练习题终章
二叉树的销毁
void BTreeDestroy(BTNode* root)
{
if (root == NULL)
return;
BTreeDestroy(root->left);
BTreeDestroy(root->right);
free(root);
}
递归展示图
使用后序销毁,如果用前序销毁的话,就会找不到根对应的子树的地址.下面就不能被销毁了,所以从子树开始销毁,自下而上的销毁方式,采用后序.
二叉树的遍历
代码实现
#include 思路分析:
我们可以根据给定的字符串进行还原二叉树,按照先序遍历,所以还原出来为下图的样子
因为要输入一段字符串,从字符串中读取到二叉树中,对应的操作为
char a[100];
scanf("%s",a);
由于要构建二叉树,先构建一个二叉树节点的结构体
typedef struct BinaryTreeNode {
char data;//节点数据
struct BinaryTreeNode* left;//左子树结点地址
struct BinaryTreeNode* right;//右子树结点地址
} BTNode;
定义一个创建二叉树的函数
BTNode* BinaryTreeCreate(char*a,int*pi)
函数的返回值为树节点的地址,参数分别为要构建二叉树的字符串,第二个参数是传递构建字符串数组的下标,为了防止栈销毁时,参数被销毁,所以传下标的地址过去,下标从0开始.
如果a字符串的第一个元素开始构建二叉树,当遇到‘#’,相当与构建二叉树的NULL,return NULL即可,并且a数组下标加到下一个元素,当遇到一个非‘#’时,malloc一个树的结点,地址保存在root里面,root->data=a[(*pi)++];将数据写进该节点,(*pi)++表示赋值后,下标指向下一个元素,递归调用左子树和右子树,同理创建子树,然后返回创建好根的地址,然后通过中序遍历打印即可.
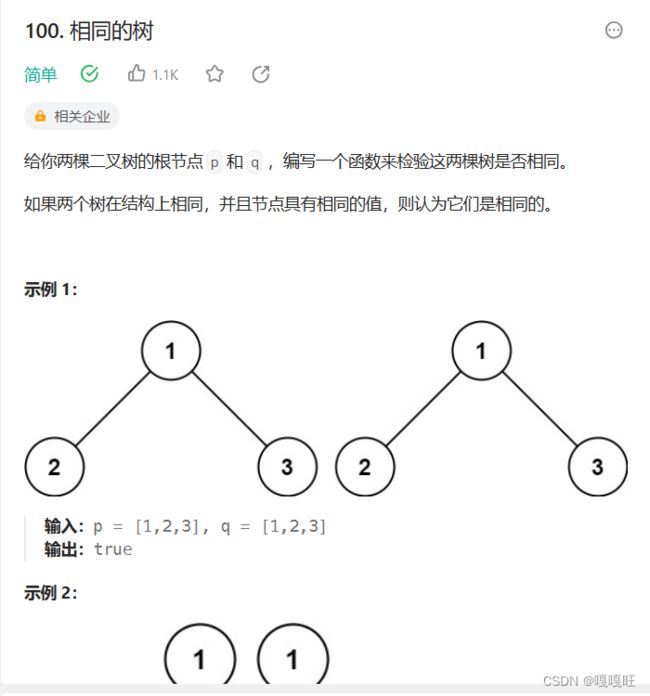
相同的树
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if(p==NULL&&q==NULL)
return true;
if(p==NULL||q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
代码分析:当两个树为空树时,两个为相同的树,返回true,当程序经过这个判断条件,并且没有结束,说明两颗树不同时为空 ,如果一个树为空,另一个树不为空,则两颗树不相等,返回false;
如果程序还没有结束,则说明两个树的该节点都不为空,判断两个节点存在后,如果两个节点不相等,则返回false,如果程序还没有结束,则说明两颗树的根节点相等,接下来递归判断左子树和右子树,因为要判断的是两颗树是否相同,则必须保证制左子树相同且右子树相同,二者是&&的关系。
翻转二叉树
struct TreeNode* invertTree(struct TreeNode* root) {
if(root==NULL)
return NULL ;
struct TreeNode* left=invertTree(root->left);
struct TreeNode* right=invertTree(root->right);
root->left=right;
root->right=left;
return root;
}
递归遍历图

根据递归图我们可以看到,先发生交换的是两个空节点,然后进行,1,3的交换,然后是6和9的交换.
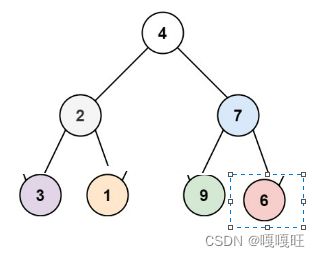
交换后如上图所示.
然后就是2,7的交换
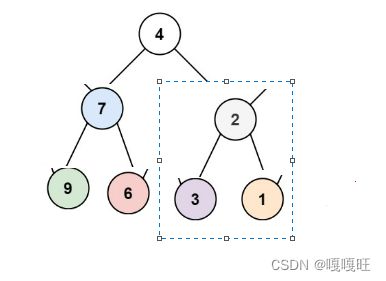
注意:本质上是根节点的左右子树地址的交换.
二叉树的层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历.

层序遍历的接口
// 层序遍历
void LevelOrder(BTNode* root);
实现方法:使用队列这种结构,当队列中没有数据时,我们可以先入队列一个堆顶数据,这里着重强调入队的元素为树节点的地址,然后队列不为空.先保存队列中元素的地址,然后出队列,并且打印这个出队列的元素,由于已经保存好堆顶节点的地址,所以我们可以找到对应的子树,当出一个根节点时,如果根节点的左右子树不为空地话,就将左右子树节点的地址入队列,总结是,先入队列一个,当这个元素出队列时,依次入队列他的左子树和右子树的地址,在出这个左子树时,同理,将他的左右子树依次入队列.
图片演示

代码展示
首先是队列的功能函数
typedef struct QListNode
{
struct QListNode* next;//保存结点的下一个结点的地址
int data;//该节点的数据
}QNode;
typedef struct Queue
{
QNode* front;
QNode* tail;
}Queue;//定义一个队列结构体,指向队列的前结点和尾结点
// 初始化队列
void QueueInit(Queue* q)
{
assert(q);
q->front = q->tail = NULL;//头节点尾结点置为NULL
}
// 队尾入队列
void QueuePush(Queue* q, int data)
{
assert(q);
QNode* newnode = (QNode*)malloc(sizeof(QNode));//新结点申请空间
assert(newnode);//防止申请失败
newnode->next = NULL;//新节点的下一个结点的地址为空,不保存
newnode->data = data;//新结点的数据
if (q->front == NULL)//没有一个结点
{
q->front = q->tail = newnode;//就让指向头节点和指向尾结点的指针指向新结点
}
else//有结点
{
q->tail->next = newnode;//新结点尾插到后面
q->tail = newnode;//移动指向尾结点的指针到队列末尾结点,也就是新结点
}
}
// 检测队列是否为空,如果为空返回非零结果,如果非空返回0
int QueueEmpty(Queue* q)
{
return q->front == NULL;//如果没有结点,则q->front==NULL,表达式成立返回1,表明队列为空
}
// 队头出队列
void QueuePop(Queue* q)
{
assert(q);
assert(!QueueEmpty(q));//防止队列为空在出数据
if (q->front->next == NULL)//如果只有一个结点
{
q->front = q->tail == NULL;//那就把这个结点置空,指向头结点指针和指向尾结点的指针指向空
}
else
{
QNode* next = q->front->next;//保存下一个结点的地址
free(q->front);//从头结点开始释放一个结点,也就是头删
q->front = next;//指向头结点的指针移动到下一个位置
}
}
// 获取队列头部元素
int QueueFront(Queue* q)
{
assert(q);
assert(q->front);//防止头节点为空
return q->front->data;//头结点数据
}
// 获取队列队尾元素
int QueueBack(Queue* q)
{
assert(q);
assert(q->tail);//防止尾节点为空
return q->tail->data;//尾节点数据
}
// 获取队列中有效元素个数
int QueueSize(Queue* q)
{
int size = 0;//记录元素个数变量
assert(q);
QNode* cur = q->front;//遍历队列的指针先指向头
while (cur)
{
size++;//遍历记数
cur = cur->next;
}
return size;//返回有效数据个数
}
// 销毁队列
void QueueDestroy(Queue* q)
{
assert(q);
QNode* cur = q->front;//遍历队列的指针
while (cur)
{
QNode* next = cur->next;//保存下一个节点的地址
free(cur);//释放掉当前cur指针指向当前位置的空间
cur = next;//指向下一个位置
}
q->front = q->tail = NULL;//防止野指针
}
层序遍历实现
void LevelOrder(BTNode* root)
{
Queue sk;
QueueInit(&sk);
if (root != NULL)
{
QueuePush(&sk,root);
}
while (!QueueEmpty(&sk))
{
BTNode* front=QueueFront(&sk);
QueuePop(&sk);
printf("%d ", front->data);
if (front->left != NULL)
{
QueuePush(&sk, front->left);
}
if (front->right != NULL)
{
QueuePush(&sk, front->right);
}
}
QueueDestroy(&sk);
}
包含的头文件
#include 判断二叉树是否为完全二叉树
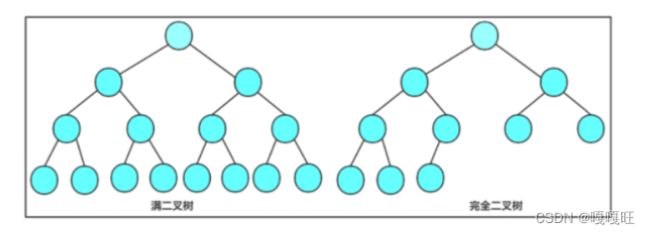
方法:层序遍历二叉树,会出现数据都是连续的.

如果是这样的,则他不是完全二叉树。
如何实现,用到了层序遍历,我们当队列没数据时,先入一个堆顶节点进去,和层序遍历一样,不同的是,如果队前元素为空地话会退出判断队列为空的循环,此时检查队列种如果有非空元素,则说明该树不是完全二叉树
图示说明:

比如说这个例子:

如果修改一下:

代码展示
bool BTreeComplete(BTNode* root)
{
Queue sk;
QueueInit(&sk);
if (root != NULL)
{
QueuePush(&sk, root);
}
while (!QueueEmpty(&sk))
{
BTNode* front= QueueFront(&sk);
QueuePop(&sk);
if (front == NULL)
{
break;
}
QueuePush(&sk, front->left);
QueuePush(&sk, front->right);
}
while (!QueueEmpty(&sk))
{
BTNode* front = QueueFront(&sk);
QueuePop(&sk);
if (front != NULL)
{
QueueDestroy(&sk);
return false;
}
}
QueueDestroy(&sk);
return true;
}
注意这里入队列的还是二叉树节点的地址,为了方便展示,上图演示我用的是元素。