基于遗传算法求函数最大值
首先说一下作业题目:
设定求解精确到2位小数,种群规模: 50,最大进化代数: 150,交叉概率: Pc=0.25,变异概率: Pm=0.01 。
本次算法编程思想来源于http://t.csdn.cn/7wsRq。主要是理解遗传算法的设计过程。遗传算法的进化过程类似一个物种的进化过程,寻找函数最大值的过程就是寻找种群中的最优个体的过程。本题使用二进制位串编码方式,位串模拟自然界中的染色体,位串中的每一位模拟自然界中的基因,如长度为9的位串111001010代表一条染色体,其1或0代表该染色体上的基因位。选择、交叉、变异操作就是建立在基因和染色上的。
接下来进入正题:
(1)首先是进行数据准备:
根据题目要求设置初始种群大小为NP=50,即含有50个个体或50条染色体。最大迭代次数G=150选取位串长度为L=9(位串长度和精度有关),即每条染色体的基因个数。变异概率Pm=0.01,则对于该种群总共有NP×Pm=50×0.01=0.5条染色体可能发生变异,对于每条染色体总共有L×Pm=9×0.01=0.09个基因可能发生变异,即该种群没有染色体发生变异,这可能会降低种群进化的多样性,导致无法获取全局最优解,后面会说到这个问题。
(2)选择:采用随机的方法获取初始种群,再采用轮盘赌的方法选择优良个体,过程如下:
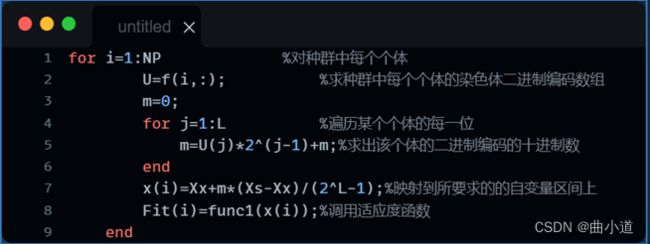
首先,将每个染色体的二进制转换为十进制数m,再将m映射到自变量区间[-1,2]上,然后将目标函数作为适应度函数,求出该染色体的适应度值,重复操作求出上一代种群每个个体的适应度值;
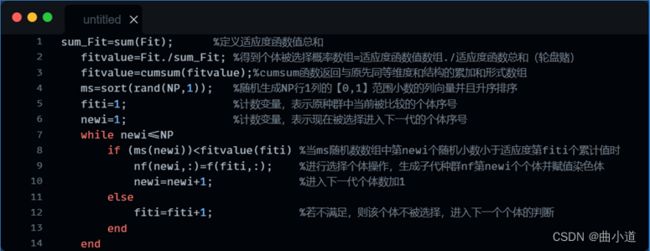
接着,先对适应度值进行归一化处理(防止适应度值之间相差过大导致物种多样性的降低),再对群体的适应度值求和,然后分别求出每个染色体的适应度值比例,即被选择的概率。为了编程方便,将选择概率逐个累加起来,比如染色体1的选择概率为P1=0.12,染色体2的选择概率P2=0.13,依次P3=0.14,则P1=P1=0.12,P2=P1+P2=0.25,P3=P1+P2=0.25+0.14=0.39,依次进行。
然后,随机生成NP行1列的(0,1)范围内的随机数组ms模拟旋转概率,并按升序的方式排列。
再然后,保留被选择下来的新一代染色体nf,保留方式为:当ms随机数数组中第newi个随机小数小于适应度第fiti个累计值时,保留该染色体,否则,淘汰该染色体,进入下一个染色体的选择。
最后,重复选择操作,得出新一代染色体。
其映射方式如下:
x=Xx+m*(Xs-Xx)/(2^L-1)
其中,Xx=-1,表示自变量范围的下限;Xs=2,表示自变量范围的上限;m,表示二进制位串的十进制转换数值;L=9,表示二进制位串长度。
转换十进制和映射代码如下:
(3)交叉
第一步是将选择产生的匹配池中的成员随机两两匹配;第二步是进行交叉繁殖,具体过程如下:首先,随机生成一个(0,1)之间的小数p;然后,将其与交叉概率Pc比较,若p
(4)变异
由于本题没有变异串位,故省去此操作。但观察结果会发现,没有变异的进化降低了种群多样性,导致过早收敛。而在提升了变异概率之后(例如设变异概率为0.1),种群能得到全局收敛的结果。这里简述一下变异过程如下:首先,得到需要变异的染色体数NP*Pm=0.1*50=5;然后,随机选择一条需要变异的染色体,并计算需要变异的染色总共进行变异的基因位L*Pm=10*0.1=1;然后,再随机选取需要变异的基因序号,并对该基因位取反;最后,重复操作直到所有需变异的染色体中待变异的基因位完后变异得到新一代种群为止。
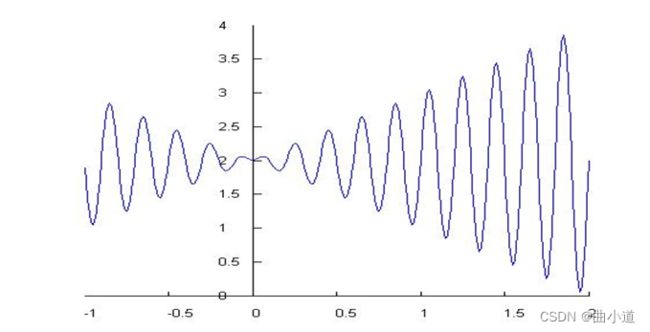
结果如下:首先,我们将目标函数的图像绘制出来并得到目标函数的最大值为3.8500。
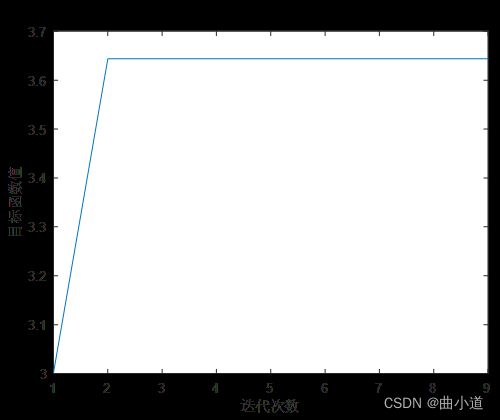
然后,按照题目要求,设置变异率为0.01,得出的最大值点为(1.65,3.64),可见与实际最大值3.85有误差,这是由于变异率过低,丧失了变异功能,使多样性下降,导致收敛到局部极值的效果,该迭代次数只进行到第9次,其图示结果如下:
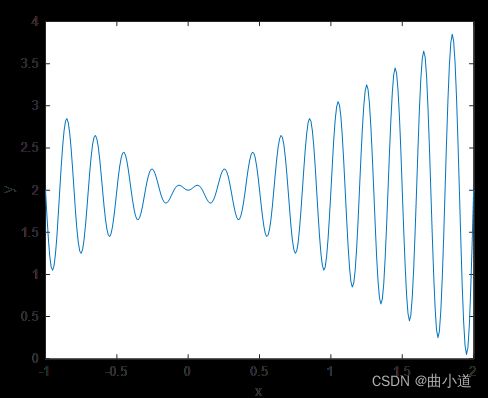
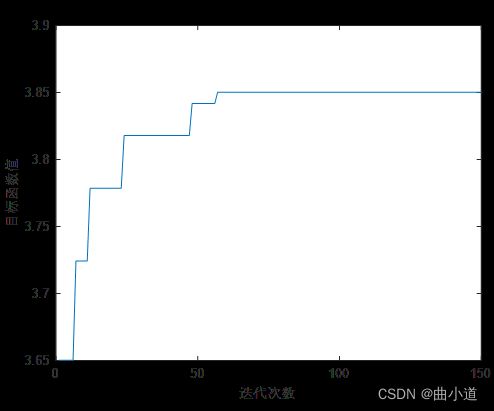
最后,改变变异概率并令Pm=0.1后,得到的函数最大值点为(1.85,3.85),实际目标函数最大值为3.8500,这里我们发现,当设置位串长度为L=9时,得到的最大值点为(1.8532,3.8437),相比较位串长度为L=10时,误差更大。这是由于位串长度在一定范围内越大,插值点越密,所得到的结果精度越高,当位串长度达到一定值后再增加,提高精度的效果微乎其微,但是会增加计算的复杂性,降低计算效率,因此,在满足精度要求下尽可能取小的L最合适,本题在多次调整参数L下,得到当L=10时是最合适的二进制位串长度。
L=10的结果
L=9的结果
程序代码:
改变变异概率后,加入的变异部分代码如下(将该部分代码放入题目代码中的57-58行之间即可):
新手上路,思考了很久,决定通过平台的分享来提升自己思维的严密性,方便以后查阅,由于刚开始写,难免有不足之处,欢迎批评指正。