数据科学必备分布
正态分布
正态分布(Normal distribution),也被称为高斯分布(Gaussian distribution),是概率论和统计学中非常重要的一种概率分布。
正态分布的特点是呈钟形曲线,并且在均值处具有对称性。其概率密度函数(Probability Density Function,简称PDF)可以用以下数学公式表示:其中,μ表示均值(即钟形曲线的中心),σ表示标准差(决定曲线的宽度和形状)
公式
from scipy.stats import norm
import matplotlib.pyplot as plt
# 生成正态分布数据
mu = 0 # 均值
sigma = 1 # 标准差
data = norm.rvs(mu, sigma, size=1000) # 生成1000个符合正态分布的随机数
# 绘制直方图
plt.hist(data, bins=30, density=True, alpha=0.7, color='blue')
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Normal Distribution')
plt.show()
正态分布概述
正态分布随机变量的赋范概率密度函数(pdf)和累积密度函数(cdf)
# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)
# PDF 概率密度
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100)) / np.max(stats.norm.pdf(np.linspace(-3, 3, 100))),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100)) / np.max(stats.norm.pdf(np.linspace(-3, 3, 100))),
alpha=.15,
)
# CDF 累计概率密度
plt.plot(np.linspace(-4, 4, 100),
stats.norm.cdf(np.linspace(-4, 4, 100)),
)
# LEGEND
plt.text(x=-1.5, y=.7, s="pdf (normed)", rotation=65, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=-.4, y=.5, s="cdf", rotation=55, alpha=.75, weight="bold", color="#fc4f30")
# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE
plt.text(x = -5, y = 1.25, s = "Normal Distribution - Overview",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -5, y = 1.1,
s = 'Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a normally distributed random variable $ y \sim \mathcal{N}(\mu,\sigma) $, given $ \mu = 0 $ and $ \sigma = 1$.',
fontsize = 19, alpha = .85)均值对正态分布图像的影响
plt.figure(dpi=100)
# PDF MU = 0
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100)),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100)),
alpha=.15,
)
# PDF MU = 2 均值为2
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), loc=2),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100),loc=2),
alpha=.15,
)
# PDF MU = -2 均值为-2
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), loc=-2),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100),loc=-2),
alpha=.15,
)
# LEGEND
plt.text(x=-1, y=.35, s="$ \mu = 0$", rotation=65, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=1, y=.35, s="$ \mu = 2$", rotation=65, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=-3, y=.35, s="$ \mu = -2$", rotation=65, alpha=.75, weight="bold", color="#e5ae38")
# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE,
plt.text(x = -5, y = 0.51, s = "Normal Distribution - $ \mu $",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -5, y = 0.45,
s = 'Depicted below are three normally distributed random variables with varying $ \mu $. As one can easily\nsee the parameter $\mu$ shifts the distribution along the x-axis.',
fontsize = 19, alpha = .85)标准差对正态分布图像的影响
plt.figure(dpi=100)
# PDF SIGMA = 1
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), scale=1),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), scale=1),
alpha=.15,
)
# PDF SIGMA = 2
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), scale=2),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), scale=2),
alpha=.15,
)
# PDF SIGMA = 0.5
plt.plot(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), scale=0.5),
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.norm.pdf(np.linspace(-4, 4, 100), scale=0.5),
alpha=.15,
)
# LEGEND
plt.text(x=-1.25, y=.3, s="$ \sigma = 1$", rotation=51, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=-2.5, y=.13, s="$ \sigma = 2$", rotation=11, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=-0.75, y=.55, s="$ \sigma = 0.5$", rotation=75, alpha=.75, weight="bold", color="#e5ae38")
# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE, SUBTITLE & FOOTER
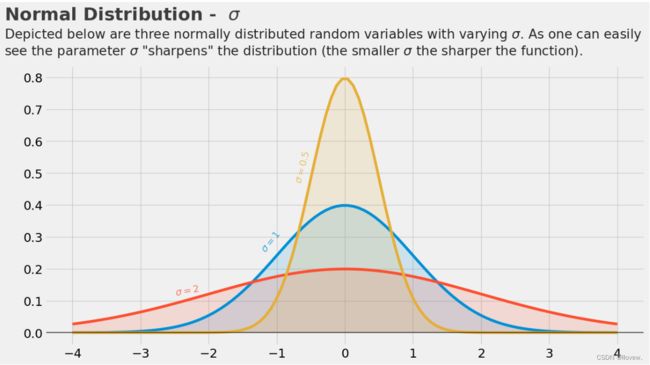
plt.text(x = -5, y = 0.98, s = "Normal Distribution - $ \sigma $",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -5, y = 0.87,
s = 'Depicted below are three normally distributed random variables with varying $\sigma $. As one can easily\nsee the parameter $\sigma$ "sharpens" the distribution (the smaller $ \sigma $ the sharper the function).',
fontsize = 19, alpha = .85)基于数据画出分布
##### COMPUTATION #####
# DECLARING THE "TRUE" PARAMETERS UNDERLYING THE SAMPLE
mu_real = 10
sigma_real = 2
# DRAW A SAMPLE OF N=1000
np.random.seed(42)
sample = stats.norm.rvs(loc=mu_real, scale=sigma_real, size=1000)
# ESTIMATE MU AND SIGMA
mu_est = np.mean(sample)
sigma_est = np.std(sample)
print("Estimated MU: {}\nEstimated SIGMA: {}".format(mu_est, sigma_est))
##### PLOTTING #####
# SAMPLE DISTRIBUTION
plt.hist(sample, bins=50,normed=True, alpha=.25)
# TRUE CURVE
plt.plot(np.linspace(2, 18, 1000), norm.pdf(np.linspace(2, 18, 1000),loc=mu_real, scale=sigma_real))
# ESTIMATED CURVE
plt.plot(np.linspace(2, 18, 1000), norm.pdf(np.linspace(2, 18, 1000),loc=np.mean(sample), scale=np.std(sample)))
# LEGEND
plt.text(x=9.5, y=.1, s="sample", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=7, y=.2, s="true distrubtion", rotation=55, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=5, y=.12, s="estimated distribution", rotation=55, alpha=.75, weight="bold", color="#e5ae38")
# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE
plt.text(x = 0, y = 0.3, s = "Normal Distribution",
fontsize = 26, weight = 'bold', alpha = .75)二项式分布
二项式分布就是只有两个可能结果的分布,比如成功或失败、得到或者丢失、赢或败,每一次尝试成功和失败的概率相等。
每一次尝试都是独立的,因为前一次投掷的结果不能决定或影响当前投掷的结果。只有两个可能的结果并且重复n次的实验叫做二项式。二项分布的参数是n和p,其中n是试验的总数,p是每次试验成功的概率。
二项式分布的属性包括:
- 每个试验都是独立的。
- 在试验中只有两个可能的结果:成功或失败。
- 总共进行了n次相同的试验。
- 所有试验成功和失败的概率是相同的。 (试验是一样的)
公式
-
PMF( 概率质量函数 ): 是对 离散随机变量 的定义. 是 离散随机变量 在各个特定取值的概率. 该函数通俗来说,就是 对于一个离散型概率事件来说, 使用这个函数来求它的各个成功事件结果的概率.
-
PDF ( 概率密度函数 ): 是对 连续性随机变量 的定义. 与PMF不同的是 PDF 在特定点上的值并不是该点的概率, 连续随机概率事件只能求一段区域内发生事件的概率, 通过对这段区间进行积分来求. 通俗来说, 使用这个概率密度函数 将 想要求概率的区间的临界点( 最大值和最小值)带入求积分.,就是该区间的概率。
python实现二项式分布实例
我们假设进行10次试验(n=10),每次试验成功的概率为0.5(p=0.5)。通过 binom.pmf() 函数,我们可以计算出每个成功次数的概率质量。
from scipy.stats import binom
# 二项式分布参数
n = 10 # 试验次数
p = 0.5 # 成功的概率
# 计算概率质量函数
x = range(0, n+1) # 成功次数的取值范围
pmf = binom.pmf(x, n, p) # 计算每个取值的概率质量
# 打印结果
for i in range(len(x)):
print(f"成功次数为 {x[i]} 的概率为 {pmf[i]}")
# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)
# PDF
plt.bar(left=np.arange(20),
height=(stats.binom.pmf(np.arange(20), p=.5, n=20)),
width=.75,
alpha=0.75
)
# CDF
plt.plot(np.arange(20),
stats.binom.cdf(np.arange(20), p=.5, n=20),
color="#fc4f30",
)
# LEGEND
plt.text(x=4.5, y=.7, s="pmf (normed)", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=14.5, y=.9, s="cdf", alpha=.75, weight="bold", color="#fc4f30")
# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0.005, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE, SUBTITLE & FOOTER
plt.text(x = -2.5, y = 1.25, s = "Binomial Distribution - Overview",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -2.5, y = 1.1,
s = 'Depicted below are the normed probability mass function (pmf) and the cumulative density\nfunction (cdf) of a Binomial distributed random variable $ y \sim Binom(N, p) $, given $ N = 20$ and $p =0.5 $.',
fontsize = 19, alpha = .85)P对结果的影响
plt.figure(dpi=100)
# PDF P = .2
plt.scatter(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.2, n=20)),
alpha=0.75,
s=100
)
plt.plot(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.2, n=20)),
alpha=0.75,
)
# PDF P = .5
plt.scatter(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.5, n=20)),
alpha=0.75,
s=100
)
plt.plot(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.5, n=20)),
alpha=0.75,
)
# PDF P = .9
plt.scatter(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.9, n=20)),
alpha=0.75,
s=100
)
plt.plot(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.9, n=20)),
alpha=0.75,
)
# LEGEND
plt.text(x=3.5, y=.075, s="$p = 0.2$", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=9.5, y=.075, s="$p = 0.5$", alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=17.5, y=.075, s="$p = 0.9$", alpha=.75, weight="bold", color="#e5ae38")
# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE, SUBTITLE & FOOTER
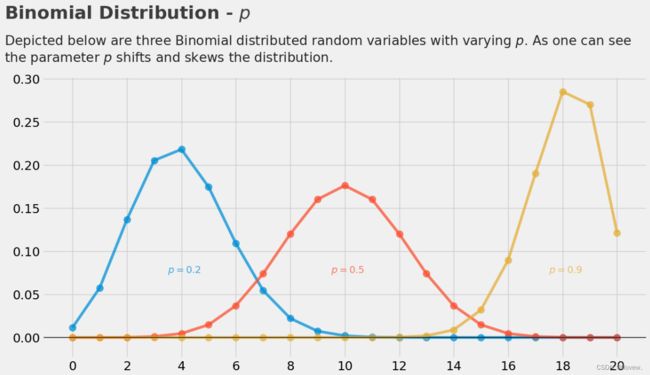
plt.text(x = -2.5, y = .37, s = "Binomial Distribution - $p$",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -2.5, y = .32,
s = 'Depicted below are three Binomial distributed random variables with varying $p $. As one can see\nthe parameter $p$ shifts and skews the distribution.',
fontsize = 19, alpha = .85)N对结果的影响
plt.figure(dpi=100)
# PDF N = 10
plt.scatter(np.arange(11),
(stats.binom.pmf(np.arange(11), p=.5, n=10)),
alpha=0.75,
s=100
)
plt.plot(np.arange(11),
(stats.binom.pmf(np.arange(11), p=.5, n=10)),
alpha=0.75,
)
# PDF N = 15
plt.scatter(np.arange(16),
(stats.binom.pmf(np.arange(16), p=.5, n=15)),
alpha=0.75,
s=100
)
plt.plot(np.arange(16),
(stats.binom.pmf(np.arange(16), p=.5, n=15)),
alpha=0.75,
)
# PDF N = 20
plt.scatter(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.5, n=20)),
alpha=0.75,
s=100
)
plt.plot(np.arange(21),
(stats.binom.pmf(np.arange(21), p=.5, n=20)),
alpha=0.75,
)
# LEGEND
plt.text(x=6, y=.225, s="$N = 10$", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=8.5, y=.2, s="$N = 15$", alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=11, y=.175, s="$N = 20$", alpha=.75, weight="bold", color="#e5ae38")
# TICKS
plt.xticks(range(21)[::2])
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE, SUBTITLE & FOOTER
plt.text(x = -2.5, y = .31, s = "Binomial Distribution - $N$",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -2.5, y = .27,
s = 'Depicted below are three Binomial distributed random variables with varying $N$. As one can see\nthe parameter $N$ streches the distribution (the larger $N$ the flatter the distribution).',
fontsize = 19, alpha = .85)泊松分布
泊松分布是用于描述在特定时间或空间间隔内某事件发生的次数的概率分布。它适用于事件发生的概率很低,并且相互独立(一个事件的发生不会影响其他事件发生)的情况。
公式
泊松分布由一个参数λ(lambda)来描述,表示在给定时间或空间间隔内平均发生的事件次数。泊松分布的概率质量函数可以表示为:
其中,k表示我们关心的事件发生的次数,e是自然对数的底数(约等于2.71828)。
泊松分布具有以下特征:
- 平均发生的事件次数λ相对较小,但可能无限大。
- 事件之间是相互独立的。
- 事件只能在离散时间或空间点上发生,不会发生在连续的时间或空间区间上。
泊松分布的应用:
- 模拟随机事件的发生,如电话呼叫的数量、到达交通信号灯的车辆数量等。
- 在保险数学中,用于建模和估计在特定时间段内发生的事故数量。
- 在生物统计学中,用于记录某种疾病在特定区域内的发生率。
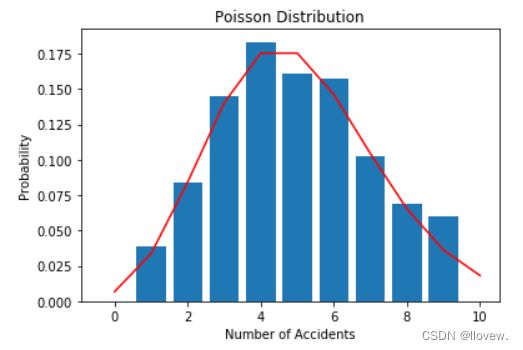
使用泊松分布的模型来模拟交通事故数量
当我们需要描述在给定时间或空间单位内事件发生的次数时,泊松分布是一种常用的概率分布模型。它常用于模拟稀有事件的发生概率,比如在一段时间内发生的交通事故数量、电话呼叫数量等等。假设我们正在研究某个城市在一天内的交通事故数量。我们知道该城市平均每天发生5起交通事故,现在我们希望使用泊松分布来建模这种情况。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# 设置平均交通事故数量
average_accidents = 5
# 生成泊松分布的随机数
accidents = np.random.poisson(average_accidents, 1000)
# 绘制直方图
plt.hist(accidents, bins=range(0, 11), align='left', rwidth=0.8, density=True)
# 绘制泊松分布的概率质量函数
x = np.arange(0, 11)
y = poisson.pmf(x, average_accidents)
plt.plot(x, y, 'r')
plt.xlabel('Number of Accidents')
plt.ylabel('Probability')
plt.title('Poisson Distribution')
plt.show()
均匀分布
对于投骰子来说,结果是1到6。得到任何一个结果的概率是相等的,这就是均匀分布的基础。与伯努利分布不同,均匀分布的所有可能结果的n个数也是相等的。
公式
如果变量X是均匀分布的,则密度函数可以表示为:
使用均匀分布建模实例
假设我们要模拟一次掷骰子的结果。我们可以使用均匀分布来表示骰子的每个面出现的概率。
在这个例子中,假设我们有一个六面骰子,每个面上的数字分别为1、2、3、4、5和6。我们可以使用均匀分布将概率平均地分配给这六个可能的结果。
首先,我们需要确定概率分布的定义域。在这个例子中,定义域是骰子的可能结果,即[1, 2, 3, 4, 5, 6]。
接下来,我们可以使用概率密度函数来定义均匀分布。由于每个结果都有相同的概率,因此概率密度函数为 f(x) = 1 / 6,其中 x 是骰子的结果。
我们可以使用这个概率密度函数来模拟一次掷骰子的结果。例如,如果我们想知道掷骰子得到3的概率,我们可以计算 f(3) = 1 / 6,得到的结果是 1/6,即约为 0.1667。
此外,我们还可以使用这个均匀分布来生成随机数。通过从均匀分布中随机抽样,我们可以模拟多次掷骰子的结果。每次抽样的结果将具有相等的概率,并且可以在[1, 2, 3, 4, 5, 6]中任意一个数值。
python实现
import random
def roll_dice():
return random.randint(1, 6)
# 掷骰子十次并输出结果
for _ in range(10):
result = roll_dice()
print("骰子结果:", result)
# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)
# PDF
plt.plot(np.linspace(-4, 4, 100),
stats.uniform.pdf(np.linspace(-4, 4, 100))
)
plt.fill_between(np.linspace(-4, 4, 100),
stats.uniform.pdf(np.linspace(-4, 4, 100)),
alpha=.15)
# CDF
plt.plot(np.linspace(-4, 4, 100),
stats.uniform.cdf(np.linspace(-4, 4, 100)),
)
# LEGEND
plt.text(x=-1.5, y=.7, s="pdf (normed)", rotation=65, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=-.4, y=.5, s="cdf", rotation=55, alpha=.75, weight="bold", color="#fc4f30")
# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE
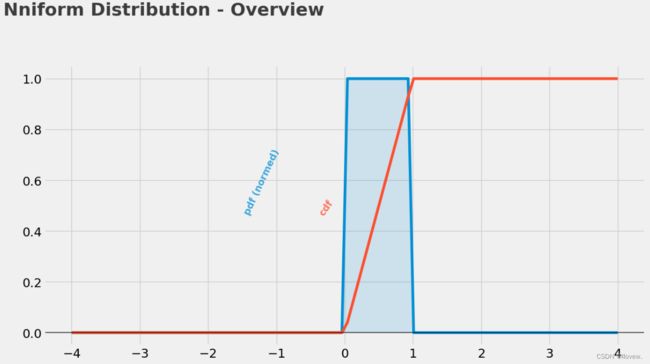
plt.text(x = -5, y = 1.25, s = "Nniform Distribution - Overview",
fontsize = 26, weight = 'bold', alpha = .75)卡方分布
通俗的说就是通过小数量的样本容量去预估总体容量的分布情况。
卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度。在计算卡方分布时,可以使用卡方检验来确定实际观测值与理论预期值之间的差异是否显著。卡方检验是一种常用的假设检验方法,可用于判断某个变量是否与其他变量相关。
公式
卡方分布建模实例
下面是一个使用卡方分布进行拟合度检验的实例,以说明如何进行建模:
假设我们有一组观测数据如下:
实际观测值:[10, 15, 20, 12, 8]
我们要检验这个观测数据是否符合一个假设的理论分布,比如均匀分布或正态分布。
首先,我们需要建立一个理论上的预期分布。在这个例子中,我们使用均匀分布作为理论分布。
接下来,我们计算理论预期值,可以假设每个观测值的预期值是一样的,即在均匀分布中每个值的概率是相等的。
对于均匀分布,我们可以假设每个值的预期概率为1/5,因为有5个不同的值。
理论预期值:[10, 10, 10, 10, 10]
接着,我们计算实际观测值与理论预期值之间的卡方值。计算公式如下:
卡方值 = ∑((观测值 - 预期值)^2 / 预期值)
在这个例子中,计算得到的卡方值为:
卡方值 = ((10-10)^2/10) + ((15-10)^2/10) + ((20-10)^2/10) + ((12-10)^2/10) + ((8-10)^2/10) = 4.4
最后,我们需要确定卡方值的显著性水平。根据卡方分布的自由度,我们可以查找对应的临界值,来判断卡方值的显著性。
计算得到的卡方值可以与临界值进行比较。如果卡方值超过了临界值,我们可以拒绝假设的理论分布,说明实际观测值与理论预期值不符合。如果卡方值未超过临界值,则无法拒绝假设的理论分布,说明实际观测值与理论预期值是一致的。
这是一个简单示例,展示了如何使用卡方分布进行拟合度检验的建模过程。实际应用中还会根据具体问题进行更复杂的分析和判断。
# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)
# PDF
plt.plot(np.linspace(0, 20, 100),
stats.chi2.pdf(np.linspace(0, 20, 100), df=4) ,
)
plt.fill_between(np.linspace(0, 20, 100),
stats.chi2.pdf(np.linspace(0, 20, 100), df=4) ,
alpha=.15,
)
# CDF
plt.plot(np.linspace(0, 20, 100),
stats.chi2.cdf(np.linspace(0, 20, 100), df=4),
)
# LEGEND
plt.xticks(np.arange(0, 21, 2))
plt.text(x=11, y=.25, s="pdf (normed)", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=11, y=.85, s="cdf", alpha=.75, weight="bold", color="#fc4f30")
# TICKS
plt.xticks(np.arange(0, 21, 2))
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE, SUBTITLE & FOOTER
plt.text(x = -2, y = 1.25, s = r"Chi-Squared $(\chi^{2})$ Distribution - Overview",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -2, y = 1.1,
s = 'Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a Chi-Squared distributed random variable $ y \sim \chi^{2}(k) $, given $k$=4.',
fontsize = 19, alpha = .85)beta分布
beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
Beta分布的形状取决于参数α和β的值。当α和β的值较大时,Beta分布接近于一个对称的钟形曲线。当α和β的值分别小于1时,Beta分布是一个倾斜的分布,具有较多的质量集中在0或1附近。
Beta分布在统计学中经常用于表示随机变量的概率分布,尤其在贝叶斯统计中具有重要的应用。它可以用于建模和推断二元事件的概率,例如成功和失败的概率、点击率等。
公式
# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML
# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)
plt.figure(dpi=100)
# PDF
plt.plot(np.linspace(0, 1, 100),
stats.beta.pdf(np.linspace(0, 1, 100),a=2,b=2)
)
print (stats.beta.pdf(np.linspace(0, 1, 100),a=2,b=2))
plt.fill_between(np.linspace(0, 1, 100),
stats.beta.pdf(np.linspace(0, 1, 100),a=2,b=2),
alpha=.15
)
# CDF
plt.plot(np.linspace(0, 1, 100),
stats.beta.cdf(np.linspace(0, 1, 100),a=2,b=2),
)
# LEGEND
plt.text(x=0.1, y=.7, s="pdf (normed)", rotation=52, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=0.45, y=.5, s="cdf", rotation=40, alpha=.75, weight="bold", color="#fc4f30")
# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)
# TITLE, SUBTITLE & FOOTER
plt.text(x = -.125, y = 1.85, s = "Beta Distribution - Overview",
fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -.125, y = 1.6,
s = 'Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a beta distributed random variable ' + r'$ y \sim Beta(\alpha, \beta)$, given $ \alpha = 2 $ and $ \beta = 2$.',
fontsize = 19, alpha = .85)