数字信号处理翻转课堂笔记20——FIR滤波器各种结构（直接型、级联型、线性相位结构、频率采样结构）

数字信号处理翻转课堂笔记20

The Flipped Classroom20 of DSP

对应教材：《数字信号处理（第五版）》西安电子科技大学出版社，丁玉美、高西全著

一、要点

1、FIR数字滤波器的直接型和级联型实现网络结构；
2、FIR数字滤波器的线性相位网络结构（重点）；
3、FIR数字滤波器的频率采样网络结构（难点）；
4、格型网络结构。

二、问题与解答

1、自定FIR线性相位数字滤波器类型和技术指标，基于MATLAB设计一个阶次在40~100之间的FIR滤波器。分别采样直接型和级联型结构实现，通过微调部分滤波器系数（参照第15次课关于IIR滤波器实现结构第3、4题的方式），分析不同网络结构条件下，系数的细微变化对滤波器特性的影响（通过系数变化前后零点图的变化和滤波器幅频特性的变化来分析）。
2、与直接型结构相比，FIR滤波器的线性相位结构有何优势？不同类型线性相位、不同长度FIR滤波器的线性相位结构主要有什么区别？任意给定一个长度为12~20的FIR线性相位滤波器，画出其线性相位结构。
3、线性相位结构是否也可以采用级联的方式来实现？为什么？试举例进行说明。
4、为什么频率采样结构不适用于IIR滤波器？简述频率采样结构的原理和组成，为什么它特别适合于窄带滤波器？自定一个FIR窄带滤波器并取适当的滤波器长度，用频率采样法设计出该滤波器，分析若分别用直接型结构和频率采样结构来实现（不必画出具体的实现结构图），哪一种结构更为简单？
5、频率采样结构在实际应用中为什么要进行修正？对于上一题设计的滤波器，分别用无修正（r=1）和有修正（r<1）的频率采样结构来实现。基于MATLAB，自行设定一个滤波器输入信号（至少分别含有滤波器通带和阻带的频率分量），用这两种实现结构对该信号进行滤波，比较滤波结果的差异（分别比较输出信号的波形和频谱），若短时间内差异不明显，可尝试稍延长输入信号的长度。亦可进一步分析不同的r对滤波结果的影响。注意此时没有现成的函数来进行信号的滤波，需要根据频率采样结构的实现原理，逐点计算滤波输出。滤波输出到达稳态之前会有一个过渡过程，主要观测分析稳态的输出。

1、直接型和级联型结构实现数字滤波器

自定FIR线性相位数字滤波器类型和技术指标，基于MATLAB设计一个阶次在40~100之间的FIR滤波器。分别采样直接型和级联型结构实现，通过微调部分滤波器系数（参照第15次课关于IIR滤波器实现结构第3、4题的方式），分析不同网络结构条件下，系数的细微变化对滤波器特性的影响（通过系数变化前后零点图的变化和滤波器幅频特性的变化来分析）。

---

%%      代码：
clear all
Bt=pi/12;
wp=pi/6;
m=1;
N=ceil((m+1)*2*pi/Bt);
N=N+mod(N+1,2);             %使N为奇数
fprintf('N=%4d\n',N);      %显示滤波器阶数
Np=fix (wp/(2*pi/N))
Ns=N-2*Np-1;
w=2*pi*[0:N-1]/N;
Hk=[ones(1,Np+1),zeros(1,Ns),ones(1,Np)];
T=0.38;
Hk(Np+2)=T;Hk (N-Np)=T;     %加一个过渡采样
thetak=-pi*(N-1)*(0:N-1)/N; %相位采样向量
Hdk=Hk.*exp (j*thetak);
hn=real(ifft (Hdk));
Hw=fft(hn,1024);
wk=2*pi*[0:1023]/1024;
Hgw=Hw.*exp(j*wk*(N-1)/2);

figure(1);
plot (wk/pi,abs (Hgw));
grid on;
xlabel('频率（w/pi)');
ylabel('幅度（dB)');
title('滤波器的频率特性');
axis([0,1,-inf,inf]);

figure(2)
zplane(hn,1)
title('滤波器的极点分布');
axis([-2,2,-2,2]);
[sos,g]=tf2sos(hn,1);
hn(25)=0.9*hn(25);

figure(3);
wki=2*pi*(0:511)/512;
Hki=fft(hn,512);
plot(wki/pi,abs (Hki));
grid on;
xlabel('频率（w/pi)');
ylabel('幅度（dB)');
title('直接实现改变一个分子系数之后的幅频特性');
axis([0,1,-inf,inf]);
grid off;
sos(:,2)=0.99*sos(:,2);
[B1,A1]=sos2tf(sos,g);

figure(4);
zplane(hn,1);
title('直接实现改变一个分子系数之后的极点分布');

figure(5)
Hki=freqz(B1,A1,512);
plot(wki/pi,abs (Hki));grid on
xlabel('频率（w/pi)');
ylabel('幅度（dB)');
title('级联实现改变各级分子系数之后的幅频特性');
axis([0,1,-inf,inf]);
N=49;

figure(6)
zplane(B1,A1)
title('级联实现改变各级分子系数之后的极点分布');
axis([-2,2,-2,2]);

未改变时：


直接改变一个分子系数之后：

级联改变一个分子之后：


由以上结果可知：
级联型结构的特点：
①调整零点位置方便。
②运算量相比直接型大，
优点：
①硬件实现时，可以用一个二阶节进行时分复用
②每一个基本节系数变化只影响该子系统的零极点
③对系数变化的敏感度小，受有限长的影响比直接型低

2、FIR滤波器线性相位结构

与直接型结构相比，FIR滤波器的线性相位结构有何优势？不同类型线性相位、不同长度FIR滤波器的线性相位结构主要有什么区别？任意给定一个长度为12~20的FIR线性相位滤波器，画出其线性相位结构。

---

优势：网络具有线性相位特性，比直接型结构节约了近一半的乘法器。

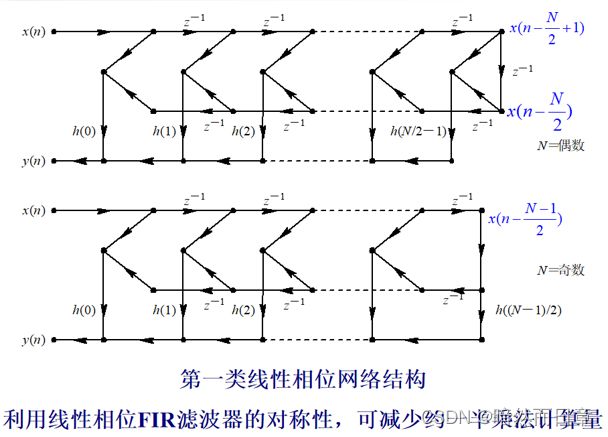
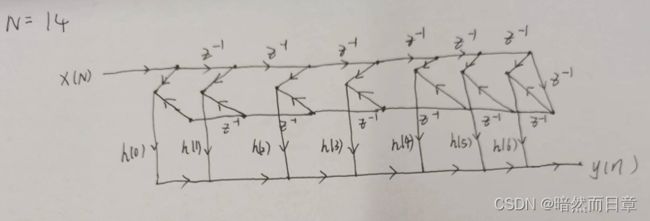
3、线性相位结构的实现方式

线性相位结构是否也可以采用级联的方式来实现？为什么？试举例进行说明。

---

（级联后的每级应该是偶对称，有些级联后的各级有不是偶对称的情况，因此线性相位结构不能采用级联方式实现）
①直接型可以采用级联的方式来实现，只是当H(z)阶数较高时不易因式分解故阶数高时不易实现
②

4、频率采样结构

为什么频率采样结构不适用于IIR滤波器？简述频率采样结构的原理和组成，为什么它特别适合于窄带滤波器？自定一个FIR窄带滤波器并取适当的滤波器长度，用频率采样法设计出该滤波器，分析若分别用直接型结构和频率采样结构来实现（不必画出具体的实现结构图），哪一种结构更为简单？

---

（1）频域率等间隔采样，相应的时域信号会以采样点数为周期进行周期性延拓，如果在频率域采样点数N大于等于原序列的长度M，则不会引起信号失真。IIR滤波器是无限长单位脉冲响应滤波器，采用频域采样的方法存在时域混叠的问题，所以频率采样结构不适用于IIR滤波器。
（2）频率采样结构的原理和组成：

当采样点数N很大时,，需要的乘法器和延时单元很多。但窄带滤波器大部分频率采样值H(k)为零，网络个数大大减少。所以频率采样结构适用于窄带滤波器。

5、频率采样结构的修正

频率采样结构在实际应用中为什么要进行修正？对于上一题设计的滤波器，分别用无修正（r=1）和有修正（r<1）的频率采样结构来实现。基于MATLAB，自行设定一个滤波器输入信号（至少分别含有滤波器通带和阻带的频率分量），用这两种实现结构对该信号进行滤波，比较滤波结果的差异（分别比较输出信号的波形和频谱），若短时间内差异不明显，可尝试稍延长输入信号的长度。亦可进一步分析不同的r对滤波结果的影响。注意此时没有现成的函数来进行信号的滤波，需要根据频率采样结构的实现原理，逐点计算滤波输出。滤波输出到达稳态之前会有一个过渡过程，主要观测分析稳态的输出。

---

需要修正的原因为：

x=cos(0.5pin)+cos(0.2pin);
采用窄带（带通滤波器），将0.2pi的频率分量滤除，只剩0.5pi频率分量；

clear;
N=69;
k=0:N-1;
th=exp(j*(-N+1)/N*pi*k);
Hg=[0 zeros(1,15) ones(1,4)  zeros(1,15) zeros(1,15)  ones(1,4) zeros(1,15)];
H=Hg.*th;
h=real(ifft(H))
h(69:-1:36)=h(1:34);
A=[1 zeros(1,68)];

figure(1)
freqz(h,A);

figure(2)
[H1,w]=freqz(h,A);
plot(w/pi,abs(H1));
L=10000;
n=0:L;
r=0.99;
x=cos(0.5*pi*n)+cos(0.2*pi*n);
for m=1:L+1
    if m>69
        x1(m)=x(m)-r^N*x(m-69);
    else
        x1(m)=x(m)-r^N*(cos(0.5*pi*(m-70))+cos(0.2*pi*(m-70)));
        %x1(m)=x(m);
    end
end;
yy=zeros(1,L+1);
for k=16:19
    y(2)=0;
    y(1)=0;
    for m=3:L+1
        y(m)=2*r*cos(2*pi/N*k)*y(m-1)-r^2*y(m-2)+2*real(H(k+1))*x1(m)-2*real(r*H(k+1)*exp(-j*2*pi/N*k))*x1(m-1);
    end;
    yy=yy+y;
end;
yy=yy/N;

figure(3)
stem(n(2200:2400),yy(2200:2400))
title('频率采样结构滤波输出')

figure(4)
Y=abs(fftshift(fft(yy(2000:10000))));
plot(0:0.00025:1,Y(4000:8000));

figure(5)
stem(cos(0.5*pi*(0:99)))
title('理想滤波输出')

由图可以观察到：
无修正时，有其他的频率分量(0.2pi)且输出不稳定。
不进行修正时，进行滤波系统会不稳定，而进行滤波时，与单位圆相差太多滤波效果太差不能满足要求，R越接近于1，滤波效果越好，甚至可以在保证滤波器稳定的条件下与理想滤波的差异忽略不计。

三、反思总结

暂无