D15+D16|递归好难！！！

222.完全二叉树的节点个数

其处理方法分为：1）按普通树来处理

                             2）按完全二叉树来处理

1）按完全二叉树来处理，我们可以按照其特性，寻找其中的满二叉树，然后满二叉树的计算规则2^n-1,再加上根节点的。

2）如何判断是否为满二叉树：

        判断其向左递归的深度和向右递归的深度是否相等。

class Solution {
    /**
     * 针对完全二叉树的解法
     *
     * 满二叉树的结点数为：2^depth - 1
     */
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        TreeNode left = root.left;
        TreeNode right = root.right;
        int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
        while (left != null) {  // 求左子树深度
            left = left.left;
            leftDepth++;
        }
        while (right != null) { // 求右子树深度
            right = right.right;
            rightDepth++;
        }
        if (leftDepth == rightDepth) {
            return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
        }
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

1)使用位运算计算2的n次方，从而depth是从0开始的

2）递归三部曲：

        a.输入输出：输入根节点，返回根节点下所有节点的数目 

        b.终止条件：判断其子树是不是满二叉树，如果是则利用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的：

        c.单层逻辑：

int leftTreeNum = countNodes(root->left);       // 左
int rightTreeNum = countNodes(root->right);     // 右
int result = leftTreeNum + rightTreeNum + 1;    // 中
return result;

---

110.平衡二叉树

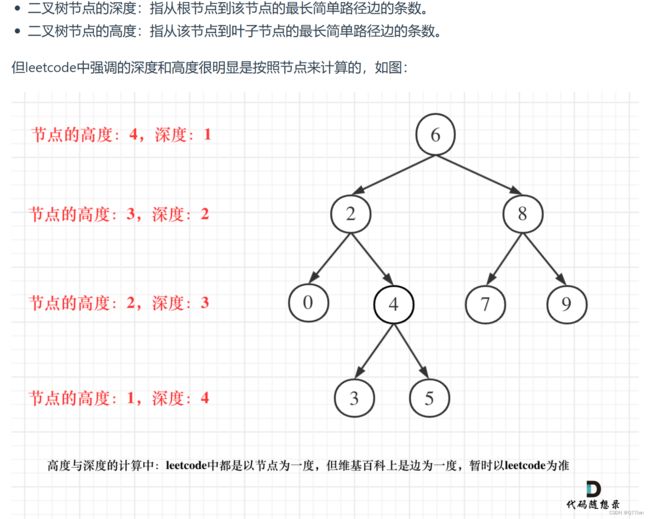
高度和深度

初始思路：

        很混乱。

题解复盘：

        递归三部曲：

        1）输入输出：输入一个节点（TreeNode），输出（int）（如果两边平衡的话输出高度，如果两边不平衡的话，返回-1）

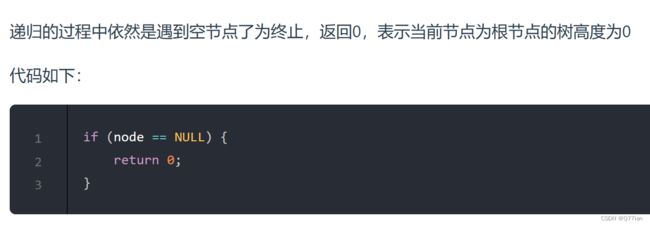
        2）终止条件：因为是计算高度，如果是空节点就返回高度是0

                                

        3）单层循环逻辑：

        计算左侧高度，计算右侧高度，最终高度为左右高度中的最大值+1

---

257. 二叉树的所有路径

题解复盘：

        递归加回溯是吧，那我就先看题解了。

           递归三部曲：

        1）输入输出：输入：根节点，记录本次路径的path，记录所有路径的result。

                                输出：void无需返回值

        2）终止条件：如果当前节点是叶子节点，就将本次路径转换为String然后添加进result。

        3）单层循环逻辑：前序

        首先将当前节点加入path

        如果左侧节点不为0就继续寻找路径，进行一次回溯

        如果右侧节点不为0就继续寻找路径，进行一次回溯

class Solution {
    /**
     * 递归法
     */
    public List binaryTreePaths(TreeNode root) {
        List res = new ArrayList<>();// 存最终的结果
        if (root == null) {
            return res;
        }
        List paths = new ArrayList<>();// 作为结果中的路径
        traversal(root, paths, res);
        return res;
    }

    private void traversal(TreeNode root, List paths, List res) {
        paths.add(root.val);// 前序遍历，中
        // 遇到叶子结点
        if (root.left == null && root.right == null) {
            // 输出
            StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串，速度更快
            for (int i = 0; i < paths.size() - 1; i++) {
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size() - 1));// 记录最后一个节点
            res.add(sb.toString());// 收集一个路径
            return;
        }
        // 递归和回溯是同时进行，所以要放在同一个花括号里
        if (root.left != null) { // 左
            traversal(root.left, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
        if (root.right != null) { // 右
            traversal(root.right, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
    }
}

        回溯，回溯了什么？

        就比如

        我第一次进入去寻找root.left的路径，我path里面其实变成12了，但是我去findright的时候我里面一开始只有1，所以在findleft之后，要删一下left，这就是回溯了一下。

       

---

404.左叶子之和

        节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

// 层序遍历迭代法
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        int sum = 0;
        if (root == null) return 0;
        Queue queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode node = queue.poll();
                if (node.left != null) { // 左节点不为空
                    queue.offer(node.left);
                    if (node.left.left == null && node.left.right == null){ // 左叶子节点
                        sum += node.left.val;
                    }
                }
                if (node.right != null) queue.offer(node.right);
            }
        }
        return sum;
    }
}

---

513.找树左下角的值

初始思路：

        层序遍历,只需要记录最后一行第一个节点的数值就可以了。

class Solution {
    public int findBottomLeftValue(TreeNode root) {        Queue que = new LinkedList<>();
        if(root!=null){que.offer(root);}
        List> result = new ArrayList<>();
        while(que.size()!=0){
            int size = que.size();
            List res = new ArrayList<>();
            while(size>0){
                TreeNode node = que.poll();
                res.add(node.val);
                if(node.left!=null){que.offer(node.left);}
                if(node.right!=null){
                    que.offer(node.right);
                }
                size--;
            }
            result.add(res);
        }

    return result.get(result.size()-1).get(0);
        

    }
}

 题解复盘：

保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。

        递归相较于层序遍历更难一点。

        1）输入输出：

参数必须有要遍历的树的根节点，还有就是一个int型的变量用来记录最长深度。 这里就不需要返回值了，所以递归函数的返回类型为void。

本题还需要类里的两个全局变量，maxLen用来记录最大深度，result记录最大深度最左节点的数值。

代码如下：

int maxDepth = INT_MIN;   // 全局变量 记录最大深度
int result;       // 全局变量 最大深度最左节点的数值
void traversal(TreeNode* root, int depth)

        注意此处为全局变量       

2）终止条件：

当遇到叶子节点的时候，就需要统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度。

代码如下：

if (root->left == NULL && root->right == NULL) {
    if (depth > maxDepth) {
        maxDepth = depth;           // 更新最大深度
        result = root->val;   // 最大深度最左面的数值
    }
    return;
}

                两个更新并且return   

    3）单层循环逻辑：

                    // 中
if (root->left) {   // 左
    depth++; // 深度加一
    traversal(root->left, depth);
    depth--; // 回溯，深度减一
}
if (root->right) { // 右
    depth++; // 深度加一
    traversal(root->right, depth);
    depth--; // 回溯，深度减一
}
return;

---

112. 路径总和 

初始思路：

        在找二叉树的所有路径中我们已经可以得到所有路径了，那么得到所有路径的和也不是一件难事，最后再在结果中find是否有target就可以了。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        List path = new ArrayList<>();
        List result = new ArrayList<>();
        if(root==null){return false;}
        pathSum(root,path,result);
        for(int i:result){
            if(i==targetSum){return true;}

        }
        return false;

    }
    public void pathSum(TreeNode root,List path,List result){
        if(root!=null){path.add(root.val);}
        
        if(root.left==null&&root.right==null){
            int sum = 0;
            for(int i :path){
                sum = sum+i;
            }
            result.add(sum);

        }
        if(root.left!=null){
            pathSum(root.left,path,result);
            path.remove(path.size()-1);

        }
        if(root.right!=null){
            pathSum(root.right,path,result);
            path.remove(path.size()-1);
            
        }
    }
}

题解复盘：

class solution {
   public boolean haspathsum(treenode root, int targetsum) {
        if (root == null) {
            return false;
        }
        targetsum -= root.val;
        // 叶子结点
        if (root.left == null && root.right == null) {
            return targetsum == 0;
        }
        if (root.left != null) {
            boolean left = haspathsum(root.left, targetsum);
            if (left) {      // 已经找到
                return true;
            }
        }
        if (root.right != null) {
            boolean right = haspathsum(root.right, targetsum);
            if (right) {     // 已经找到
                return true;
            }
        }
        return false;
    }
}

1. 确定递归函数的参数和返回类型

        参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

        如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）（有就行不用遍历全部？）遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

    2.确定终止条件（用递减，谁一开始能想到啊！）

        首先计数器如何统计这一条路径的和呢？

        不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

        如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

        如果遍历到了叶子节点，count不为0，就是没找到。

        3.确定单层循环条件

        前序，如果当前节点为叶子节点且count=0，就return true

        不然再继续其左，其右。

---

106.从中序与后序遍历序列构造二叉树

题解复盘：

来看一下一共分几步：

• 第一步：如果数组大小为零的话，说明是空节点了。

• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

• 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

• 第五步：切割后序数组，切成后序左数组和后序右数组

• 第六步：递归处理左区间和右区间

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
               if(postorder.length == 0 || inorder.length == 0)
            return null;
        TreeNode root = Treebuild(inorder,0,inorder.length,postorder,0,postorder.length);
        return root;

    }
    public TreeNode Treebuild(int[] inorder,int inorderbegin,int inorderend,int[] postorder,int postorderbegin, int postorderend){
        if(postorderbegin == postorderend)
            return null;
        TreeNode node = new TreeNode(postorder[postorderend-1]);
        if(postorderend==0){return node;}
        int rootindex = 0;;
        for(int i = inorderbegin;i

前序：

   root.left = Treebuild(preorder,preorderbegin+1,preorderbegin+(rootindex-inorderbegin)+1,inorder,inorderbegin,rootindex);
   root.right = Treebuild(preorder,preorderbegin+(rootindex-inorderbegin)+1,preorderend,inorder,rootindex+1,inorderend);

注意因为是左闭右开区间：

所以后序时postorderbegin+(rootindex - inorderbegin))

前序时preorderbegin+(rootindex-inorderbegin)+1

主要原因在于每次preorderbegin都要+1，很重要！！！我的报错原因