MIA-Net:用于多模态情感分析的多模态交互注意力网络
MIA-Net:用于多模态情感分析的多模态交互注意力网络
总括:多模态融合时,首先将多种模态分为主模态与辅助模态,通过构建了一个交互注意力模块,从辅助模态中提取对主模态有帮助的信息进行融合。
(属于特征级基于注意力的融合方式)
文章信息
作者:Shuzhen Li, Tong Zhang
单位:South China University of Technology(华南理工大学)
期刊:IEEE Transactions on Affective Computing
题目:MIA-Net: Multi-Modal Interactive Attention Network for Multi-Modal Affective Analysis
年份:2023
研究目的
探究如何在有限的计算量以及参数条件下,将双模态模型推广到三模态或多模态任务?以及不同模态对情感分析的不同贡献如何解决?
研究内容
提出了一种支持三模态或者多模态的融合模型MIA-Net(多模态交互式注意力网络),用于将主要模态和辅助模态进行融合,并用于情感分析。
研究方法
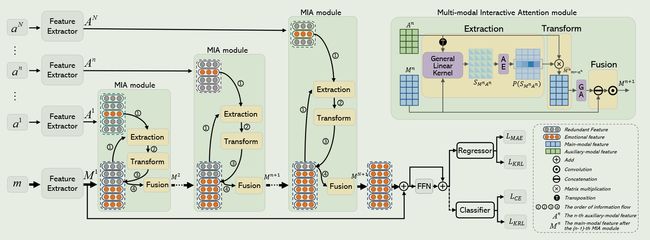
这个框架是由单模态特征提取器(Feature Extractor)、N-1个 MIA module、回归器与分类器构成的。
Feature Extractor
对于文本数据:首先利用了一个GPT-2(是一个标记符号化器),将每个文本描述标记为一系列的符号。然后利用RoEBRTa模型去提取文本特征。
对于音频数据:首先利用VQ-Wav2Vec模型,将音频的变长音频表征转换为离散音频表征,然后仍旧是利用RoBERTa模型,从离散的声学表征中提取声学特征。
对于视频数据:首先采用RetinaFace模型,将每个视频帧中的面部区域进行检测与分割。然后根据关键帧的数量,从每个视频中提取视频帧。最后利用Fabnet模型,从提取的视频帧中提取视觉特征。
文本特征维度:1024,声学特征维度:768,视觉特征维度:256
MIA module
符号表示:
M j n M_{j}^{n} Mjn表示 M n M^n Mn的第 j j j个主模态特征向量, A i n \mathbf{A}_i^n Ain表示 A n A^n An的第 i i i个辅助模态特征向量。
K ( A i n , M j n ) \mathcal{K}(\boldsymbol{A}_i^n,\boldsymbol{M}_j^n) K(Ain,Mjn)代表一般General Linear Kernel,用于计算 S M n A n S_{\boldsymbol{M}^n\boldsymbol{A}^n} SMnAn(代表亲和矩阵)。
P ( S M n A n ) \boldsymbol{P}(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n}) P(SMnAn)表示交互注意力权重,用于改进主模态表征。
P j i ( S M n A n ) \boldsymbol{P}_{ji}(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n}) Pji(SMnAn)表示第 i 个辅助模态特征向量对第 j 个主模态特征向量的重要性。
M ^ m ← a n n \hat{\boldsymbol{M}}_{m\gets a^n}^n M^m←ann表示由辅助模态增强的更新后的主模态特征。
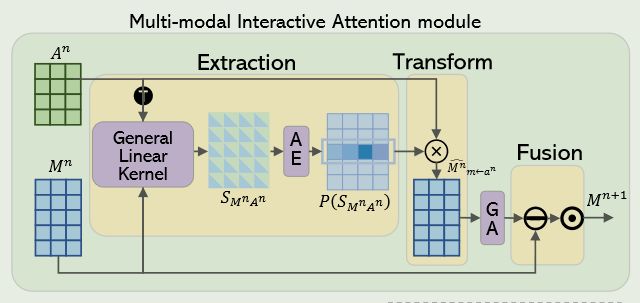
每个MIA module是由提取、转换、融合这三个子模块构成的。MIA module的作用就是从辅助模态中选择重要的特征去改进主模态特征。
Extraction
首先利用一般线性内核去捕捉模态特征之间的相似性,然后就得到了一个亲和矩阵 S M n A n S_{\boldsymbol{M}^n\boldsymbol{A}^n} SMnAn。
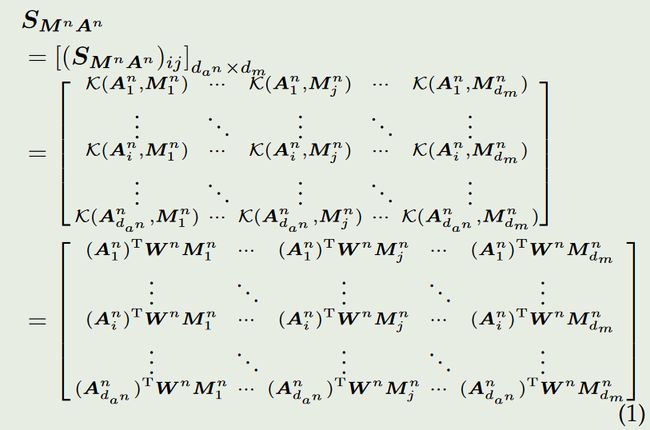
k ( x , y ) = x T W y \begin{aligned}k(x,y)=x^{T}Wy\end{aligned} k(x,y)=xTWy
要满足此式,W必须是一个半正定矩阵,半正定矩阵实际上就是一个实对称矩阵。
每个实对称矩阵又可以被分解为正交矩阵。(根据定理 Q = P T Λ P Q=\boldsymbol{P^\mathrm{T}}\boldsymbol{\Lambda P} Q=PTΛP)所以一般线性内核最终的计算公式为:
K ( A i n , M j n ) = ( A i n ) T W n M j n = ( A i n ) T ( P n ) T Λ P n M j n = ( P n A i n ) T Λ ( P n M j n ) . \begin{aligned} \mathcal{K}(\boldsymbol{A}_i^n,\boldsymbol{M}_j^n)& =\left(\boldsymbol{A}_i^n\right)^\mathrm{T}\boldsymbol{W}^n\boldsymbol{M}_j^n \\ &=\left(\boldsymbol{A}_i^n\right)^{\mathrm{T}}(\boldsymbol{P}^n)^{\mathrm{T}}\boldsymbol{\Lambda}\boldsymbol{P}^n\boldsymbol{M}_j^n \\ &=\left(\boldsymbol{P}^n\boldsymbol{A}_i^n\right)^\mathrm{T}\boldsymbol{\Lambda}(\boldsymbol{P}^n\boldsymbol{M}_j^n). \end{aligned} K(Ain,Mjn)=(Ain)TWnMjn=(Ain)T(Pn)TΛPnMjn=(PnAin)TΛ(PnMjn).
在得到亲和矩阵(两种模态之间的相似性)之后,通过编码器AE,将亲和矩阵编码为交互注意力权重 P ( S M n A n ) \boldsymbol{P}(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n}) P(SMnAn),通过 P ( S M n A n ) \boldsymbol{P}(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n}) P(SMnAn),去改进主模态的特征。
P ( S M n A n ) = [ P 1 ( S M n A n ) , ⋯ , P j ( S M n A n ) , ⋯ , P d m ( S M n A n ) ] P(S_{\boldsymbol{M}^n\boldsymbol{A}^n})=\left[P_1(S_{\boldsymbol{M}^n\boldsymbol{A}^n}),\cdots,P_j(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n}),\cdots,P_{dm}(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n})\right] P(SMnAn)=[P1(SMnAn),⋯,Pj(SMnAn),⋯,Pdm(SMnAn)]
P j ( S M n A n ) = [ P j 1 ( S M n A n ) ⋮ P j i ( S M n A n ) ⋮ P j d u n ( S M n A n A n ) ] = [ e x p ( K ( A 1 n , M j n ) ) ∑ k d a n e x p ( K ( A k n , M j n ) ) ⋮ e x p ( K ( A i n , M j n ) ) ∑ k d a n e x p ( K ( A k n , M j n ) ) ⋮ e x p ( K ( A d a n n , M j n ) ) ∑ k d a n e x p ( K ( A i n , M j n ) ) ] P_j(S_{\boldsymbol{M}^n\boldsymbol{A}^n})=\begin{bmatrix}P_{j1}(S_{\boldsymbol{M}^n\boldsymbol{A}^n})\\\vdots\\P_{ji}(S_{\boldsymbol{M}^n\boldsymbol{A}^n})\\\vdots\\P_{jd_{u^n}}(S_{\boldsymbol{M}^n\boldsymbol{A}^n\boldsymbol{A}^n})\end{bmatrix}=\begin{bmatrix}\frac{exp(\mathcal{K}(\boldsymbol{A}_1^n,\boldsymbol{M}_j^n))}{\sum_k^{d_a\boldsymbol{n}}exp(\mathcal{K}(\boldsymbol{A}_k^n,\boldsymbol{M}_j^n))}\\\vdots\\\frac{exp(\mathcal{K}(\boldsymbol{A}_i^n,\boldsymbol{M}_j^n))}{\sum_k^{d_an}exp(\mathcal{K}(\boldsymbol{A}_k^n,\boldsymbol{M}_j^n))}\\\vdots\\\frac{exp(\mathcal{K}(\boldsymbol{A}_{d_a^n}^n,\boldsymbol{M}_j^n))}{\sum_k^{d_an}exp(\mathcal{K}(\boldsymbol{A}_i^n,\boldsymbol{M}_j^n))}\end{bmatrix} Pj(SMnAn)= Pj1(SMnAn)⋮Pji(SMnAn)⋮Pjdun(SMnAnAn) = ∑kdanexp(K(Akn,Mjn))exp(K(A1n,Mjn))⋮∑kdanexp(K(Akn,Mjn))exp(K(Ain,Mjn))⋮∑kdanexp(K(Ain,Mjn))exp(K(Adann,Mjn))
Transform
通过Extraction得到了主模态与辅助模态之间的交互注意力权重 P ( S M n A n ) \boldsymbol{P}(\boldsymbol{S}_{\boldsymbol{M}^n\boldsymbol{A}^n}) P(SMnAn),然后在Transform模块中,将交互注意力权重与辅助模态特征进行矩阵相乘,得到新的主模态特征 M ^ m ← a n n \hat{\boldsymbol{M}}_{m\gets a^n}^n M^m←ann
然后将这个新的主模态特征,通过自门机制GA进行改进(提取更多的判别特征,并抑制可能存在的噪声特征),得到改进后的主模态特征 M g a t e d n M_{gated}^n Mgatedn。
M g a t e d n = M ^ m ← a n n ⋅ G G = σ ( K 1 ⊙ M ^ m ← a n n + b 1 ) M_{gated}^n=\hat{M}_{m\leftarrow a^n}^n\cdot\boldsymbol{G}\\ \boldsymbol{G}=\sigma(\boldsymbol{K}_1\odot\hat{\boldsymbol{M}}_{m\gets a^n}^n+\boldsymbol{b}_1) Mgatedn=M^m←ann⋅GG=σ(K1⊙M^m←ann+b1)
⊙ \odot ⊙表示卷积, σ \sigma σ代表logistic sigmoid激活函数,G代表门控系数。 K 1 K_1 K1和 b 1 b_1 b1分别代表卷积核与偏置。
Fusion
最后将门改进的主模态特征 M g a t e d n M_{gated}^n Mgatedn,与最初的主模态特征 M n M^n Mn进行融合。得到最终的融合后的模态特征。
M n + 1 = f N ( σ ( K 2 ⊙ [ M g a t e d n : M n ] + b 2 ) ) \boldsymbol{M}^{n+1}=f_N(\sigma(\boldsymbol{K}_2\odot[\boldsymbol{M}_{gated}^n:\boldsymbol{M}^n]+\boldsymbol{b}_2)) Mn+1=fN(σ(K2⊙[Mgatedn:Mn]+b2))
f N ( ⋅ ) f_{N}(\cdot) fN(⋅)表示批量归一化函数, [ : ] \left[:\right] [:]表示连接操作
通过多个MIA module堆叠,最终得到通过N个辅助模态增强后的主模态特征。接着通过两个残差连接,得到了经过MIA-Net的最终主模态特征 M ˇ \check{\boldsymbol{M}} Mˇ.
残差连接
第一个残差连接:
M r e s = M 1 + M M I A s = M 1 + f M I A s ( M 1 , A 1 , ⋯ , A N ) \begin{aligned} \boldsymbol{M}_{res}& =\boldsymbol{M}^{1}+\boldsymbol{M}_{MIAs} \\ &=\boldsymbol{M}^1+\boldsymbol{f}_{MIAs}(\boldsymbol{M}^1,\boldsymbol{A}^1,\cdots,\boldsymbol{A}^N) \end{aligned} Mres=M1+MMIAs=M1+fMIAs(M1,A1,⋯,AN)
M M I A S M_{MIAS} MMIAS表示经过多个MIA module改进后的 M 1 M^1 M1的主模态特征。
M r e s M_{res} Mres表示残差主模态特征。
第二个残差连接:
M ˇ = M r e s + f F F N ( M r e s ) \check{M}=M_{res}+f_{FFN}(\boldsymbol{M}_{res}) Mˇ=Mres+fFFN(Mres)
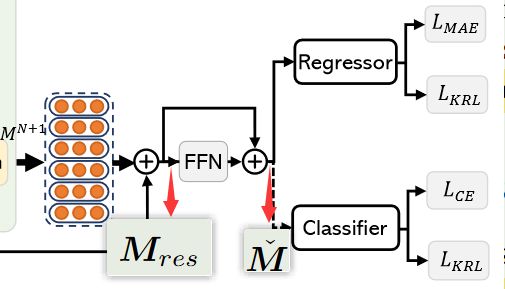
经过残差连接后的主模态特征 M ˇ \check{M} Mˇ送入Regressor或者Classifier进行最终的情感识别或情感分类。
Regression
回归模型由一个全连接层和一个联合损失构成。
联合损失如下:
L = ( 1 − γ ) L M A E + γ L K R L L M A E = − 1 N ∑ n = 1 N ∣ y ( n ) − z ( n ) ∣ z = θ T M ˇ + b 3 \mathcal{L}=(1-\gamma)\mathcal{L}_{MAE}+\gamma\mathcal{L}_{KRL}\\ \begin{gathered}\mathcal{L}_{MAE}=-\frac1N\sum_{n=1}^N|y^{(n)}-z^{(n)}|\\z=\boldsymbol{\theta}^\mathrm{T}\check{M}+\boldsymbol{b}_3\end{gathered} L=(1−γ)LMAE+γLKRLLMAE=−N1n=1∑N∣y(n)−z(n)∣z=θTMˇ+b3
L M A E \mathcal{L}_{MAE} LMAE代表平均绝对误差损失。 L K R L \mathcal{L}_{KRL} LKRL代表内核正则化损失( L K R L \mathcal{L}_{KRL} LKRL的用途是求亲和矩阵 S M n A n S_{\boldsymbol{M}^n\boldsymbol{A}^n} SMnAn时,保证 W W W为半正定矩阵)
Classifition
分类模型由一个全连接层、一个Softmax函数和一个联合损失构成。
联合损失如下:
L = ( 1 − γ ) L C E + γ L K R L L C E = − 1 N ∑ n = 1 N y n l o g ( P ( y ^ n ) ) P ( y ^ ) = s o f t m a x ( θ T M ˇ + b 3 ) . \begin{gathered} \mathcal{L}=(1-\gamma)\mathcal{L}_{CE}+\gamma\mathcal{L}_{KRL} \\ \begin{aligned}\mathcal{L}_{CE}=-\frac{1}{N}\sum_{n=1}^Ny_nlog(P(\hat{y}_n))\end{aligned} \\ \begin{aligned}P(\hat{y})=softmax(\boldsymbol{\theta^\mathrm{T}}\check{\boldsymbol{M}}+\boldsymbol{b_3}).\end{aligned} \end{gathered} L=(1−γ)LCE+γLKRLLCE=−N1n=1∑Nynlog(P(y^n))P(y^)=softmax(θTMˇ+b3).
L C E \mathcal{L}_{CE} LCE代表标准交叉熵损失。
结论与讨论
- 将MIA-Net模型与SOTA的一些模型在CMU-MOSI与CMU-MOSEI数据集上进行对照实验,MIA-NET效果最好。
- MIA-Net 在处理三种或三种以上模态的数据时是有效的。(消融研究)
- MIA-Net可以推广到新的数据集、任务以及模态上。(通用性研究)
- 多模态交互注意力模块能够有效实现辅助融合。(对提出的模态验证)
- 对超参数的研究。
- 联合损失是有效的。(对损失函数的研究)
- 与不同的融合方法进行对比。(证明本研究的实用性)
代码和数据集
代码没有公开
数据集:CMU-MOSI(1.5G),CMU-MOSEI(25G),MELD(10G)
GPU配置:没有提