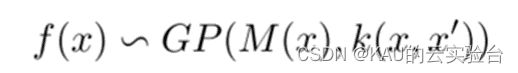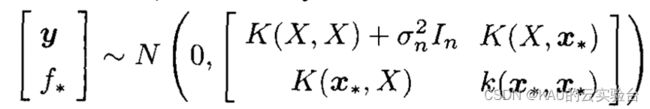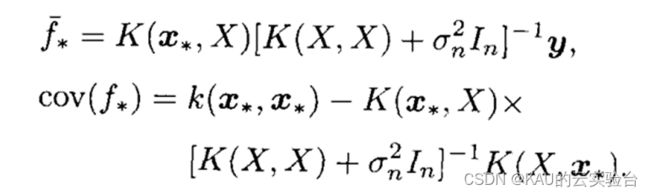预测算法|高斯过程回归GPR算法原理及其优化实现

目前，常用的机器学习方法主要有支持向量机（support vector machine，SVM)、反向传播神经网络（backpropagation neural network，BPNN)等非概率方法以及高斯过程回归(gaussian process regression，GPR)等概率方法。

而GPR作为一种非参数概率核模型[1]，不仅可以用于预测，而且可以为预测中的每个点提供置信度区间，从而将预测的不确定性量化，并且GPR有着严格的统计学习理论基础，对处理高维数、小样本、非线性等复杂的问题具有很好的适应性。且GPR泛化能力强，与神经网络、支持向量机相比，具有容易实现、超参数自适应获取、非参数推断灵活以及输出具有概率意义等优点。

本文将介绍GPR的原理及其优化实现（很久前一位粉丝想看的内容）。​

00 目录

1 GPR模型原理

2 优化算法及其改进概述

3 结合优化算法的GPR预测模型

4 实验结果

5 源码获取

01 GPR模型原理

GPR是一个植根于贝叶斯统计的较为流行的非参数机器学习技术，因为它能够在小数据集上有出色的预测准确性 [2]而没有过拟合或欠拟合的问题[3]，并且能够给出关于模型输出的不确定性的信息[4]。

GPR有三个主要步骤：

(1) 根据主观的先验知识选择合适的核函数并定义初始超参数;

(2) 使用概率分布生成先验模型并对其进行训练，即通过训练样本寻找最优超参数;

(3) 对测试样本进行预测，给出估计结果的均值和方差。

在其中，如何获得最优超参是值得研究的问题，常见如传统的基于梯度算法或现代智能优化算法的方法都可用于其中，而负对数边际似然（NLML）值通常被设置为目标函数。

下面具体讲解一下GPR的理论内容[5]：

1.1 预测

高斯过程定义为随机变量的集合，其中任意点都服从联合高斯分布。这些变量由均值u（x）和协方差函数(也即核函数)k（x，x’）确定，其中协方差函数表示为空间中任意两个随机输入变量对应的随机输出变量的中心矩，能够用于衡量训练集与测试集相似或相关的程度，是影响 GPR 模型预测性能的关键因素。他们被定义为：

高斯过程(GP)为可表现为如下：

由于高斯过程灵活且性质主要由核函数所决定，一般使用GPR进行建模时，可假设其均值函数μ（x）=0，并预先选择核函数的形式。

实际数据通常包含一定噪声，因此对于回归模型，把噪声ε加入到观察目标数据y中，可以得到GPR模型：

其中: x为输入向量，f为函数值，y为受噪声污染的观测值，进一步假设噪声：

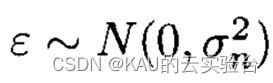
可以得到观测值y的先验分布为：

以及观测值y和预测值f*的联合先验分布为：

其中：K(X,X)为n阶对称正定的协方差矩阵，K(X，x*)=K(x*,X)T为测试点x*与训练集的输入X之间的协方差矩阵。

由此可以计算出预测值f*的后验分布为：

其中，

f-即为f的估计值，cov(f*)为测试样本的协方差矩阵。

1.2 训练

GPR的训练其实是选择合适的协方差函数以及确定其最优超参数的过程。不同的协方差函数确定了在该高斯过程先验下目标函数可能具有的性质。比如，周期协方差函数表示目标函数具有周期性；平方指数协方差函数表示目标函数具有无穷阶导数，即处处光滑。在实际应用中，使用最广泛的为平方指数协方差函数，具体形式如下：

式中，σ2f为信号方差，S＝dig(l^2)，l为输入向量各个维度的带宽，也叫方差尺度。每种不同的协方差函数都存在一些像σ2f和l这样的超参数，超参数的取值决定了协方差函数的具体形状，同时也决定了从高斯过程中所采样函数的特征。参数集合θ={S,σ2f,σ2n}即为超参数，一般通过采用共轭梯度下降法等优化方法使求偏导后的负对数边际似然(negative log marginal likelihood，NLML)最小化来求解超参数。NLML表示为：

获得最优超参数后，利用预测部分的最后一张图中的式子即可获得测试点预测值及其方差。

关于理论部分是作者根据自己的理解作出的简要阐述，因此可能有错误或讲的不清楚的地方，也推荐大家看以下的文献进行深入研究：

Nonparametric modeling of ship maneuvering motion based on Gaussian process regression optimized by genetic algorithm
MathWorks关于GPR的推导：https://ww2.mathworks.cn/help/stats/gaussian-process-regression-models.html
文献5

GPR可以优化的地方之一在于其优化方法上，其本身的共轭梯度寻优方法对初始值有很强的依赖性，但目前初始值的设定没有理论依据，若初始值设置不当，可能会使其在搜索过程中陷入局部最优甚至无法收敛，因此这部分可以引入优化算法进行提升。

02 优化算法及其改进概述

前面的文章中作者介绍了许多种优化算法及其改进算法，本文中作者以PSO、GWO、WOA、SSA为例进行展示。

03 结合优化算法的GPR预测模型

优化算法主要作用是寻找最优超参数，以GWO的优化过程为例，GWO-GPR的流程图如下：

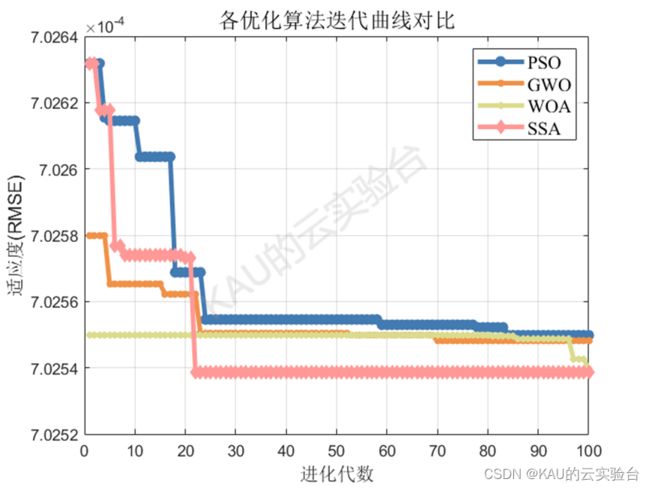
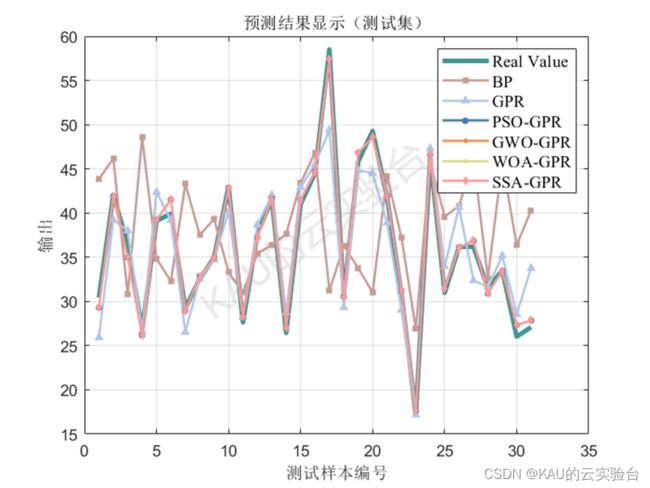
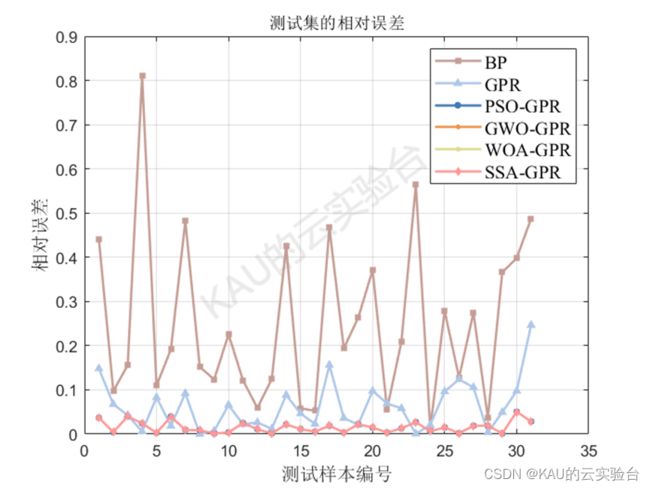
04 实验结果

以均方根差(Root Mean Square Error，RMSE) 、平均绝对百分误差( Mean Absolute Percentage Error，MAPE) 、平均绝对值误差 ( Mean Absolute Error，MAE) 和可决系数（coefficient of determination，R^2）作为评价标准。

05 源码获取

代码注释详细，一般只需要替换数据集就行了，注意数据的行是样本，列是变量，源码提供2个版本。

1.免费版

其主要是GPR预测模型，数据为多数入单输出，Matlab编写，对于需要进行一些简单预测或者是想学习GPR算法的MATLAB实现的同学足够了。

获取方式——公众号（KAU的云实验台）后台回复**：GPR**

不过通过MATLAB调用GPR模型时卡卡发现有些数据集会出现预测值有NaN的问题，目前这个问题我还不能解决，有知道的朋友也可以告诉一下我，改进成功的话卡卡可以请你喝杯奶茶嘿嘿。

2.付费版

包含BP、GPR、PSO-GPR、GWO-GPR、WOA-GPR、SSA-GPR预测模型程序（MATLAB），程序的注释详细，并且此程序进行优化算法的替换更为简单，卡卡之前介绍过的智能优化算法及其改进都可以进行替换。

由于前面说到的NaN值的问题，因此购买此版本之前建议先在免费版尝试一下各位的数据集是否可用，观察效果后再决定。

获取方式——公众号（KAU的云实验台）后台回复：IGPR 或 点击文末“ 阅读原文 ”

[1] Rasmussen，C.E.，2004. Gaussian processes in machine learning.

[2] A. Kamath, R.A. Vargas-Hern´andez, R.V. Krems, T. Carrington, S. Manzhos, Neural networks vs Gaussian process regression for representing potential energy surfaces:A comparative study of fit quality and vibrational spectrum accuracy, J. Chem.Phys. 148 (2018).

[3] C.F.G.D. Santos, J.P. Papa, Avoiding overfitting: A survey on regularization methods for convolutional neural networks, ACM Comput. Surv. (CSUR) 54 (2022)1–25.

[4] Wenqi, F., Shitia, Z., Hui, H., Shaobo, D., Zhejun, H., Wenfei, L., Zheng, W., Tianfu, S.,Huiyun, L., 2018. Learn to make decision with small data for autonomous driving:deep gaussian process and feedback control. J. Adv. Transp., 8495264.

[5]何志昆,刘光斌,赵曦晶等.高斯过程回归方法综述[J].控制与决策,2013,28(8):1121-1129,1137.

另：如果有伙伴有待解决的优化问题（各种领域都可），可以发我，我会选择性的更新利用优化算法解决这些问题的文章。

如果这篇文章对你有帮助或启发，可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行)。