c语言先序线索二叉树(超详细)学习笔记
前言:
本文章是继 上一篇我的文章 C语言中序线索二叉树(超详细)学习笔记 续写的先序顺序线索二叉树,若是不懂中序,想学先序,建议先看懂中序。
我的文章有点长,希望你能够耐心看完,一定一定会有所收获的!
一、创建二叉树结构体
因为线索二叉树 需要运用标记来区分是否有左孩子还有右孩子 所以定义 整型ltag和rtag,并规定 ltag= 0 代表有 左孩子,ltag = 1 代表没有左孩子;rtag = 0 代表有右孩子,rtag = 1 代表没有右孩子。
typedef struct TreeNode
{
int ltag, rtag;
char data;
struct TreeNode* lChild;
struct TreeNode* rChild;
}TreeNode;二、二叉树的初始化
1、初始化方式
仍是使用先序方式进行传入数据 并运用递归。如果想了解递归详细的推导,可以看看我的这篇文章 c语言二叉树的创建与前序、中序、后序遍历(超详细)学习笔记
TreeNode* creatTree()
{
TreeNode* T;
char ch;
scanf_s("%c", &ch);//通过输入的ch是否是‘#’来判断该节点是否有孩子节点
if (ch == '#')
{
//为空结点
return NULL;
}
else
{
T = (TreeNode*)malloc(sizeof(TreeNode));
T->data = ch;
T->ltag = 0;
T->rtag = 0;
printf("");
T->lChild = creatTree();
T->rChild = creatTree();
return T;
}
}2、注意
我在用vs2022 来编译时,发现初始化时 creatTree() 函数会 莫名其妙停下来,并不是代码出现了错误。经过我很多次测试,我认为原因是:二叉树结构体里定义太多变量时,就会莫名其妙停下,解决的方法就是再往此函数内 在做些什么 如是添加形参,添加输出语句 printf(""), 此函数才会正常往下运行。
三、先序线索遍历
思路:
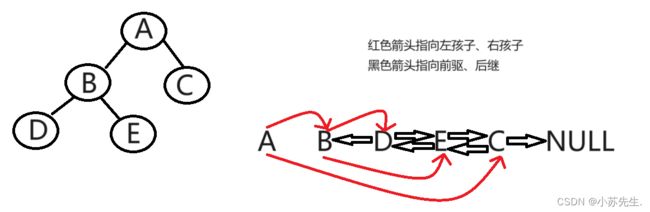
如图: 先序顺序为:根左右 A B D E C 有左孩子就指向左孩子,没有则指向前驱;有右孩子就指向右孩子,没有则指向后继;D没有左孩子也没有前驱,则指向NULL;C没有右孩子也没有后继则指向NULL;
代码:
void preThreadTree(TreeNode* T, TreeNode** pre)
{
if (T)//传进来的结点是否为空
{
if (T->lChild == NULL) //左孩子为空 指向前驱 假设当前为树结点 为 A
{
T->ltag = 1; //标记为1
T->lChild = *pre; //A的左孩子指向前驱元素 假设当前 前驱元素为B
}
if (*pre != NULL && (*pre)->rChild == NULL)//前驱元素B不为空 且 它的右孩子为空 指向后继元素 A
{
(*pre)->rtag = 1;//标记为1
(*pre)->rChild = T; //B的右孩子 指向 后继元素A
}
*pre = T;
if (T->ltag == 0)//如果有左孩子
{
preThreadTree(T->lChild, pre);//指向左孩子
}
preThreadTree(T->rChild, pre);//指向右孩子
}
}代码解释:
二级指针 是为了在函数体内可以改变指针的地址,即可以通过函数来改变实参的值,指针*pre的值可以随时改变。
先考虑框架 根左右 根:干事情 ;左: inThreadTree(T->lChild, pre);右: inThreadTree(T->rChild, pre) ; 再考虑核心 就是干事情。这一步代码里的注释很详细。假设当前树结点为A,前驱结点为B,前两个if语句都满足的情况下:
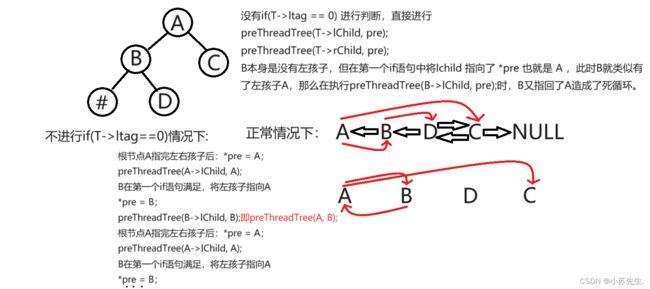
最后一个if语句判断当前结点是否有左孩子,没有再返回右孩子
这是必须考虑的,原因如下:
递归思路演示:
递归:分为递归分为两步,第一步到达函数最深层,第二步原路返回到函数第一层,并返回最终返回值。此递归函数为void类型递归,干事情在前,调用递归函数在后,只需要走第一步。详情:
可以看我的这篇文章:浅说递归的含义及递归的整个过程
前提:先将*pre = NULL(这步main函数将*pre初始化时就等于NULL);传入根节点A,T=A,第一个if语句A有左孩子,不满足,直接跳过;第二个if语句*pre == NULL,不满足,直接跳过;进行 *pre = T;将A 变为了 *pre(前驱元素)此时*pre不再为NULL ,第三个if语句 A有左孩子,进行 preThreadTree(T->lChild, pre);即(A的左孩子B,A);传入结点B,T = B,第一个if语句B有左孩子,不满足,直接跳过;第二个if语句A有右孩子不满足,直接跳过;进行 *pre = T;将B 变为了 *pre(前驱元素),第三个if语句B有左孩子,进行 preThreadTree(T->lChild, pre);即(B的左孩子D,B);传入结点D,T = D,第一个if语句D没有左孩子,满足条件,ltag = 1;并将指向左孩子改为指向前驱元素 T->lChild = *pre(解引用操作);所以A B <=D,第二个if语句B有右孩子不满足,直接跳过;进行 *pre = T;将D 变为了 *pre(前驱元素),第三个if语句D没有左孩子,进行preThreadTree(T->rChild, pre);即(D的右孩子,D);D的右孩子为空,即T = NULL,不会继续往下执行,即中断;完成了最深的左孩子D,该执行B的右孩子E了(继续往下递归直到最深层,遵循根左右原则,B的左孩子D干完了,就进行B的右孩子E了) 即 preThreadTree(B->rChild, D); 传入结点E,T = E,第一个if语句E没有左孩子,满足条件,并将指向左孩子改为指向前驱元素D,所以A B <=D<=E,第二个if语句D没有右孩子,满足条件,rtag = 1;并将指向右孩子该为指向E,所以A B <=D<= =>E,进行 *pre = T;将E 变为了 *pre(前驱元素),第三个if语句E没有左孩子,进行进行preThreadTree(T->rChild, pre);即(E的右孩子,E);E的右孩子为空,即T = NULL,不会继续往下执行,即中断;完成了左孩子B,该执行A的右孩子C了(继续往下递归到达最深层。遵循根左右原则,A的左孩子B干完了,就进行A的右孩子C了)即 preThreadTree(A->rChild, E); 传入结点C,第一个if语句C没有左孩子,满足条件,ltag = 1;并将指向左孩子改为指向前驱元素E,所以A B <=D<= =>E<=C,第二个if语句E没有右孩子,满足条件,rtag = 1;并将指向右孩子该为指向C,所以A B <=D<= =>E<= =>C,进行 *pre = T;将C 变为了 *pre(前驱元素),第三个if语句C没有左孩子,进行进行preThreadTree(T->rChild, pre);即(C的右孩子,C);C的右孩子为空,即T = NULL,不会继续往下执行,函数执行结束。最终效果为:A B <=D<= =>E<= =>C;所以我们在最后还得自己更改最后一个元素的右指向,使其rtag = 1,并将指向右孩子改为指向NULL。得到 A B <=D<= =>E<= =>C=>NULL
四、得到下一个元素函数
做第四步是为了最后用for循环将元素一个接着一个打印输出而准备。
代码注释的很详细,按照 有后继元素 输出 后继元素;没有 按照先序原则(自己是根,它的下一位按照 左孩子 右孩子 的方式)接着推下一位元素。
TreeNode* getNext(TreeNode* node) //线性表
{
if (node->rtag == 1) // 如果它没有右孩子
{
return node->rChild;//就返回它的后继元素
}
else //如果有右孩子 根据先序 根左右 先返回左孩子
{
if (node->ltag == 0)// 有左孩子
{
return node->lChild;//返回左孩子
}
else // 没有左孩子 根据 先序根左右 应该返回右孩子了
{
return node->rChild;//返回右孩子
}
}
}五、用for循环遍历打印
例如 将 A B D E C 一个一个输出。 node = 根结点A,进行打印,再使node 变成 下一个元素 B ,进行打印...直到node == NULL。
for (TreeNode* node = T; node != NULL; node = getNext(node))
{
printf("%c ", node->data);
}
printf("\n");主函数中:
需将最后一个元素主动更改,使它的rtag = 1,并将指向右孩子改为指向NULL;
int main()
{
TreeNode* T = creatTree();
TreeNode* pre= NULL;
preThreadTree(T, &pre);
pre->rtag = 1; //最后的线性结点指向NULL
pre->rChild = NULL;
for (TreeNode* node = T; node != NULL; node = getNext(node))
{
printf("%c ", node->data);
}
printf("\n");
return 0;
}六、完整代码
#include
#include
typedef struct TreeNode
{
int ltag, rtag;
char data;
struct TreeNode* lChild;
struct TreeNode* rChild;
}TreeNode;
//初始化
TreeNode* creatTree()
{
TreeNode* T;
char ch;
scanf_s("%c", &ch);//通过输入的ch是否是‘#’来判断该节点是否有孩子节点
if (ch == '#')
{
//为空结点
return NULL;
}
else
{
T = (TreeNode*)malloc(sizeof(TreeNode));
T->data = ch;
T->ltag = 0;
T->rtag = 0;
printf("");
T->lChild = creatTree();
T->rChild = creatTree();
return T;
}
}
void preThreadTree(TreeNode* T, TreeNode** pre)
{
if (T)//传进来的结点是否为空
{
if (T->lChild == NULL) //左孩子为空 指向前驱 假设当前为树结点 为 A
{
T->ltag = 1; //标记为1
T->lChild = *pre; //A的左孩子指向前驱元素 假设当前 前驱元素为B
}
if (*pre != NULL && (*pre)->rChild == NULL)//前驱元素B不为空 且 它的右孩子为空 指向后继元素 A
{
(*pre)->rtag = 1;//标记为1
(*pre)->rChild = T; //B的右孩子 指向 后继元素A
}
*pre = T;
if (T->ltag == 0)//如果有左孩子
{
preThreadTree(T->lChild, pre);//指向左孩子
}
preThreadTree(T->rChild, pre);//指向右孩子
}
}
TreeNode* getNext(TreeNode* node) //线性表
{
if (node->rtag == 1) // 如果它没有右孩子
{
return node->rChild;//就返回它的后继元素
}
else //如果有右孩子 根据先序 根左右 先返回左孩子
{
if (node->ltag == 0)// 有左孩子
{
return node->lChild;//返回左孩子
}
else // 没有左孩子 根据 先序根左右 应该返回右孩子了
{
return node->rChild;//返回右孩子
}
}
}
int main()
{
TreeNode* T = creatTree();
TreeNode* pre= NULL;
preThreadTree(T, &pre);
pre->rtag = 1; //最后的线性结点指向NULL
pre->rChild = NULL;
for (TreeNode* node = T; node != NULL; node = getNext(node))
{
printf("%c ", node->data);
}
printf("\n");
return 0;
} 七、运行结果
输入ABD##E##C##
总结:
线索二叉树的好处在于它能够提高二叉树的遍历效率。传统的二叉树遍历方式,如先序遍历、中序遍历、后序遍历,需要通过递归或循环遍历整棵二叉树,而在线索二叉树中,每个节点都含有指向其前驱和后继节点的线索信息,因此可以直接访问每个节点的前驱和后继节点,从而不需要进行递归或循环遍历,大大提高了遍历的效率。
制作不易,真心想让你懂,还是有不足的地方,望见谅嘞。