力扣刷题day3(移除元素,找出字符串中的第一个不匹配项的下标,搜索插入位置)
题目1:27.移除元素
思路1和代码:
//由于题目要求删除数组中等于 val\textit{ val }val 的元素,因此输出数组的长度一定小于等于输入数组的长度,我们可以把输出的数组直接写在输入数组上。可以使用双指针:右指针 right\textit{ right }right 指向当前将要处理的元素,左指针 left\textit{ left }left 指向下一个将要赋值的位置。
//
//如果右指针指向的元素不等于 val\textit{ val }val,它一定是输出数组的一个元素,我们就将右指针指向的元素复制到左指针位置,然后将左右指针同时右移;
//
//如果右指针指向的元素等于 val\textit{ val }val,它不能在输出数组里,此时左指针不动,右指针右移一位。
//
//整个过程保持不变的性质是:区间[0, left)[0, \textit{ left })[0, left) 中的元素都不等于 val\textit{ val }val。当左右指针遍历完输入数组以后,left\textit{ left }left 的值就是输出数组的长度。
//
//这样的算法在最坏情况下(输入数组中没有元素等于 val\textit{ val }val),左右指针各遍历了数组一次。
出处:力扣官方
int removeElement(int* nums, int numsSize, int val)
{
int left = 0; // 定义左指针
for (int right = 0; right < numsSize; right++) // 遍历数组
{
if (nums[right] != val) // 如果当前元素不等于要移除的值
{
nums[left] = nums[right]; // 将当前元素移动到左指针位置
left++; // 左指针右移
}
}
return left; // 返回最终的左指针位置
}思路2和代码:
//双指针优化
//思路
//
//如果要移除的元素恰好在数组的开头,例如序列[1, 2, 3, 4, 5][1, 2, 3, 4, 5][1, 2, 3, 4, 5],当 val\textit{ val }val 为 111 时,我们需要把每一个元素都左移一位。注意到题目中说:「元素的顺序可以改变」。实际上我们可以直接将最后一个元素 555 移动到序列开头,取代元素 111,得到序列[5, 2, 3, 4][5, 2, 3, 4][5, 2, 3, 4],同样满足题目要求。这个优化在序列中 val\textit{ val }val 元素的数量较少时非常有效。
//
//实现方面,我们依然使用双指针,两个指针初始时分别位于数组的首尾,向中间移动遍历该序列。
//
//算法
//
//如果左指针 left\textit{ left }left 指向的元素等于 val\textit{ val }val,此时将右指针 right\textit{ right }right 指向的元素复制到左指针 left\textit{ left }left 的位置,然后右指针 right\textit{ right }right 左移一位。如果赋值过来的元素恰好也等于 val\textit{ val }val,可以继续把右指针 right\textit{ right }right 指向的元素的值赋值过来(左指针 left\textit{ left }left 指向的等于 val\textit{ val }val 的元素的位置继续被覆盖),直到左指针指向的元素的值不等于 val\textit{ val }val 为止。
//
//当左指针 left\textit{ left }left 和右指针 right\textit{ right }right 重合的时候,左右指针遍历完数组中所有的元素。
//
//这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。与方法一不同的是,方法二避免了需要保留的元素的重复赋值操作。
出处:力扣官方
int removeElement(int* nums, int numsSize, int val)
{
int left = 0, right = numsSize; // 定义左右指针
while (left < right) // 当左指针小于右指针时循环
{
if (nums[left] == val) // 如果左指针指向的元素等于要移除的值
{
nums[left] = nums[right - 1]; // 将左指针指向的元素替换为右指针指向的元素
right--; // 右指针左移
}
else
{
left++; // 否则左指针右移
}
}
return left; // 返回最终的左指针位置
}题目2:28. 找出字符串中第一个匹配项的下标
思路和代码:
//找出字符串中的第一个匹配项的下标
//假设题意是叫你在排序数组中寻找是否存在一个目标值,那么训练有素的读者肯定立马就能想到利用二分法在 O(log?n)O(\log n)O(logn) 的时间内找到是否存在目标值。但这题还多了个额外的条件,即如果不存在数组中的时候需要返回按顺序插入的位置,那我们还能用二分法么?答案是可以的,我们只需要稍作修改即可。
//
//考虑这个插入的位置 pos\textit{ pos }pos,它成立的条件为:
//
//nums[pos?1] < target≤nums[pos]\textit{ nums }[pos - 1] < \textit{ target }\le \textit{ nums }[pos]
// nums[pos?1] < target≤nums[pos]
// 其中 nums\textit{ nums }nums 代表排序数组。由于如果存在这个目标值,我们返回的索引也是 pos\textit{ pos }pos,因此我们可以将两个条件合并得出最后的目标:「在一个有序数组中找第一个大于等于 target\textit{ target }target 的下标」。
//
// 问题转化到这里,直接套用二分法即可,即不断用二分法逼近查找第一个大于等于 target\textit{ target }target 的下标 。下文给出的代码是笔者习惯的二分写法,ans\textit{ ans }ans 初值设置为数组长度可以省略边界条件的判断,因为存在一种情况是 target\textit{ target }target 大于数组中的所有数,此时需要插入到数组长度的位置。
//int strStr(char* haystack, char* needle)
出处:力扣官方
int strStr(char* haystack, char* needle)
{
int n = strlen(haystack), m = strlen(needle); // 获取 haystack 和 needle 的长度
for (int i = 0; i + m <= n; i++) // 遍历 haystack
{
bool flag = true; // 设置标志位为真
for (int j = 0; j < m; j++) // 遍历 needle
{
if (haystack[i + j] != needle[j]) // 检查当前位置的字符是否匹配
{
flag = false; // 若不匹配,则将标志位置为假,并跳出循环
break;
}
}
if (flag)
{ // 如果标志位仍为真,说明找到了匹配的子串,返回起始位置
return i;
}
}
return -1; // 遍历完 haystack 后仍未找到匹配的子串,返回 -1
}题目3:35. 搜索插入位置
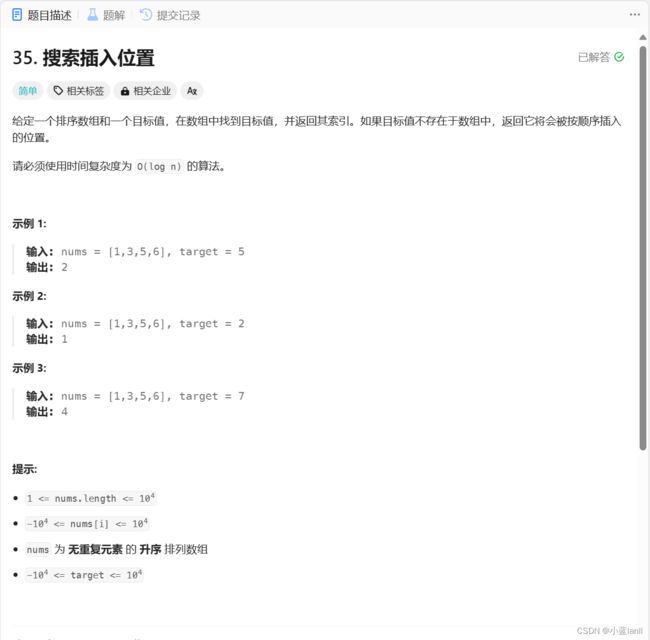 思路和代码:
思路和代码:
//搜索插入位置
int searchInsert(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize - 1; // 初始化左右指针
while (left <= right) // 当左指针小于等于右指针时循环
{
int mid = (left + right) / 2; // 计算中间位置
if (nums[mid] == target) // 如果中间元素等于目标值
return mid; // 返回中间位置
else if (nums[mid] > target) // 如果中间元素大于目标值
right = mid - 1; // 将右指针移到中间位置的左边
else if (nums[mid] < target) // 如果中间元素小于目标值
left = mid + 1; // 将左指针移到中间位置的右边
}
return left; // 返回左指针位置
}

