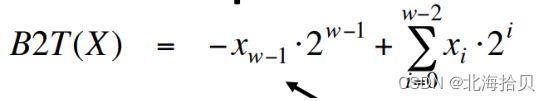《深入理解计算机系统》学习笔记 - 第三课 - 位，字节和整型
Lecture 03 Bits,Bytes, and Integer count 位，字节，整型
文章目录
- Lecture 03 Bits,Bytes, and Integer count 位，字节，整型
-
- 运算：加，减，乘，除
-
- 加法
- 乘法
-
- 取值范围
- 乘法结果
- 使用无符号注意事项
- 内存中的表现形式
-
- 面向字节的内存组织形式
- 字长 Words
- 字节顺序
-
- 大端序和小端序
- 代码检验数据的表现形式
- 字符串表示
- 拓展
-
- 二进制的一个属性
- 汇编编码
-
- 乘积编码
- 除法编码
-
- 无符号除法编码
- 有符号除法编码
- 读字节倒转清单
- 问题
-
- 为什么十进制使用普遍？
- 为什么用最高位作为符号位？
- 《深入理解计算机系统》书籍学习笔记
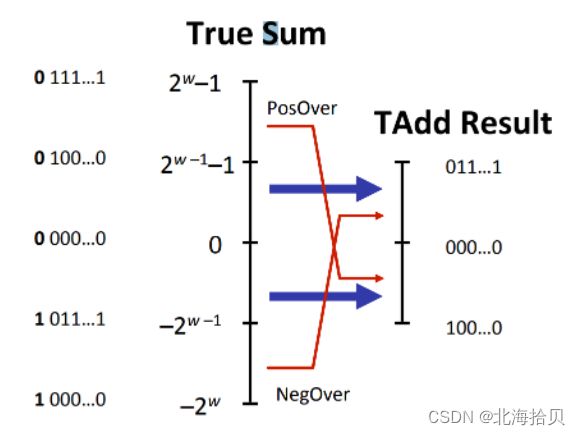
运算：加，减，乘，除
主要运算导致溢出的情况。
都是截去超出w位的高位值。
加法
-
无符号加法
操作两个w位相加，结果w+1位。
u + v = (u + v) mod 2^w -
有符号加法
操作两个w位相加，结果w+1位。
溢出的部分截去。
乘法
取值范围
w 位的数的乘法结果的范围：
最高2w 位。
-
无符号
范围：0 <= x * y <= (2^w - 1)^2 = 2^(2w) - 2^(w+1) + 1 -
二进制补码
范围：
最小值： xy >= (-2^(w-1)) * (2^(w-1) -1) = -2^(2s-2) + 2^(w-1)
最大值(TMin)^2：xy <= (-2(w-1))2 = 2^(2w-2)
乘法结果
- 无符号位
截去高序w位的值，也就是结果模2^w。
UMult(u,v) = u * v mod 2^w
-
有符号位
截去高序w位的值。 -
2的幂的乘积与位移的关系
左移几位就是乘以2的几次幂。
u << k = u * 2^k
- 无符号除法与位移关系
右移几位，就是除以2的几次幂
u >> k = u / 2^k
使用无符号注意事项
无符号数绝对不会出现负值的情况。
#include
#include
void main() {
unsigned i;
int cnt = 5;
for (i = cnt - 2; i >= 0; i--) {
usleep(100000);
printf("%d,%u\n", i,i);
}
}
// output:
// 3,3
// 2,2
// 1,1
// 0,0
// -1,4294967295
// -2,4294967294
// -3,4294967293
// ....
程序将陷入死循环。
因为无符号永远大于0.
#include
#include
void main() {
#define DELTA sizeof(int)
int i;
int cnt = 10;
for (i = cnt; i-DELTA >= 0; i-= DELTA) {
usleep(100000);
printf("%d\n",i);
}
}
// output:
// 10
// 6
// 2
// -2
// -6
// -10
// ...
解决无符号循环问题：
使用总数作为终止判断条件，而不是0.
void main() {
unsigned i;
int cnt = 5;
for (i = cnt-2; i < cnt; i--) {
printf("%d\n",i);
}
}
内存中的表现形式
面向字节的内存组织形式
- 程序通过地址指向数据
从概念上讲，可以把它想象成一个非常大的字节数组。当然实际并非如此。 - 地址就像数组的索引
指针变量存储地址。
注意：系统给每个进程分配私有的地址空间。
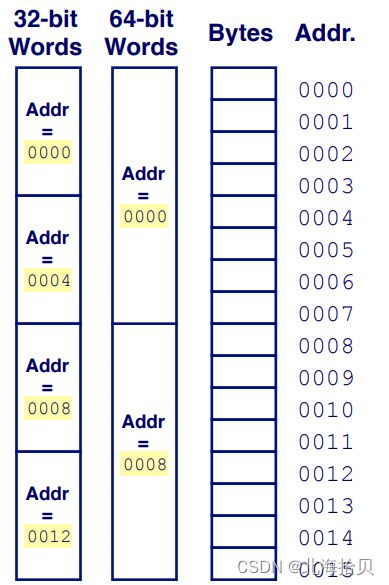
字长 Words
面向字节内存组织方式
32位的四个字节，64位的八个字节。
字节顺序
大端序：最低有效位字节具有最高地址
小端序：最低有效位字节具有最低地址
4字节的值：0x01234567
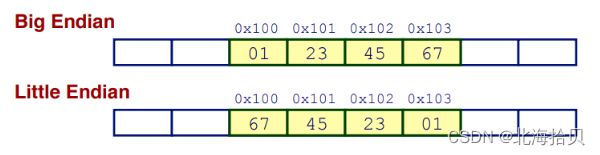
大端序和小端序
现在几乎都是小端序。
大端序：人类更容易识别。
但是对于机器来说，无所谓，只要有统一标准就行。
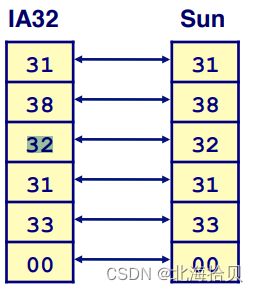
代码检验数据的表现形式
指向unsigned char *的指针允许作为字节数组处理
#include
typedef unsigned char *pointer;
void show_bytes(pointer start, size_t len) {
size_t i;
for (i = 0; i < len; i++)
printf("%p\t0x%.2x\n", start+i, start[i]);
printf("\n");
}
void main() {
int a= 15213;
printf("int a = 15213;\n");
show_bytes((pointer) &a, sizeof(int));
}
// output:
// int a = 15213;
// 0x7ffc2881f59c 0x6d
// 0x7ffc2881f59d 0x3b
// 0x7ffc2881f59e 0x00
// 0x7ffc2881f59f 0x00
字符串表示
- 用字符数组表示。
- 每个字符使用ASCII格式编码
- 字符集的标准7位编码
- 字符0 使用 0x30 编码
数字i 使用 ox30 + i 表示
- 字符应该有空终止符
使用字符0
char S[6] = "18213" 编码：
拓展
二进制的一个属性
1 + 1 + 2 + 4 + 8 + … + 2^(w-1) = 2^w
得出：
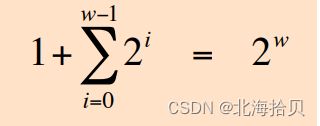
汇编编码
乘积编码
- 乘积代码
文件mul12.c:
long mul12(long x)
{
return x*12;
}
- 汇编代码
生成汇编代码：gcc -O2 -S mul12.c
汇编文件mul12.s:
leaq (%rax, %rax, 2), %rax // t <- x + x*2
sqlq $2, %rax // return t << 2;
除法编码
无符号除法编码
- 除法代码
unsigned long udiv8(unsigned long x) {
return x/8;
}
- 汇编代码
生成汇编代码：gcc -O2 -S udiv8.c
汇编文件udiv8.s:
shrq $3, $rax // return x >> 3;
有符号除法编码
与无符号类似，不过结果需要加1。
- 除法代码
long udiv8(unsigned long x) {
return x/8;
}
- 汇编代码
生成汇编代码：gcc -O2 -S udiv8.c
汇编文件udiv8.s:
testq %rax, %rax // if x < 0
js L4
L3:
shrq $3, $rax // x >> 3;
ret // ret
L4:
addq %7, %rax // x += 7
jmp L3
读字节倒转清单
按小端序读取：
问题
为什么十进制使用普遍？
因为人们有十个手指头。
为什么用最高位作为符号位？
我们看下二进制转化为有符号数公式：
满足了符号数以下特征：
整数负数各一半。
再问为什么不直接用符号位来表示正负数?
下面这种表示方式：
1001
= -1*(2^0) = -1
不利于无符号有符号的转换。
当然，主要这种情况可以满足所有情况了，我们没有必要再考虑去推翻它，这个没有必然的合理优势的话是不可能推翻的。
《深入理解计算机系统》书籍学习笔记
《深入理解计算机系统》学习笔记 - 第一课 - 课程简介
《深入理解计算机系统》学习笔记 - 第二课 - 位，字节和整型
《深入理解计算机系统》学习笔记 - 第三课 - 位，字节和整型
《深入理解计算机系统》学习笔记 - 第四课 - 浮点数
《深入理解计算机系统》学习笔记 - 第四课 - 机器级别的程序