代码随想录算法训练营第三天 | 双指针、滑动窗口

目录

力扣题目

链表理论基础 

链表的定义

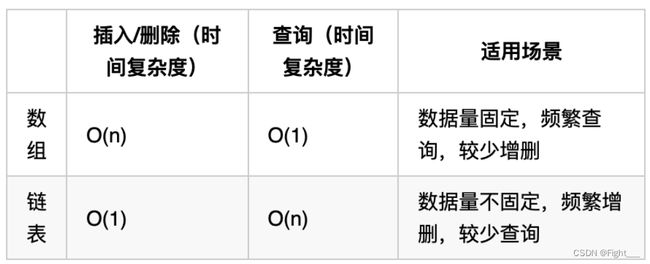
性能分析

力扣题目记录

203.移除链表元素

707.设计链表

206.反转链表

双指针法（常规）

递归法（需要二刷）

双指针法（从后向前）（需要二刷）

使用虚拟头结点解决链表反转（需要二刷）

使用栈解决反转链表的问题（需要二刷）

总结

---

力扣题目

用时：2.5h

1、203.移除链表元素

2、707.设计链表

3、206.反转链表（重点，方法很多）

---

链表理论基础 

链表的定义

// 单链表
struct ListNode {
    int val;  // 节点上存储的元素
    ListNode *next;  // 指向下一个节点的指针
    ListNode(int x) : val(x), next(NULL) {}  // 节点的构造函数
};

也可以不写构造函数，C++默认生成一个构造函数。

但是这个构造函数不会初始化任何成员变量，比如：

通过自己定义构造函数初始化节点：

ListNode* head = new ListNode(5);

使用默认构造函数初始化节点：

ListNode* head = new ListNode();
head->val = 5;

所以如果不定义构造函数使用默认构造函数的话，在初始化的时候就不能直接给变量赋值！

性能分析

---

力扣题目记录

203.移除链表元素

这个题不难，但是涉及如下链表操作的两种方式：

• 直接使用原来的链表来进行删除操作。
• 设置一个虚拟头结点在进行删除操作。

直接使用原来的链表来进行移除节点操作：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        // 删除头结点
        while (head != NULL && head->val == val) { // 注意这里不是if
            ListNode* tmp = head;
            head = head->next;
            delete tmp;
        }

        // 删除非头结点
        ListNode* cur = head;
        while (cur != NULL && cur->next!= NULL) {
            if (cur->next->val == val) {
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            } else {
                cur = cur->next;
            }
        }
        return head;
    }
};

设置一个虚拟头结点在进行移除节点操作：

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方便后面做删除操作
        ListNode* cur = dummyHead;
        while (cur->next != NULL) {
            if(cur->next->val == val) {
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            } else {
                cur = cur->next;
            }
        }
        head = dummyHead->next;
        delete dummyHead;
        return head;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1)

---

707.设计链表

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };

    // 初始化链表
    MyLinkedList() {
        _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点，而不是真正的链表头结点
        _size = 0;
    }

    // 获取到第index个节点数值，如果index是非法数值直接返回-1， 注意index是从0开始的，第0个节点就是头结点
    int get(int index) {
        if (index > (_size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = _dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    // 在链表最前面插入一个节点，插入完成后，新插入的节点为链表的新的头结点
    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = _dummyHead->next;
        _dummyHead->next = newNode;
        _size++;
    }

    // 在链表最后面添加一个节点
    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        _size++;
    }

    // 在第index个节点之前插入一个新节点，例如index为0，那么新插入的节点为链表的新头节点。
    // 如果index 等于链表的长度，则说明是新插入的节点为链表的尾结点
    // 如果index大于链表的长度，则返回空
    // 如果index小于0，则在头部插入节点
    void addAtIndex(int index, int val) {

        if(index > _size) return;
        if(index < 0) index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        _size++;
    }

    // 删除第index个节点，如果index 大于等于链表的长度，直接return，注意index是从0开始的
    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = _dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        //delete命令指示释放了tmp指针原本所指的那部分内存，
        //被delete后的指针tmp的值（地址）并非就是NULL，而是随机值。也就是被delete后，
        //如果不再加上一句tmp=nullptr,tmp会成为乱指的野指针
        //如果之后的程序不小心使用了tmp，会指向难以预想的内存空间
        tmp=nullptr;
        _size--;
    }

    // 打印链表
    void printLinkedList() {
        LinkedNode* cur = _dummyHead;
        while (cur->next != nullptr) {
            cout << cur->next->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
private:
    int _size;
    LinkedNode* _dummyHead;

};

---

206.反转链表

如果再定义一个新的链表，实现链表元素的反转，其实这是对内存空间的浪费。

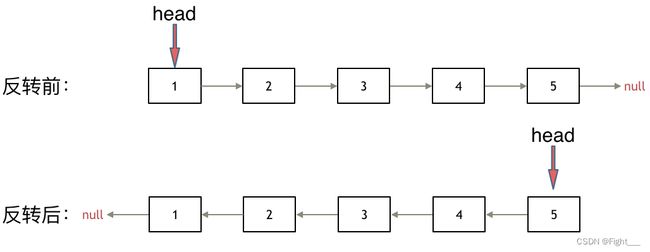
其实只需要改变链表的next指针的指向，直接将链表反转 ，而不用重新定义一个新的链表，如图所示:

首先定义一个cur指针，指向头结点，再定义一个pre指针，初始化为null。

然后就要开始反转了，首先要把 cur->next 节点用tmp指针保存一下，也就是保存一下这个节点。

为什么要保存一下这个节点呢，因为接下来要改变 cur->next 的指向了，将cur->next 指向pre ，此时已经反转了第一个节点了。

接下来，就是循环走如下代码逻辑了，继续移动pre和cur指针。

最后，cur 指针已经指向了null，循环结束，链表也反转完毕了。 此时我们return pre指针就可以了，pre指针就指向了新的头结点。

双指针法（常规）

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* temp; // 保存cur的下一个节点
        ListNode* cur = head;
        ListNode* pre = NULL;
        while(cur) {
            temp = cur->next;  // 保存一下 cur的下一个节点，因为接下来要改变cur->next
            cur->next = pre; // 翻转操作
            // 更新pre 和 cur指针
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1)

递归法（需要二刷）

归法相对抽象一些，但是其实和双指针法是一样的逻辑，同样是当cur为空的时候循环结束，不断将cur指向pre的过程。

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        // 可以和双指针法的代码进行对比，如下递归的写法，其实就是做了这两步
        // pre = cur;
        // cur = temp;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        // 和双指针法初始化是一样的逻辑
        // ListNode* cur = head;
        // ListNode* pre = NULL;
        return reverse(NULL, head);
    }

};

• 时间复杂度: O(n), 要递归处理链表的每个节点
• 空间复杂度: O(n), 递归调用了 n 层栈空间

双指针法（从后向前）（需要二刷）

我们可以发现，上面的递归写法和双指针法实质上都是从前往后翻转指针指向，其实还有另外一种与双指针法不同思路的递归写法：从后往前翻转指针指向。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        // 边缘条件判断
        if(head == NULL) return NULL;
        if (head->next == NULL) return head;
        
        // 递归调用，翻转第二个节点开始往后的链表
        ListNode *last = reverseList(head->next);
        // 翻转头节点与第二个节点的指向
        head->next->next = head;
        // 此时的 head 节点为尾节点，next 需要指向 NULL
        head->next = NULL;
        return last;
    }
}; 

• 时间复杂度: O(n)
• 空间复杂度: O(n)

使用虚拟头结点解决链表反转（需要二刷）

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* dummyHead = new ListNode(-1);
        dummyHead->next = NULL;

        //遍历所有节点
        ListNode* cur = head;
        while (cur != NULL)
        {
            ListNode* temp = cur->next;
            //头插法
            cur->next = dummHead->next;
            dummtHead->next = cur;
            cur = temp;
        }
        
        return dummyHead->next;
    }
};

使用栈解决反转链表的问题（需要二刷）

1. 首先将所有的结点入栈
2. 然后创建一个虚拟虚拟头结点，让cur指向虚拟头结点。然后开始循环出栈，每出来一个元素，就把它加入到以虚拟头结点为头结点的链表当中，最后返回即可。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        stack stack;
        ListNode* cur = head;
        while(cur != NULL)
        {
            stack.push(cur);
            cur = cur->next;
        }

        ListNode* pHead = new ListNode(0);
        cur = pHead;
        while (!stack.empty())
        {
            ListNode* node = stack.top();
            stack.pop();
            cur->next = node;
            cur = cur->next;
        }
        //最后一个元素的next要赋值为空
        cur->next = NULL;
        return pHead->next;
    }
};

 采用这种方法需要注意一点。就是当整个出栈循环结束以后，cur正好指向原来链表的第一个结点，而此时结点1中的next指向的是结点2，因此最后还需要cur->next = NULL

---

总结

        太久没复习链表了，以至于有些基础知识都已经忘了。在记起来知识点之后第一题和第二题就比较简单。第三题又是双指针的妙用，因为要求反序，有规律，所以可以使用双指针。除此之外，也可以用后进先出的栈。递归还是短板，下次二刷，以及有一些不是那么常规的思路，都留到二刷吧。