C语言实现哈夫曼树

哈夫曼树

在学习哈夫曼树之前，先了解以下几个概念：

一：路径长度：在一棵树中，从一个节点到另一个节点所经过的“边”的数量，被我们称为两个节点之间的路径长度。

二：树的路径长度：这是指从树根到每一个节点的路径长度的总和对于节点数相同的树来说，路径长度最短的是完全二叉树。

三：节点带权的路径长度：这是指树的根节点到该节点的路径长度和该节点权重的乘积。

四：树的带权路径长度：在一棵树中，所有叶子节点的带权路径长度之和，被称为树的带权路径长度，也被简称为WPL，这是每一个节点的对应的权值乘以对应的路径长度之和。

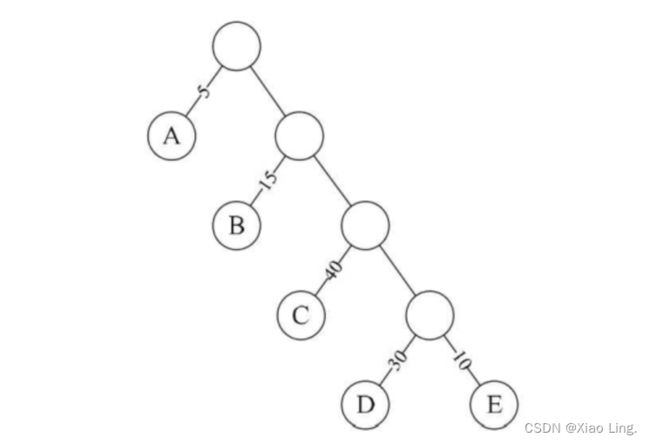
如图所示：

对于该图：

树路径长度就为1+1+2+2+3+3+4+4=20

A节点带权的路径长度=1*5=5

树的带权路径长度WPL=5×1+15×2+40×3+30×4+10×4=315

我们可以试想，同样的两颗二叉树，一个WPL小，一个WPL大，那么小的一定会在性能上优于大的，所以我们引出另外一个名词——哈夫曼树，即WPL最小的二叉树。

那我们如何才知道一棵树是不是哈夫曼树呢？且看下文：

构造哈夫曼树:

1. 首先，假如我们有5个节点，它们的权值分别是：A5, E10, B15, D30, C40。

2. 在这些节点中，我们找到权值最小的两个节点，这里是A5和E10。我们将这两个节点合并，生成一个新的节点，新节点的权值是A5和E10的权值之和，即15。这样，我们就得到了新的节点列表：AE15, B15, D30, C40。

3. 我们再次在新的节点列表中找到权值最小的两个节点，这次是AE15和B15。我们将这两个节点合并，生成一个新的节点，新节点的权值是AE15和B15的权值之和，即30。这样，我们就得到了新的节点列表：AEB30, D30, C40。

4. 我们继续在新的节点列表中找到权值最小的两个节点，这次是AEB30和D30。我们将这两个节点合并，生成一个新的节点，新节点的权值是AEB30和D30的权值之和，即60。这样，我们就得到了新的节点列表：AEBD60, C40。

5. 最后，我们将剩下的两个节点合并，生成一个新的节点，新节点的权值是AEBD60和C40的权值之和，即100。这样，我们就得到了最终的哈夫曼树。

比如这两个图，就是第一步的操作的举例：

当完成后，我们只需要比较一下当前WPL和我们的WPL，如相等，则就是哈夫曼树。

对于一颗哈夫曼树，有：

• 哈夫曼树中权越大的叶子离根越近
• 具有相同带权结点的哈夫曼树不唯一
• 哈夫曼树只有度为0或2的结点，没有度为1的结点
• 包含n个叶子结点的哈夫曼树共有2n-1个结点(如上图，叶子节点为3，总共2*3-1==5个节点)
• n棵二叉树要经历n-1次合并可以形成哈夫曼树

哈夫曼编码：

哈夫曼编码是一种用于无损数据压缩的熵编码（即编码效率最高）算法。它是一种可变字长编码方式，比起定长编码的ASCII编码来说，哈夫曼编码能节省很多的空间，因为每一个字符出现的频率不是一致的。

哈夫曼编码的基本原理和流程如下：

1. 将字符集C作为叶子节点；
2. 将频率集W作为叶子节点的权值；
3. 使用C和W构造哈夫曼树；
4. 对哈夫曼树的所有分支，左子树分支编码为0，右子树分支编码为1；
5. 通过上述流程，即完成了哈夫曼编码。

下面我们来用代码实现一颗哈夫曼树：

首先是结构体的定义：

struct haftree {
	double weight;//节点权值
	char c;//节点名字
	int lchild, rchild, parent;
};

接下来是各个函数的定义：

1.找出各权值中最小的两个：

void selcet(struct haftree* array, int x, int* m1, int* m2) {
	double min1 = DBL_MAX;
	double min2 = DBL_MAX;
	for (int i = 1; i <= x; i++) {
		if (array[i].weight < min1 && array[i].parent == 0) {//在构建哈夫曼树的过程  //中，我们需要选择权重最小的两个结点进行合并，构建出新的结点。为了避免重复选择已经合并过的结点， //我们需要在选择最小权重结点的时候排除已经合并的结点。因此，需要通过array[i].parent == 0来判 //断结点是否已经是其他结点的子结点，如果是，则不考虑这个结点。
			min1 = array[i].weight;
			*m1 = i;
		}
	}
	for (int j = 1; j <= x; j++) {
		if (array[j].weight < min2 && j != *m1 && array[j].parent == 0) {
			min2 = array[j].weight;
			*m2 = j;
		}
	}
}

2.构建哈夫曼树：

void createhaftree(struct haftree*array,int n) {
	for (int i = n + 1; i <= 2 * n - 1; i++) {
		int m1,m2;
		Select(array, i - 1, &m1, &m2);
		array[i].weight = array[m1].weight + array[m2].weight;
		array[i].lchild = m1;
		array[i].rchild = m2;
		array[m1].parent = i;
		array[m2].parent = i;
	}
}

3.哈夫曼编码：

void HuffmanCoding(struct haftree* array, int n) {
	char cd[n + 1];
	int start;
	cd[n] = '\0';
	for (int i = 1; i <= n; i++) {
		start = n;
		int c = i;
		int f = array[i].parent;
		while (f != 0) {
			if (array[f].lchild == c)
				cd[--start] = '0';
			else
				cd[--start] = '1';
			c = f;
			f = array[f].parent;
		}
		printf("%s\n", &cd[start]);
	}
}

解释如下：

1. void HuffmanCoding(struct haftree* array, int n): 这是一个函数定义，函数名为HuffmanCoding，它接受一个haftree结构体数组和一个整数n作为参数。haftree是一个自定义的数据结构，用于存储哈夫曼树的节点。
2. char cd[n + 1]; int start; cd[n] = '\0';: 这里定义了一个字符数组cd，长度为n+1，并将最后一个元素设为终止符'\0'。start是一个整数，用于记录当前编码的起始位置。
3. for (int i = 1; i <= n; i++): 这是一个循环，对haftree数组中的每个元素进行操作。
4. start = n; int c = i; int f = array[i].parent;: 在每次循环开始时，将start设为n，c设为当前循环的索引i，f设为当前元素的父节点。
5. while (f != 0): 这是一个循环，用于生成从叶子节点到根节点的哈夫曼编码。
6. if (array[f].lchild == c) cd[--start] = '0'; else cd[--start] = '1';: 如果当前节点是其父节点的左孩子，则编码为0，否则编码为1。
7. c = f; f = array[f].parent;: 更新当前节点和父节点。
8. printf("%s\n", &cd[start]);: 打印生成的哈夫曼编码。

总的来说，这段代码实现了哈夫曼编码的生成，它从每个叶子节点开始，沿着到根节点的路径生成编码，然后打印出来。

4.初始化与预处理：

for (int i = 1; i <= n; i++) {
	array[i].weight = weights[i - 1];
	array[i].c = chars[i - 1];
	array[i].parent = 0;
	array[i].lchild = 0;
	array[i].rchild = 0;
}
// 初始化非叶子节点
for (int i = n + 1; i < 2 * n; i++) {
	array[i].weight = 0;
	array[i].c = '\0'; // 非叶子节点没有字符
	array[i].parent = 0;
	array[i].lchild = 0;
	array[i].rchild = 0;
}

完整代码如下：

#include 
#include 
#include 
struct haftree {
	double weight;//节点权值
	char c;//节点名字
	int lchild, rchild, parent;
};
void Select(struct haftree* array, int x, int* m1, int* m2) {
	double min1 = DBL_MAX;
	double min2 = DBL_MAX;
	for (int i = 1; i <= x; i++) {
		if (array[i].weight < min1 && array[i].parent == 0) {
			min1 = array[i].weight;
			*m1 = i;
		}
	}
	for (int j = 1; j <= x; j++) {
		if (array[j].weight < min2 && j != *m1 && array[j].parent == 0) {
			min2 = array[j].weight;
			*m2 = j;
		}
	}
}
void createhaftree(struct haftree* array, int n) {
	for (int i = n + 1; i <= 2 * n - 1; i++) {
		int m1, m2;
		Select(array, i - 1, &m1, &m2);
		array[i].weight = array[m1].weight + array[m2].weight;
		array[i].lchild = m1;
		array[i].rchild = m2;
		array[m1].parent = i;
		array[m2].parent = i;
	}
}
void HuffmanCoding(struct haftree* array, int n) {
	char cd[n + 1];
	int start;
	cd[n] = '\0';
	for (int i = 1; i <= n; i++) {
		start = n;
		int c = i;
		int f = array[i].parent;
		while (f != 0) {
			if (array[f].lchild == c)
				cd[--start] = '0';
			else
				cd[--start] = '1';
			c = f;
			f = array[f].parent;
		}
		printf("%s\n", &cd[start]);
	}
}
int main() {
	int n = 5; // 假设有5个字符
	struct haftree array[2 * n]; // 创建哈夫曼树数组
	double weights[] = { 0.1, 0.15, 0.2, 0.25, 0.3 }; // 假设这是每个字符的权重
	char chars[] = { 'a', 'b', 'c', 'd', 'e' }; // 这是每个字符
// 初始化叶子节点
for (int i = 1; i <= n; i++) {
	array[i].weight = weights[i - 1];
	array[i].c = chars[i - 1];
	array[i].parent = 0;
	array[i].lchild = 0;
	array[i].rchild = 0;
}
// 初始化非叶子节点
for (int i = n + 1; i < 2 * n; i++) {
	array[i].weight = 0;
	array[i].c = '\0'; // 非叶子节点没有字符
	array[i].parent = 0;
	array[i].lchild = 0;
	array[i].rchild = 0;
}
createhaftree(array, n);
HuffmanCoding(array, n);
return 0;
}