【Shuffle Attention】《SA-Net:Shuffle Attention for Deep Convolutional Neural Networks》
ICASSP-2021
文章目录
- 1 Background and Motivation
- 2 Related Work
- 3 Advantages / Contributions
- 4 Method
- 5 Experiments
-
- 5.1 Datasets and Metrics
- 5.2 Classification on ImageNet-1k
- 5.3 Ablation Study
- 5.4 Object Detection on MSCOCO
- 5.5 Instance Segmentation on MS COCO
- 5.6 Visualization and Interpretation
- 6 Conclusion(own)
1 Background and Motivation
CNN 中注意力是一个很有效的提点方式,一般可分为通道注意力和空间注意力,也有二合一的,但往往 suffered from either converging difficulty or heavy computation burdens.
“Can one fuse different attention modules in a lighter but more efficient way?”
作者基于此提出 Shuffle Attention,轻量高效
2 Related Work
- Multi-branch architectures
Inception / ResNet / SKNet / ShuffleNets - Grouped Features
AlexNet / MobileNets / ShuffleNets / CapsuleNets / SGE - Attention mechanisms
SE / SGE / ECA-Net / GCNet / Non-Local / CBAM / DA
3 Advantages / Contributions
提出 shuffle attention,基本无参,ImageNet-1k for classification, MS COCO for object detection, and instance segmentation 上提点明显
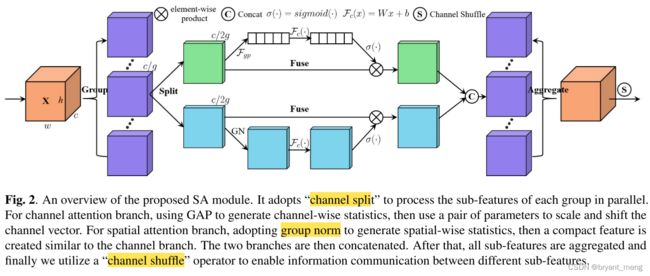
4 Method
(1)Feature Grouping
X ∈ R C × H × W X \in \mathbb{R}^{C \times H \times W} X∈RC×H×W
分成 G G G 组, X = [ X 1 , X 2 , . . . , X G ] X = [X_1, X_2, ..., X_G] X=[X1,X2,...,XG], X k ∈ R C / G × H × W X_k \in \mathbb{R} ^{C/G \times H \times W} Xk∈RC/G×H×W
split 两个分支
X k 1 , X k 2 ∈ R C / 2 G × H × W X_{k1}, X_{k2} \in \mathbb{R} ^ {C/2G \times H \times W} Xk1,Xk2∈RC/2G×H×W
分别做通道注意力和空间注意力
(2)Channel Attention

s ∈ R C / 2 G × 1 × 1 s \in \mathbb{R} ^ {C/2G \times 1 \times 1} s∈RC/2G×1×1

W 1 ∈ R C / 2 G × 1 × 1 W_1 \in \mathbb{R} ^ {C/2G \times 1 \times 1} W1∈RC/2G×1×1
b 1 ∈ R C / 2 G × 1 × 1 b_1 \in \mathbb{R} ^ {C/2G \times 1 \times 1} b1∈RC/2G×1×1
所有组别 G 中 W 1 W_1 W1 和 b 1 b_1 b1 参数共享
(3)Spatial Attention
W 2 ∈ R C / 2 G × 1 × 1 W_2 \in \mathbb{R} ^ {C/2G \times 1 \times 1} W2∈RC/2G×1×1
b 2 ∈ R C / 2 G × 1 × 1 b_2 \in \mathbb{R} ^ {C/2G \times 1 \times 1} b2∈RC/2G×1×1
所有组别 G 中 W 2 W_2 W2 和 b 2 b_2 b2 参数共享
X k ′ = [ X k 1 ′ , X k 2 ′ ] ∈ R C / 2 G × H × W X_k^{{}'} = [X_{k_1}^{{}'}, X_{k_2}^{{}'}] \in \mathbb{R}^{C/2G \times H \times W} Xk′=[Xk1′,Xk2′]∈RC/2G×H×W
来了个组卷积以实现空间注意力,组卷积细节如下
GN 的极端情况就是 IN 和 LN
分别对应 G 等于 C 和 G 等于 1
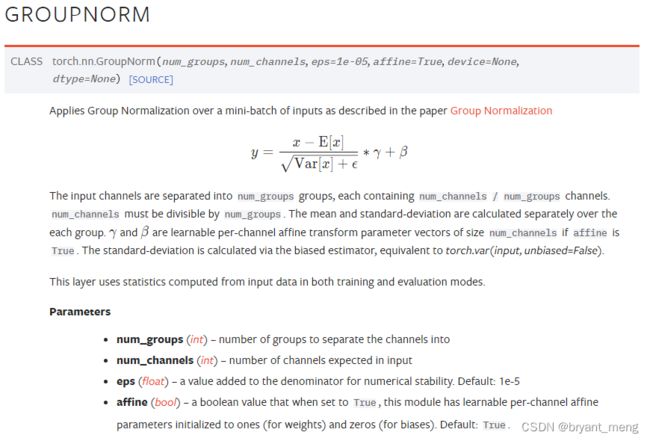
torch.nn.GroupNorm(num_groups,num_channels),将channel切分成许多组进行归一化
- num_groups:组数
- num_channels:通道数量
PyTorch学习之归一化层(BatchNorm、LayerNorm、InstanceNorm、GroupNorm)
为什么组卷积可以实现空间注意力呢,作者是这样解释的
代码中看作者的 group normal 是当 instance normal 来做的(groups 的数量同 channels),这个操作有 spatial attention 的感觉,但是乘以一个 w 再加个 b 就有点通道注意力的感觉了,最后 sigmoid 的话标配,混合了空间和通道,感觉 spatial attention 的 learning 的过程都集中在了 instance normal 层
(4)Aggregation
concat + shuffle channel
total parameters are 3 C / G 3C/G 3C/G
(5)Implementation
伪代码
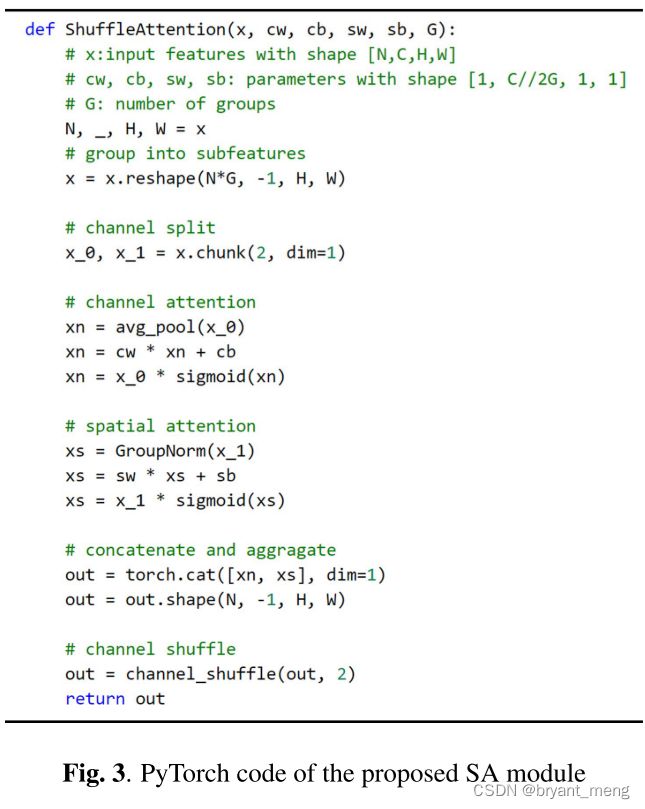
实际的代码:https://github.com/wofmanaf/SA-Net
以 (1,256,4,4) 输入 G=8 为例,写下各个流程中特征图 shape 变化情况
class sa_layer(nn.Module):
"""Constructs a Channel Spatial Group module.
Args:
k_size: Adaptive selection of kernel size
"""
def __init__(self, channel, groups=64):
super(sa_layer, self).__init__()
self.groups = groups
self.avg_pool = nn.AdaptiveAvgPool2d(1)
self.cweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1)) # (1,16,1,1)
self.cbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1)) # (1,16,1,1)
self.sweight = Parameter(torch.zeros(1, channel // (2 * groups), 1, 1)) # (1,16,1,1)
self.sbias = Parameter(torch.ones(1, channel // (2 * groups), 1, 1)) # (1,16,1,1)
self.sigmoid = nn.Sigmoid()
self.gn = nn.GroupNorm(channel // (2 * groups), channel // (2 * groups)) # 16, 16
@staticmethod
def channel_shuffle(x, groups):
b, c, h, w = x.shape # (1,256,4,4)
x = x.reshape(b, groups, -1, h, w) # (1,2,128,4,4)
x = x.permute(0, 2, 1, 3, 4) # (1,128,2,4,4)
# flatten
x = x.reshape(b, -1, h, w) # (1,256,4,4)
return x
def forward(self, x):
b, c, h, w = x.shape # (1,256,4,4)
x = x.reshape(b * self.groups, -1, h, w) # (8,32,4,4)
x_0, x_1 = x.chunk(2, dim=1) # (8,16,4,4)(8,16,4,4)
# channel attention
xn = self.avg_pool(x_0) #(8,16,1,1)
xn = self.cweight * xn + self.cbias #(8,16,1,1)
xn = x_0 * self.sigmoid(xn) #(8,16,4,4)
# spatial attention
xs = self.gn(x_1) # (8,16,4,4)
xs = self.sweight * xs + self.sbias # (8,16,4,4)
xs = x_1 * self.sigmoid(xs) # (8,16,4,4)
# concatenate along channel axis
out = torch.cat([xn, xs], dim=1) # (8,32,4,4)
out = out.reshape(b, -1, h, w) #(1,256,4,4)
out = self.channel_shuffle(out, 2)
return out
channel shuffle,1,2,3,4,5,6, 7, 8
2x4 = 1,2,3,4 / 5,6,7,8 = 1,2,3,4,5,6, 7, 8
4x2 = 1,5/ 2,6 / 3,7 / 4,8 = 1,5,2,6,3,7, 4, 8
参数量
W 1 W_1 W1, W 2 W_2 W2, b 1 b_1 b1, b 2 b_2 b2 一共 C 2 G × 4 = 2 C G \frac{C}{2G} \times 4 = \frac{2C}{G} 2GC×4=G2C
group normalization 的参数量和分的组数有关,每组 α \alpha α 和 β \beta β 两个参数, C 2 G × 2 = C G \frac{C}{2G} \times 2 = \frac{C}{G} 2GC×2=GC
总参数量为 3 C G \frac{3C}{G} G3C,还是小的比较夸张的
5 Experiments
5.1 Datasets and Metrics
- ImageNet for classification(top1 / top5)
- COCO for object detection and instance segmentation(mAP)
groups = 64
W 1 W_1 W1 和 W 2 W_2 W2 初始化为 0
b 1 b_1 b1 和 b 2 b_2 b2 初始化为 1
5.2 Classification on ImageNet-1k
5.3 Ablation Study

消融实验,group normalization 发挥了重要的作用
把 f c ( ⋅ ) f_c( \cdot) fc(⋅) 替换成 1x1 conv 没有替换前猛
5.4 Object Detection on MSCOCO
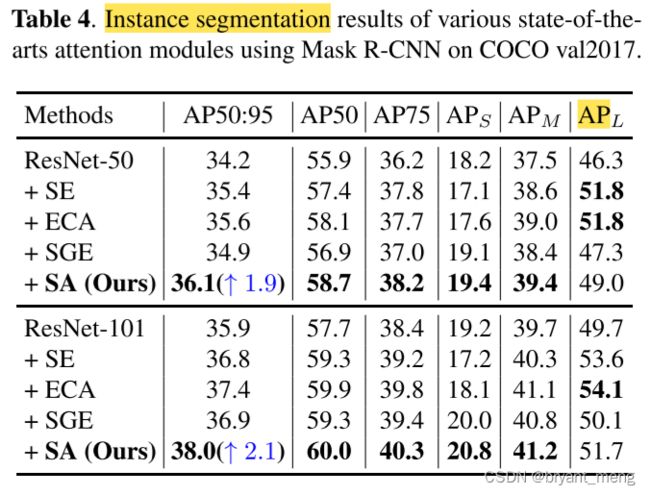
5.5 Instance Segmentation on MS COCO
大目标有提升,但不是最猛的
5.6 Visualization and Interpretation
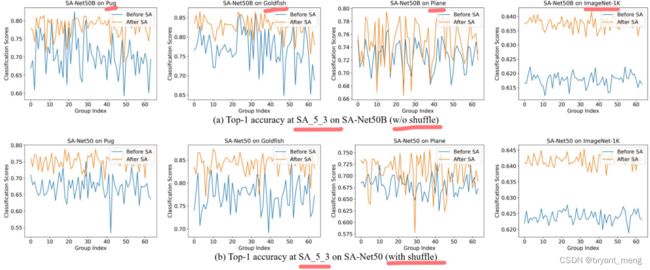
加了 SA 后(without shuffle 时),得分明显提高了,有 shuffle 操作以后得分会更高

SA_stageID_blockID
the importance of feature groups is likely to be shared by different classes in the early stages;
早期的 stage block 不同类别的同一组别中的特征相应重叠度比较高
后期特征多向性显现出来,SA_5_2 还是重叠比较多,可能是不怎么重要的层
6 Conclusion(own)
(1)SA 插在哪比较合适?
(2)Shuffle 的作用
(3)感兴趣的文章
- ECA-Net
- GCNet
- SGE