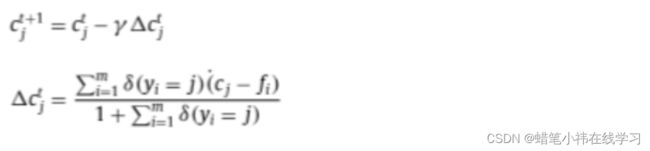阅读笔记-Minimum margin loss for deep face recognition

Minimum margin loss for deep face recognition

深度人脸识别的最小边缘损失

1、这篇论文要解决什么问题？要验证一个什么科学假设？

以往的损失函数不能解决类不平衡数据集存在的边际偏差问题，即所谓的长尾分布。MS-Celeb-1M和megface都存在长尾分布的问题，这意味着少数人拥有大部分的人脸图像，而大部分人拥有的人脸图像非常有限。使用具有长尾分布的数据集，训练好的模型容易过拟合样本丰富的类，从而削弱了长尾部分的泛化能力。具体来说，样本丰富的类往往在其类中心之间有相对较大的差距;相反，样本有限的类往往在其类中心之间有相对较小的差距，因为它们只占用空间中的一个小区域，因此很容易被压缩。这种边缘偏差问题是由于长尾类分布导致的，这导致了人脸识别的性能下降。

2、这篇论文有哪些相关研究，这些研究是怎么分类的？有哪些研究员值得关注？

边际损失考虑了一批样本中的所有样本对，迫使来自不同类别的样本对的边际大于阈值 θ，同时迫使来自同一类别的样本的边际小于阈值 θ。然而，强制类中两个距离最远的样本的距离小于不同类中两个距离最近的样本的距离过于严格，使得训练过程难以收敛。

Range Loss计算每个类内样本的距离，选择距离最大的两个样本对作为类内约束;同时，Range

Loss计算每一对类中心(又称中心对)的距离，并强制距离最小的中心对有一个大于指定阈值的裕度。但是，每次只考虑一个中心对是不全面的，可能会有更多的中心对的边缘值小于指定的阈值，因此由于学习速度慢，训练过程很难完全收敛。

AM-Softmax和ArcFace都采用了权重归一化和特征归一化，将所有特征都限制在一个超球体上。然而，强迫所有的特性都位于超球面，而不是更宽的空间是否过于严格?

3、论文中提到的解决方案是什么，关键点在哪儿？

论文提出了一种新的损失函数——最小边际损失(Minimum Margin Loss, MML)，旨在迫使所有类中心对的距离大于指定的最小边际损失。与Range Loss不同，MML惩罚所有“不合格”的类中心对，而不是只惩罚距离最小的中心对。MML重用由 centreLoss 不断更新的中心位置，并通过与Softmax Loss 和 centre Loss的联合监督指导训练过程。没有损失函数考虑设置类中心之间的最小边际。但是，需要有这样一个约束来纠正训练数据中由于类别不平衡而引起的边际偏差。

MML 指定了一个称为最小间隔的阈值。通过重用 centreLoss更新的类中心位置，MML根据指定的最小间隔过滤所有类中心对。对于那些距离小于阈值的对，相应的惩罚加到损失值

中。MML的详细描述如下:

式中，K为批次的类号，ci 和cj 分别为第 i和第 j个类中心，M为指定的最小间隔。在每个训练批次中，类中心由CentreLoss更新，使用以下两个方程:

其中γ是类中心的学习速率，t是迭代次数，δ(条件)是一个条件函数。满足条件时，δ(条件)= 1，否则 δ(条件)= 0。请注意，在Range Loss 中，一个类的中心是通过将该类的样本在一批中平均来计算的。但是，一个批次的大小是有限的，某一类的样品数量更是有限的。因此，以这种方式生成的类中心与真实的类中心相比并不精确。与 Range Loss 相比，MML的学习类中心更接近真实类中心。

4、论文中的实验是如何设计的？各个实验分别得到了什么结论？

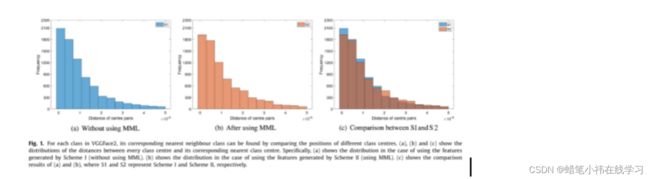
实验一：为了验证MML能真正扩大小于规定最小间隔的最近类中心对的距离，使用方案 I (Softmax Loss + Centre Loss)和方案II (Softmax Loss + Centre Loss + MML)训练的深度模型。方案一和方案二的区别在于方案二使用 MML作为监督的一部分，而方案一没有。利用提取的特征，计算每个类的中心位置，然后计算每个类中心与其最近邻类中心之间的距离。这些类中心的距离分布如图1所示。

这说明MML扩大了一些相邻中心对的距离，从而增加了有较大边缘的中心对的数量。

实验二：为验证MML能真正提高模型在人脸识别上的性能，在所有的实验中，都使用 VGGFace2作为训练数据，基于 initiation - resnet -v1，通过Tensorflow[根据5个方案实现和训练 5 个模型:SoftmaxLoss 、 Softmax Loss + Centre Loss 、 Softmax Loss + MarginalLoss、Softmax Loss + Range Loss 和 Softmax Loss + Centre Loss +MML。为方便起见，在实验结果中分别使用“ SoftmaxLoss”、“Centre Loss”、“Marginal Loss”、“Range Loss”和“MML”来表示这五种方案。在一个GPU (GTX 1080 Ti)上训练这5个模型，设置批处理大小为90，嵌入大小为512，权值衰减为5e−4，全连通层保持概率为 0.4。总迭代次数为275K，大约花费30小时。学习速率初始为 0.05，每100K次迭代除以10。除了Softmax Loss + Centre Loss + MML在训练开始前加载Softmax Loss + Centre Loss的训练模型作为预训练模型，因为这种方式使前者获得更好的识别性能。在测试期间，尽最大努力寻找能带来最高性能的参数设置。α和β分别设为5e−5和5e−8。MML的最小margin设置为280。每幅图像的深度特征是由全连接层的输出获得的，将原始测试图像的特征与水平翻转的对应图像的特征连接起来，因此每幅图像的最终特征尺寸为 2 *512，通过比较两个特征的欧氏距离和阈值，得到最后的验证结果。在 VGGFace2数据集上进行了两个实验，评估了这两个参数对总损耗的影响。

在第一个实验中，将β固定到5e−8，观察M对总损耗的影响如图2(a)所示。在第二个实验中，将M固定在280，并评估β与总损失的关系如图 2(b)所示。从图2(a)可以看出，设置M为0，即不使用MML，是不合适的，会导致总损耗较大。当M = 280时，总损耗最小。从图 2(b)可以看出，总损失在 β较大范围内保持稳定，但在β为5e−8时达到最小值。因此，在后续的实验中，将M和β分别固定为280和5e−8。

实验三：MegaFace 数据集作为干扰集，FaceScrub数据集作为测试集，使用官方提供的代码进行评估。将所提出的方法(MML)与不同的损耗以及MegaFace团队提供的一些基于深度学习的方法进行比较在人脸识别实验中，通过计算累积匹配特征(Cumulative Match Characteristics, CMC)曲线来衡量不同方法的排序能力，如图 3(a)所示。在人脸验证实验中，使用受试者工作特征(ROC)曲线来评估不同的方法。ROC曲线绘制了 1:1匹配器的错误接受率(FAR)与匹配器的错误拒绝率(FRR)，如图3(b)所示。表2列出了不同方法在1M干扰下识别率和验证率的数值结果。

实验四：在两个公共基准数据集LFW和YTF上评估所提出的方法

表3显示了本文方法和最新研究方法在 LFW和YTF数据集上的结果，可以看出:提出的MML优于Softmax Loss和Centre Loss，提高了LFW和YTF数据集上的验证性能。在LFW上，精度由 99.43%、99.50%提高到99.63%，在YTF上，精度由 94.9%、95.1%提高到 95.5%。此外，MML 在LFW和YTF数据集上都优于范围损耗和边际损耗。在 LFW上，精度由 99.50%、99.52%提高到99.63%，在YTF上，精度由95.1%、95.3%提高到95.5%。

实验五：为了验证MML的性能，SLLFW上进行了额外的实验。SLLFW使用与LFW相同的阳性对进行测试，但在 SLLFW中，通过人类众包从LFW中刻意挑选出3000对相似的面孔对来替代LFW中随机选取的阴性对。与LFW相比，SLLFW增加了更多的测试挑战，同样先进的方法的准确率下降了10-20%。

表4给出了SLLFW上不同方法的验证精度。表的上半部分显示了一些基准方法的结果。这些结果可以公开访问，并由SLLFW团队提供。从表4中可以看出，在 SLLFW上，MML比基准测试方法有更好的性能。与其他相关的损耗函数相比，MML 具有更高的精度。在表的上半部分，基准方法的准确率从LFW下降到SLLFW仅下降了16.75%到4.68%。相比之下，MML

算法的准确率下降了3.26%。在SLLFW上的实验结果进一步验证了所提方法的有效性。

实验六：按照1:1验证协议，将提出的MML与表5上半部分所示的最新方法进行比较。为了更公平的比较，直接将 MML与同一框架下其他流行的相关损失函数进行比较。结果表明，MML在IJB-B和IJB-C数据集上的表现优于表5上半部分所示的最新方法。此外，MML显示出比表5的下半部分中比较的相关损失函数更好的性能。