Matlab 最小二乘法 拟合平面 (PCL PCA拟合平面)
一、原理推导
最小二乘法 拟合平面是我们最常用的拟合平面的方法,但是有特殊的情况是用这种方法是不能拟合的,后续会加上这种拟合方法(RANSAC)。
matlab 最小二乘拟合平面(方法一) - 灰信网(软件开发博客聚合)
平面方程:Ax+By+Cz+D=0;
二、Matlab 实现
1、随机出来一些离散的点
>> clear
>> close all
>> % 随机生成一组(x,y,z)这些点的坐标离一个平面比较近
>> x0=1;L1=2;
>> y0=1;L2=2;
>> x=x0+rand(20,1)*L1;
>> y=y0+rand(20,1)*L2;
>> z=1+2*x+3*y;
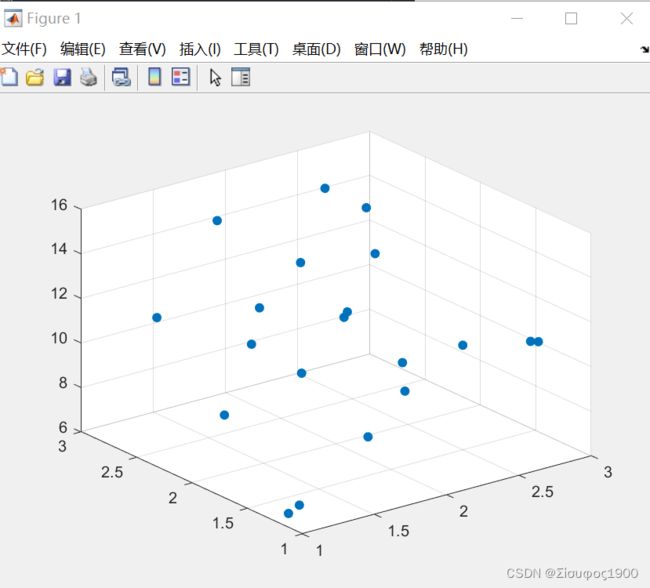
>> scatter3(x,y,z,'filled')2、将其写成矩阵的形式:
x_a=sum(x)/length(data);% length(data)==20
y_a=sum(y)/length(data);
z_a=sum(z)/length(data);
% 平方的均值====================================================
xx_a=sum(x.*x)/length(data);
yy_a=sum(y.*y)/length(data);
zz_a=sum(z.*z)/length(data);
xy_a=sum(x.*y)/length(data);
xz_a=sum(x.*z)/length(data);
yz_a=sum(y.*z)/length(data);3、求出a0 a1 a2也就是 -A/C -B/C -D/C
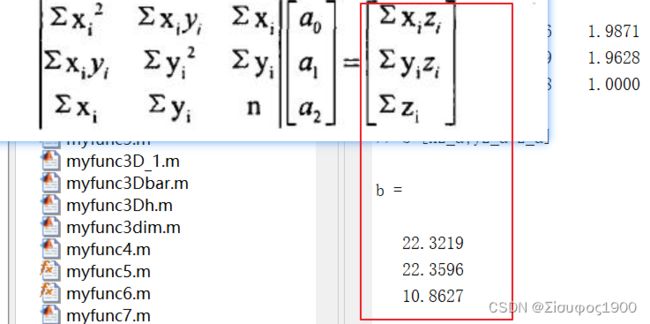
b=[xz_a;yz_a;z_a];
XYZ=A^-1 *b; % 方程求系数
a0=XYZ(1); % -A/C
a1=XYZ(2); % -B/C
a2=XYZ(3); % -D/C4、求平面法向量
V=[a0 a1 -1];% 平面法向量
nor=norm(V); % 向量的模
normalize_V=[a0/nor a2/nor -1/nor]; % 平面法向量归一化5、 开始绘制图像
scatter3(x,y,z,'filled')
hold on;
xfit=min(x):0.1:max(x); % 坐标系的坐标
yfit=min(y):0.1:max(y);
[XF,YF]=meshgrid(xfit,yfit);% 生产XY点列
ZF=a0*XF+a1*YF+a2; %计算Z的值
% 显示
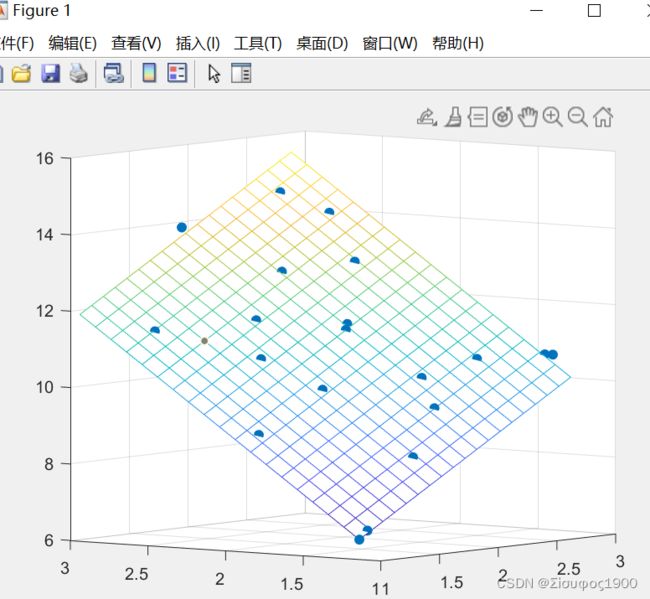
mesh(XF,YF,ZF)clear
close all
% 随机生成一组(x,y,z)这些点的坐标离一个平面比较近
x0=1;L1=2;
y0=1;L2=2;
x=x0+rand(20,1)*L1;
y=y0+rand(20,1)*L2;
z=1+2*x+3*y;
scatter3(x,y,z,'filled')
hold on;
data=[x,y,z];
x=data(:,1);
y=data(:,2);
z=data(:,3);
x_a=sum(x)/length(data);% length(data)==20
y_a=sum(y)/length(data);
z_a=sum(z)/length(data);
% 平方的均值====================================================
xx_a=sum(x.*x)/length(data);
yy_a=sum(y.*y)/length(data);
zz_a=sum(z.*z)/length(data);
xy_a=sum(x.*y)/length(data);
xz_a=sum(x.*z)/length(data);
yz_a=sum(y.*z)/length(data);
% 方程组的系数矩阵
A=[xx_a xy_a x_a;
xy_a yy_a y_a;
x_a y_a 1];
b=[xz_a;yz_a;z_a];
XYZ=A^-1 *b; % 方程求系数
a0=XYZ(1); % -A/C
a1=XYZ(2); % -B/C
a2=XYZ(3); % -D/C
V=[a0 a1 -1];% 平面法向量
nor=norm(V); % 向量的模
normalize_V=[a0/nor a2/nor -1/nor]; % 平面法向量归一化
% 开始绘制图像
scatter3(x,y,z,'filled')
hold on;
xfit=min(x):0.1:max(x); % 坐标系的坐标
yfit=min(y):0.1:max(y);
[XF,YF]=meshgrid(xfit,yfit);% 生产XY点列
ZF=a0*XF+a1*YF+a2; %计算Z的值
% 显示
mesh(XF,YF,ZF)
三维点集拟合:平面拟合、RANSAC、ICP算法_wishchin的博客-CSDN博客_三维曲面拟合算法
PCL 基于PCA的平面拟合
PCL的setIndices 函数
template void
pcl::PCLBase::setIndices (size_t row_start, size_t col_start, size_t nb_rows, size_t nb_cols)
{
if ((nb_rows > input_->height) || (row_start > input_->height))
{
PCL_ERROR ("[PCLBase::setIndices] cloud is only %d height", input_->height);
return;
}
if ((nb_cols > input_->width) || (col_start > input_->width))
{
PCL_ERROR ("[PCLBase::setIndices] cloud is only %d width", input_->width);
return;
}
size_t row_end = row_start + nb_rows;
if (row_end > input_->height)
{
PCL_ERROR ("[PCLBase::setIndices] %d is out of rows range %d", row_end, input_->height);
return;
}
size_t col_end = col_start + nb_cols;
if (col_end > input_->width)
{
PCL_ERROR ("[PCLBase::setIndices] %d is out of columns range %d", col_end, input_->width);
return;
}
indices_.reset (new std::vector);
indices_->reserve (nb_cols * nb_rows);
for(size_t i = row_start; i < row_end; i++)
for(size_t j = col_start; j < col_end; j++)
indices_->push_back (static_cast ((i * input_->width) + j));
fake_indices_ = false;
use_indices_ = true;
}
#if 1 // PCA的平面拟合
int main()
{
// Findnowd();
string path = "C:\\Users\\Albert\\Desktop\\pcd\\plane.pcd";
pcl::PointCloud::Ptr cloud(new pcl::PointCloud); // 创建点云(指针)
if (pcl::io::loadPCDFile(path, *cloud) == -1) //* 读入PCD格式的文件,如果文件不存在,返回-1
{
PCL_ERROR("Couldn't read file test_pcd.pcd \n"); //文件不存在时,返回错误,终止程序。
return 0;
}
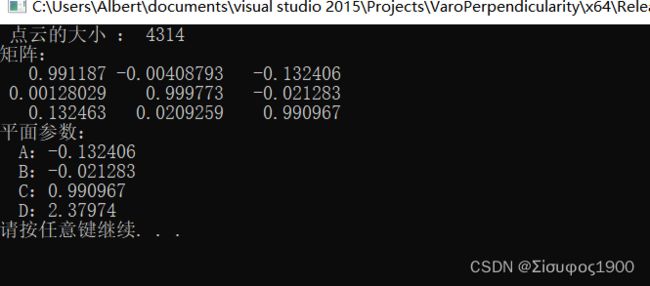
cout << " 点云的大小 : " << cloud->size() << endl;
pcl::PCA pca;
pca.setInputCloud(cloud);
Eigen::Matrix3f ve=pca.getEigenVectors();
cout << "矩阵:" << endl;
cout << ve << endl;
float A, B, C, D;
A = ve.col(2).row(0).value();
B = ve.col(2).row(1).value();
C = ve.col(2).row(2).value();
cout << "平面参数: " << endl;
cout << " A:" << A << endl;
cout << " B:" << B << endl;
cout << " C:" << C << endl;
//计算点云的质心
Eigen::Vector4d centroid;
pcl::compute3DCentroid(*cloud, centroid);
D = -(A * centroid[0] + B * centroid[1] + C * centroid[2]);
cout << " D:" << D << endl;
system("pause");
return (0);
}
#endif