【C语言\数据结构】图dijkstra最短路径 邻接矩阵(无项、有权)代码简单实现深度解析
这个代码是在图的邻接矩阵(无项、有权)的代码的基础上,添加了dijkstra最短路径函数,并且修改测试用例和主函数代码,图的邻接矩阵(无项、有权)的代码具体请查看 【C语言\数据结构】图之邻接矩阵(无向、有权)代码简单实现,这里就不过多赘述。
dijkstra最短路径实现思路
我们用一个案例来解释dijkstra最短路径的思路:
引入问题:求A顶点到达其他顶点的最短路径长度和最短路径。
引入定义:一个顶点到达其他顶点的直接距离的最小值就是最短路径。
例如,A顶点可以到达BDEF四个顶点,直接距离分别是AB2,AD4,AE3,AF5,这些距离的最短直接距离是AB2,则AB2就是最短路径。
因为如果你想从A到达其他顶点再从其他顶点到达B,第一步的距离一定要比AB这个直接距离大,所以AB就是最短路径。
接着我们引入judgment[i]和dist[i]和path[i]一维数组,分别表示A顶点到i顶点最短路径有无确定,A顶点到i顶点的最短路径,和该最短路径中i顶点的前一个顶点的下标。
首先我们访问A顶点,把A顶点到其他顶点的直接距离,修正到dist数组中,也就是目前A顶点到其他顶点的最短路径长度,path数组都存储A,因为目前的最短路径中,各顶点的前一个顶点的下标就是A。
接着我们找到最短的直接距离,依据定义我们知道AB就是A到B的最短路径,把judgment[B]修正为true,表示A到B的最短路径已经确定,然后访问B顶点,看看A到B再由B顶点到其他顶点的距离,会不会比目前存储的dist最短路径还要小,如果还要小,就修正dist和path数组。
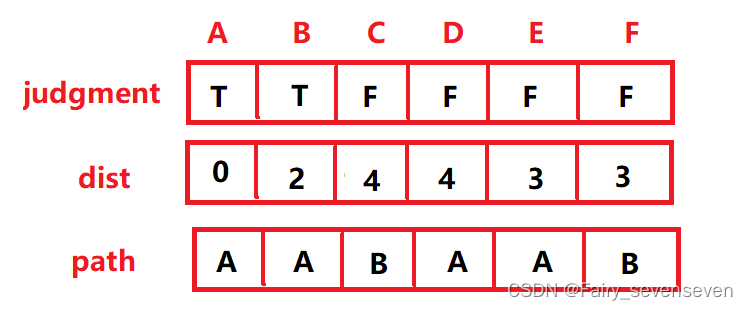
第一步,访问A顶点,得到:
第二步:找到dist中最小的值,这个值的judgement必须为false,已经确定的最短路径就不需要访问了。把judgement[B]置true,由B顶点修正dist和path。B顶点到C顶点距离是2,ABC距离一共是4,比dist存储的无穷要小,就修正dist,接着修正path。
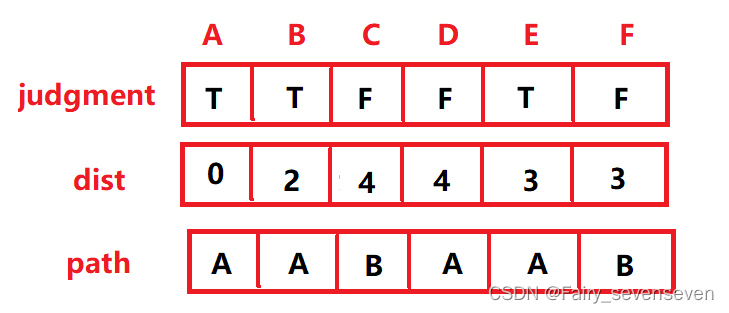
第三步:在还没有确定最短路径的顶点中,找dist最小的值,EF随便选一个,再由E顶点修正其他没有确定最短路径的顶点的dist和path,由于E只能到D或者A,A顶点最短路径已经确定不考虑,ED是2,2+3=5大于4,所以不用修正。
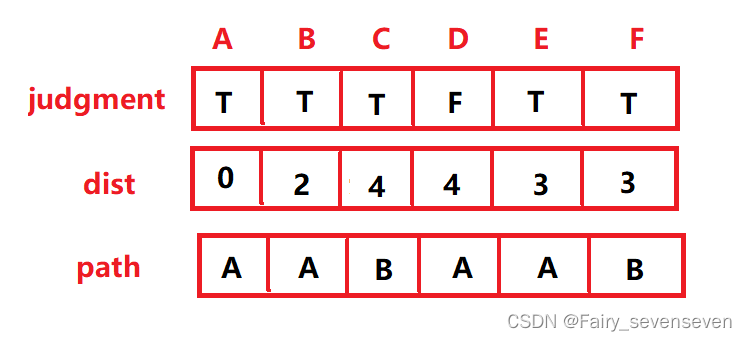
第四步:F中找到dist最小的顶点F,把F顶点的judgmen改为T,再通过F顶点修正dist和path,由于F只能到A或者B,AB的最短路径已经确定,不考虑。
第五步:在judgment为F的顶点中找到dist最小的顶点,CD选一个C,judgement改为T,由C顶点修正剩下judgment为F的顶点,C可以到BD,B最短路径已经确定不考虑,CD是2,C的dist4+2大于D的dist,不修正。
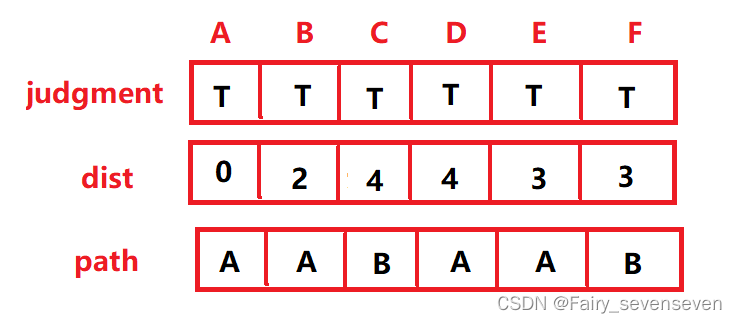
第六步:
编写dijkstra最短路径函数
void dijkstra(graph g, int v, int dist[], int path[]) {
bool judgment[MAX];
for (int i = 1; i <= g.vexnum; i++) {
judgment[i] = false;
dist[i] = g.arcs[v][i];
if (dist[i] < INFINITY || i == v) {
path[i] = v;
} else {
path[i] = -1;
}
}
dist[v] = 0;
judgment[v] = true;
for (int i = 1; i < g.vexnum; i++) {
int min = INFINITY;
int index_min;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] < min) {
index_min = j;
min = dist[j];
}
}
judgment[index_min] = true;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] > (dist[index_min] + g.arcs[index_min][j]) && (dist[index_min] + g.arcs[index_min][j]) < INFINITY) {
dist[j] = dist[index_min] + g.arcs[index_min][j];
path[j] = index_min;
}
}
}
}初始化操作
void dijkstra(graph g, int v, int dist[], int path[])
传入图g,以及v顶点下标,dist一维数组表示v顶点分别到其他顶点的最短路径长度,path一维数组表示v顶点分别到其他顶点的最短路径中终点的前一个顶点。
bool judgment[MAX]
创建一个判断数组,用来判断每一个顶点是否是最短路径,数据类型是bool型,如果已经确定顶点v到该顶点的最短路径,对应下标存储true,反之存储false。
bool judgment[MAX];
for (int i = 1; i <= g.vexnum; i++) {
judgment[i] = false;
dist[i] = g.arcs[v][i];
if (dist[i] < INFINITY || i == v) {
path[i] = v;
} else {
path[i] = -1;
}
}
初始化judgement,dist,path数组,首先对v顶点做处理,遍历每一个顶点,judgement初始值全部置false,dist数组数据全部更新为v顶点直接到其他各顶点的距离,如果v顶点到i顶点的边存在,或者v顶点自己到自己,则v顶点到i顶点的前一个顶点置为v,否则path置-1表示这条边不存在,这样就完成了对v顶点的访问,即初始化。
循环遍历维护dist和path
dist[v] = 0; judgment[v] = true;
先把v顶点到自己的最短路径值0,对应judgment值置true,表示已经确定v顶点到自己的最短路径。
for (int i = 1; i < g.vexnum; i++) {
int min = INFINITY;
int index_min;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] < min) {
index_min = j;
min = dist[j];
}
}
judgment[index_min] = true;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] > (dist[index_min] + g.arcs[index_min][j]) ) {
dist[j] = dist[index_min] + g.arcs[index_min][j];
path[j] = index_min;
}
}
}
最外层的循环仅表示以下内容需要循环g.vexnum-1次,也就是除去v顶点访问过的,其他顶点都需要访问一次。
int min = INFINITY;
int index_min;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] < min) {
index_min = j;
min = dist[j];
}
}judgment[index_min] = true;
找到v顶点到其他顶点j直接距离的最短距离,这个距离即是v顶点到j顶点的最短路径,因为如果你想从其他路径到j顶点,第一步走的路径一定要比v顶点直接到j顶点的距离长,所以这个最短的直接距离就是最短路径,找到v顶点到index_min顶点的最短路径,就访问该顶点,并且维护对应judgment的值,表示v顶点到index_min顶点的最短路径已经确定。
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] > (dist[index_min] + g.arcs[index_min][j]) ) {
dist[j] = dist[index_min] + g.arcs[index_min][j];
path[j] = index_min;
}
}
访问index_min顶点,根据这个顶点,看看能不能找到还没有确定的到达其他顶点的最短路径顶点的更小距离,维护dist和path数组。
如果这个j顶点的最短路径还没确定,并且v顶点到index_min顶点的最短路径,加上顶点index_min到j的路径长度比dist存储的v顶点到j顶点的最短路径还要小,就维护dist的值,并且把这个还没确定的最短路径的j的前一个顶点的下标维护到path数组。
依次循环,访问剩下的顶点,维护dist和path。
编写主函数
int main() {
graph g;
int start,end;
initGraph(g);
createGraph(g);
showGraph(g);
printf("\n输入起点和终点:\n");
scanf("%d%d",&start,&end);
int dist[MAX];//dist[i] v顶点到i定点最短路径的距离
int path[MAX];//path[i] v顶点到i定点最短路径中i的上一个顶点下标
dijkstra(g, start, dist, path);
printf("\n");
printf("dist:\n");
for(int i=1;i<=g.vexnum;i++){
printf("%d ",dist[i]);
}
printf("\n");
printf("path:\n");
for(int i=1;i<=g.vexnum;i++){
printf("%d ",path[i]);
}
printf("\n\n最短路径长度:\n%d\n",dist[end]);
char pathText[MAX]={""};
int cur=end;
pathText[strlen(pathText)]=end+'0';
while(cur!=start){
pathText[strlen(pathText)]=path[cur]+'0';
cur=path[cur];
}
printf("%d到%d的最短路径:\n",start,end);
for(int i=strlen(pathText)-1;i>=0;i--){
printf("%c ",pathText[i]);
}
printf("\n");
}
/*测试用例:
5 8
1 2 1
1 5 4
1 3 3
2 4 2
4 5 4
3 4 1
2 3 2
3 5 1
*/printf("\n\n最短路径长度:\n%d\n",dist[end]);
char pathText[MAX]={""};
int cur=end;
pathText[strlen(pathText)]=end+'0';
while(cur!=start){
pathText[strlen(pathText)]=path[cur]+'0';
cur=path[cur];
}
字符数组这样初始化,可以利用strlen函数计算自己的长度,以达到尾插的效果。
先把end终点顶点尾插进pathText
接着循环变量path数组,直到cur到start为止,这样最短路径的逆路程就存储在pathText数组中了。
printf("%d到%d的最短路径:\n",start,end);
for(int i=strlen(pathText)-1;i>=0;i--){
printf("%c ",pathText[i]);
}
printf("\n");
接下来只要从后往前遍历就可以正向输出最短路径了。
完整代码
#include
#include
#include
#include
#define MAX 100
#define INFINITY 9999
enum graphType {DG, UG, DN, UN}; //图的类型定义:有向图,无向图,有向网,无项网
typedef char vertexType;
typedef struct {
vertexType vexs[MAX];
int arcs[MAX][MAX];
int vexnum, arcnum;
graphType kind;
} graph;
void initGraph(graph &g) {
g.kind = UN;
printf("输入顶点数和边数:\n");
scanf("%d%d", &g.vexnum, &g.arcnum);
for (int i = 1; i <= g.vexnum; i++) {
g.vexs[i] = i;
}
for (int i = 1; i <= g.vexnum; i++) {
for (int j = 1; j <= g.vexnum; j++) {
if (i == j) g.arcs[i][j] = 0;
else g.arcs[i][j] = INFINITY;
}
}
}
void createGraph(graph &g) {
int start_index, end_index, weight;
printf("输入每条边的起点终点下标和边的权重:\n");
for (int i = 1; i <= g.arcnum; i++) {
scanf("%d%d%d", &start_index, &end_index, &weight);
g.arcs[start_index][end_index] = weight;
g.arcs[end_index][start_index] = weight;
}
}
void showGraph(graph &g) {
printf("邻接矩阵:\n");
for (int i = 1; i <= g.vexnum; i++) {
for (int j = 1; j <= g.vexnum; j++) {
printf("%d ", g.arcs[i][j]);
}
printf("\n");
}
}
void dijkstra(graph g, int v, int dist[], int path[]) {
bool judgment[MAX];
for (int i = 1; i <= g.vexnum; i++) {
judgment[i] = false;
dist[i] = g.arcs[v][i];
if (dist[i] < INFINITY || i == v) {
path[i] = v;
} else {
path[i] = -1;
}
}
dist[v] = 0;
judgment[v] = true;
for (int i = 1; i < g.vexnum; i++) {
int min = INFINITY;
int index_min;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] < min) {
index_min = j;
min = dist[j];
}
}
judgment[index_min] = true;
for (int j = 1; j <= g.vexnum; j++) {
if (judgment[j] == false && dist[j] > (dist[index_min] + g.arcs[index_min][j]) && (dist[index_min] + g.arcs[index_min][j]) < INFINITY) {
dist[j] = dist[index_min] + g.arcs[index_min][j];
path[j] = index_min;
}
}
}
}
int main() {
graph g;
int start,end;
initGraph(g);
createGraph(g);
showGraph(g);
printf("\n输入起点和终点:\n");
scanf("%d%d",&start,&end);
int dist[MAX];//dist[i] v顶点到i定点最短路径的距离
int path[MAX];//path[i] v顶点到i定点最短路径中i的上一个顶点下标
dijkstra(g, start, dist, path);
printf("\n");
printf("dist:\n");
for(int i=1;i<=g.vexnum;i++){
printf("%d ",dist[i]);
}
printf("\n");
printf("path:\n");
for(int i=1;i<=g.vexnum;i++){
printf("%d ",path[i]);
}
printf("\n\n最短路径长度:\n%d\n",dist[end]);
char pathText[MAX]={""};
int cur=end;
pathText[strlen(pathText)]=end+'0';
while(cur!=start){
pathText[strlen(pathText)]=path[cur]+'0';
cur=path[cur];
}
printf("%d到%d的最短路径:\n",start,end);
for(int i=strlen(pathText)-1;i>=0;i--){
printf("%c ",pathText[i]);
}
printf("\n");
}
/*测试用例:
5 8
1 2 1
1 5 4
1 3 3
2 4 2
4 5 4
3 4 1
2 3 2
3 5 1
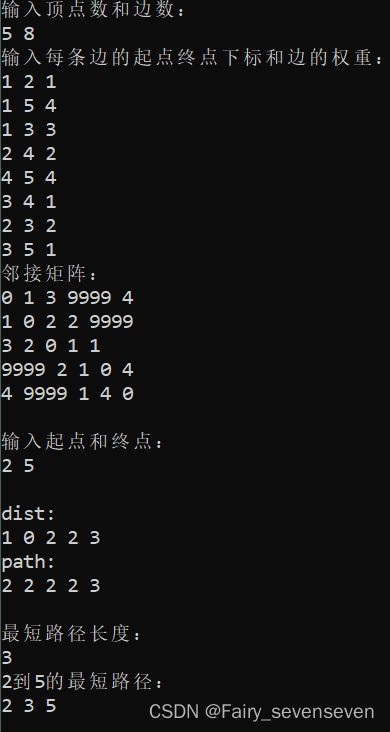
*/ 代码运行截图:
结尾
我们今天学习了dijkstra最短路径的实现,过程一共有三个一维数组judgement,dist和path,分别表示最短路径是否确定,最短路径长度,最短路径前一个顶点的下标。一个定义:一个顶点到达其他顶点的直接距离的最小值就是最短路径。依次访问dist最小值顶点,这个顶点的judgement需要为false,然后把这个fals改为true,接着由这个顶点修正其他false顶点的dist和path,依次循环。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!