LeetCode刷题--- 组合总和

个人主页：元清加油_【C++】,【C语言】,【数据结构与算法】-CSDN博客

个人专栏

力扣递归算法题

 http://t.csdnimg.cn/yUl2I   

【C++】         

 http://t.csdnimg.cn/6AbpV 

数据结构与算法

 http://t.csdnimg.cn/hKh2l

---

前言：这个专栏主要讲述递归递归、搜索与回溯算法，所以下面题目主要也是这些算法做的  

我讲述题目会把讲解部分分为3个部分：
1、题目解析

2、算法原理思路讲解

3、代码实现

---

组合总和

题目链接：组合总和

题目

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7]target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = 
​​[2,3,5]
target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2]target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

---

解法

题目解析

题目的意思非常简单给我们一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。

示例 ：

输入: candidates = [2,3,5]
target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

---

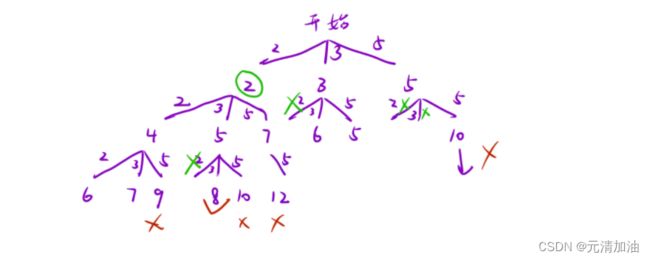
一、画出决策树

以 candidates = [2,3,5] 和 target = 8 为例子

决策树就是我们后面设计函数的思路

---

二、设计代码

（1）全局变量

    vector path;
    vector> ret;
    int aim;

• aim（target的值） 
• ret（存储符合target 值的组合）
• path（组合的路径记录）

（2）设计递归函数

void dfs(vector& candidates, int pos, int sum);

• 参数：nums（数组），pos（当前要处理的元素下标），sum（当前的组合相加的和）；
• 返回值：无；
• 函数作⽤：找出所有组合使得元素和为⽬标值；

递归流程：

1. 递归结束条件：判断 sum 的是否大于 aim ，若 sum 大于 aim 则返回，若 sum 等于 aim 则 将 path 的值放入 ret 后返回
2. 在每个递归状态中，枚举所有下标 i ，i 等于 pos
   1. ​​​​​​​将candidates[i] 添加⾄ path 数组末尾；
   2. sum 的值加上将candidates[i]；
   3. 对第 i 个位置进⾏递归；
   4. 回溯 sum 的值减去将candidates[i] ，再删除 path 数组末尾的元素；

以上思路讲解完毕，大家可以自己做一下了

---

代码实现

• 空间复杂度：O(target)。除答案数组外，空间复杂度取决于递归的栈深度，在最差情况下需要递归 O(target) 层。

class Solution 
{
public:
    vector path;
    vector> ret;
    int aim;


    void dfs(vector& candidates, int pos, int sum)
    {
        if (sum > aim )
        {
            return;
        }

        if (sum == aim)
        {
            ret.push_back(path);
            return;
        }

        

        for (int i = pos; i < candidates.size(); i++)
        {
            path.push_back(candidates[i]);
            sum += candidates[i];
            dfs(candidates, i, sum);
            sum -= candidates[i];
            path.pop_back();
        }
    }

    vector> combinationSum(vector& candidates, int target)
    {
        aim = target;
        sort(candidates.begin(), candidates.end());

        dfs(candidates, 0, 0);

        return ret;
    }
};