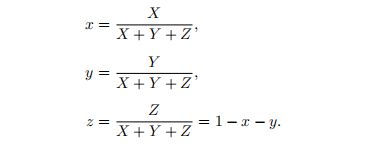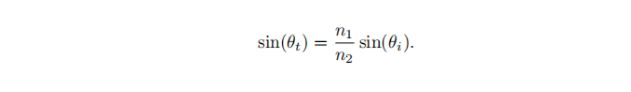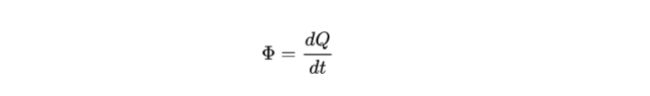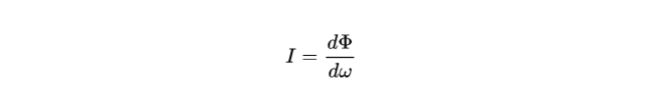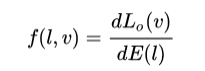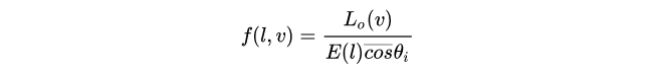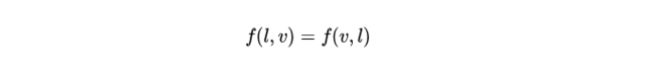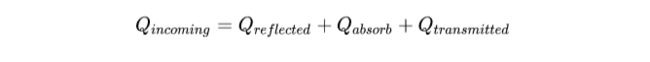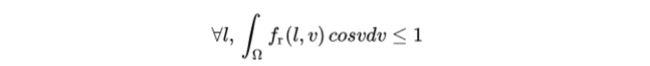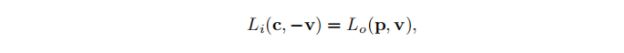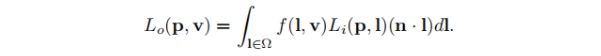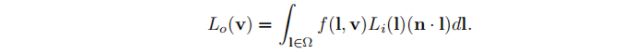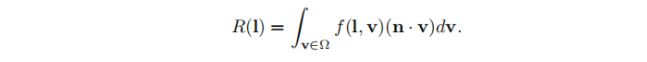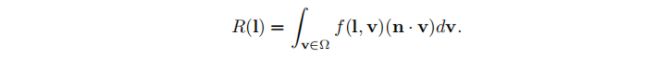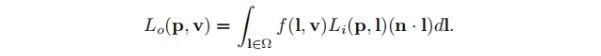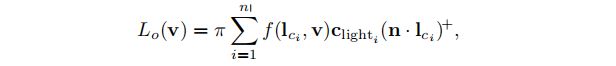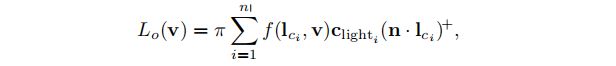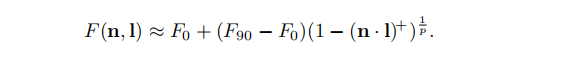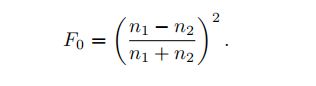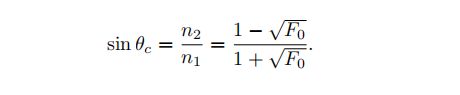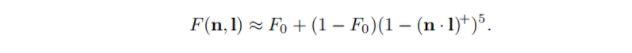光照学研究
光与颜色
光学是一个古老的物理学课题,因为光的存在,才使我们能够看到五彩缤纷的世界,颜色是人类对光的主观感受。
几何光学
几何光学从宏观上研究光传播所服从的定律。几何光学吧光抽象成一条条射线,用几何作图法描述各种光学现象。并有以下定律:
光的直线传播定律
光的独立传播定律
光的反射定律和折射定律
Light Quantities(光量)
如何基于物理的渲染的第一步就越是有精确的方式来量化光线。这里有几个名词,Radiometry 辐射度学,他会涉及光的物理传输的核心领域。Photometry(光度学),他处理的是人眼对光波的灵敏度。 人类对颜色的感知是一种心理物理现象(pasychophysical phenomenon)。
辐射度学 (Radiometry)
Radiometry deals with the measurement of electromagnetic radiation.(辐射学是研究电磁辐射的测量),这种辐射是以波的形式传播。不同波长的电磁波具有相同相位的两个相邻点之间的距离,例如两个相邻的波峰具有不同的性质。在自然界中,电磁波的波长范围很广,从长度不到百分之一纳米的伽玛波到长度到达数万公里的极低频(ELF)电波。人类所能看到的光波只是这一范围的一小部分,从大约400纳米的紫外光扩展到700多纳米的红光。
辐射度量(radiometry quantities)
用于测量电磁辐射的各个方面:总能量(overall energy)、功率(随时间变化的能量,energy over time)和相对于面积、方向或两者的功率密度(power density)。
光谱功率(spectral power distribution)SPD
为了准确描述光是如何表示和采样以计算图像的,我们必须首先建立辐射测量学的一些背景——研究电磁辐射在环境中的传播。渲染中特别感兴趣的是大约 380 nm 和 780 nm 之间的电磁辐射波长,它解释了人类可见的光。the lower wavelenght ( λ ≈ 400 nm)are the bluish colors, the middle wavelengths ( λ ≈ 550 nm) are the greens, and the upper wavelengths ( λ ≈ 650 nm)are the reds.
在本章中,我们将介绍描述电磁辐射的四个关键量:通量、强度、辐照度和辐射度。这些辐射量分别由它们的光谱功率分布(SPD) 描述 - 一种波长分布函数,描述了每个波长的光量。
在辐射度学中基本单位是辐射通量(radiant flux),Φ。辐射通量是随时间-功率流动的辐射能量,以瓦特(watt,W)为单位量。
辐照度(irradiance)是辐射通量相对于面积的密度,即dΦ/ dA。辐照度是根据面积来定义的,面积可以是空间中想象的面积,但通常是物体的表面。它的单位是瓦特每平方米。
spectral representation(频谱表示)
【扩展部分】立体角(Solid Angle)他是角度概念的三维扩展,一个角度可以被认为是一个平面的连续方向集合的大小度量,他的弧度Value等于这个方向的集合与半径为1的封闭圆相交的弧的长度。 类似地,立体角可以表示三维空间中连续的方向集合的大小,测量单位为球面度(steradians,缩写为sr),其定义为和半径为1的封闭球体相交斑块的面积。 立体角是由符号ω表示。
辐射强度(radiant intensity,I)是辐射通量对方向,更准确地说是立体角(dΦ/ dω)的密度。它的单位是瓦特每球面度。
辐射率(radiance,L)是单一射线中电磁辐射的量度。 更准确地说,它被定义为辐射通量对单位面积和单位立体角的密度:
环境中的辐射可以看作是5个变量的函数(或6个,包括波长),称为辐射分布(radiance distribution)。 其中三个变量指定位置,另外两个指定方向。这个函数描述了所有的光在空间中移动。 渲染过程可以理解为,眼睛和屏幕定义一个点和一组方向(例如,通过每个像素的射线),然后在眼睛处对每个方向进行计算。
在着色方程中,辐射率通常用 Lo(x,d) 或 Li(x,d)表示, 这意味着从x点发出的光或者进入x点的光。 方向向量d表示射线的方向,根据惯例,它总是指向远离x的方向。 然而这种惯例在Li的情况下会有些令人困惑, 因为d指向光传播的相反方向,因为对于点积之类的计算这很方便。
辐射率的一个重要特性是它不受距离的影响, 忽视大气影响,如雾。 换句话说,不管与观察者的距离有多远,一个表面都会有相同的亮度。 距离越远,表面覆盖的像素越少,但每个像素处的表面辐射是恒定的。
所有的辐射量都有光谱分布,因为这些分布是在波长的密度上为基础的,它们的单位是原始量除以纳米。(例如辐照度)。
这个面积是在垂直于射线的平面上测量的, 如果测量的其他方向的表面上的辐射率,那么必须要使用余弦校正因子。 可能会遇到术语“投影面积”来定义辐射率的情况。
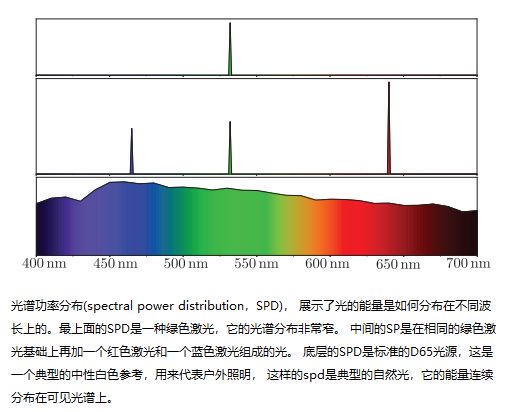
大多数光波是包含有许多不同波的混合物。最直观的是光谱功率分布(spectral power distribution,SPD), 展示了光的能量是如何分布在不同波长上的。
光度学(photometry)
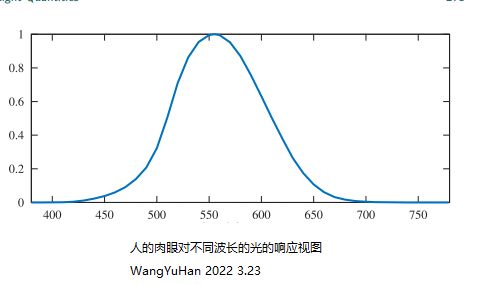
光度学,与辐射度学一样,只是它通过人眼的灵敏度来衡量一切。通过将CIE光度曲线(CIE photometric curve)1与以555nm为中心的钟型曲线相乘,可以将辐射度计算的结果转换为光度单位。
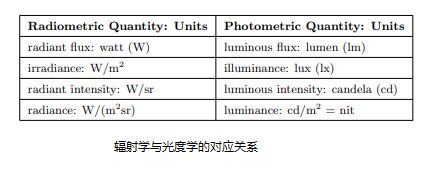
转换曲线和测量单位是光度学理论和放射线学理论的唯一区别。每一个辐射量都有一个等效的度量光度量。
色度学(Colorimetry)
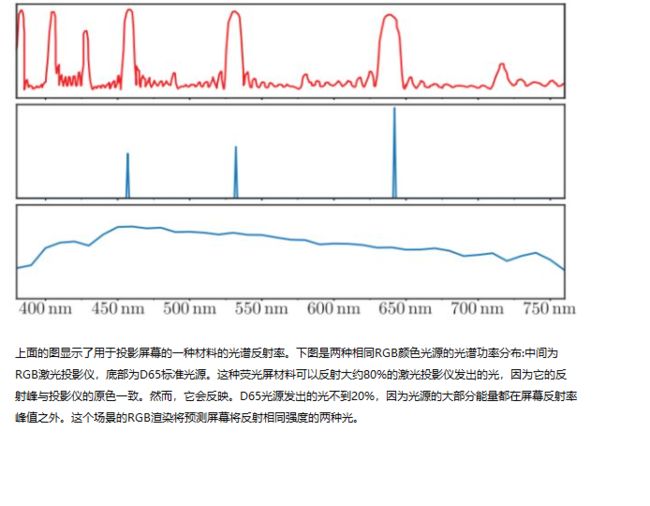
我们已经看到,我们对光的颜色的感知与光的SPD(光谱功率分布)密切相关。 我们也看到这不是简单的一对一对应。 上面SPD图的底部的SPD和中间SPD完全不同,但被认为是完全相同的颜色。 色度学研究的是光谱功率分布和人眼对颜色的感知之间的关系。
人类可以分辨大约1000万种不同的颜色。 人眼对于颜色感知,是通过视网膜上三种不同类型的锥受体工作的,每种类型的受体对不同的波长有不同的反应。 其他动物有不同数量的颜色受体,在某些情况下多达15个。 因此,对于一个给定的SPD,我们的大脑只从这些受体接收到三种不同的信号。这也是为什么只用三个数字就可以精确地表示任何颜色刺激。
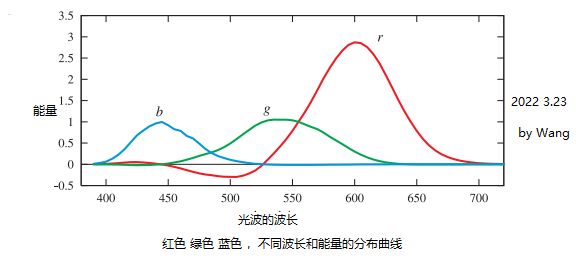
CIE (Commission Internationale d 'Eclairage)提出了一套测量颜色的标准条件,并使用它们进行了颜色匹配实验。 调色时,三种不同颜色的光投射在白色屏幕上,使它们的颜色叠加在一起形成一个色块。 下图中展示了一组三种光(r、g和b)的测试结果。 这些光几乎是单色的,每一束光的能量分布都集中在一种波长附近:r为645 nm, g为526 nm, b为444 nm。 将每组匹配权值与测试波长相关联的函数称为颜色匹配函数(color-matching functions)。
这些颜色匹配函数将光谱功率分布转换为三个值。 对于任意的光谱分布,颜色匹配函数可以乘以每个结果曲线下的分布和面积(即,积分)给出相对的数值,设置光的颜色,以匹配由光谱感知到的颜色。 考虑到不同的光谱分布可以分解为相同的三个权值, 在观察者看来它们是一样的。 给出匹配权值的光谱分布称为条件等色(metamers)。
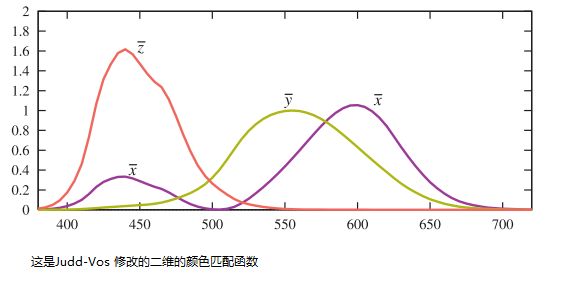
三种加权的r,g和b光源不能直接表示所有可见颜色,因为它们的颜色匹配功能对于各种波长具有负权重。 CIE提出了三种具有颜色匹配功能的假想光源,这些光源对所有可见波长都为正。 这些曲线是原始的r,g和b颜色匹配函数的线性组合。 这要求它们在某些波长处的光源光谱功率分布为负,因此这些光是无法实现的数学抽象。 它们的色彩匹配函数分别表示为x(λ),y(λ)和z(λ),如下图所示。色彩匹配函数y(λ)与测光曲线相同
,因为辐射率通过该曲线转换为亮度。
与前一组颜色匹配函数一样,x(λ)、y(λ)和z(λ)通过乘法和积分将任何SPDs(λ)减为三个数字:
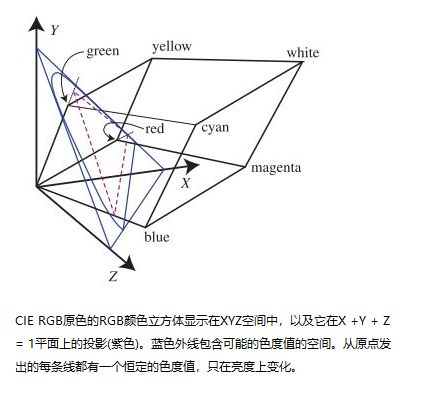
这些X,Y和Z三刺激值(tristimulus values)是在CIE XYZ空间中定义颜色的权重。将颜色分为亮度(luminance)( (brightness) )和色度(chromaticity)通常很方便。色度是颜色的特性,与亮度无关。 例如,尽管亮度不同,但两种蓝色,一种暗和一种亮可以具有相同的色度。
为此,CIE通过将颜色投射到X + Y + Z = 1平面上来定义二维色度空间。 见下图。
此空间中的坐标称为x和y,其计算如下:
z值不提供任何其他信息,因此通常将其省略。色度坐标( chromaticity coordinates)x和y值的图被称为CIE1931色度图(CIE 1931 chromaticity diagram)。具体看下图。图中的弯曲轮廓显示了可见光谱的颜色所在的位置,连接光谱两端的直线称为紫线。 黑点表示光源D65的色度,它是经常使用的白点-用于定义白色或消色差(无色)刺激的色度。
渲染中有几个有意思的RGB空间,每个由R,G和B原色和一个白点定义。为了比较它们,我们将使用另一种类型的色度图,称为CIE 1976 UCS(均匀色度标度)图。该图是CIELUV色彩空间的一部分,CIE(以及另一个色彩空间,CIELAB)采用了CIELUV色彩空间,目的是为XYZ空间提供在感知上更统一的替代方案。在CIE XYZ空间中,可以感觉到相同数量的颜色对的距离差异最多可以达到20倍。CIELUV对此进行了改进,使该比率最多降低了四倍。这种增加的感知均匀性使得1976年的图表比1931年的图表要好得多,以比较RGB空间的色域。对感知均匀色彩空间的持续研究最近导致了ICTCP和Jzazbz空间。 这些色彩空间在视觉上比CIELUV更均匀,尤其是对于现代显示器典型的高亮度和饱和色而言。 但是,基于这些色彩空间的色度图尚未得到广泛采用,因此我们在本章中使用CIE 1976 UCS图,例如在下图的情况下。
在上图中所示的三个RGB空间中,sRGB是迄今为止在实时渲染中最常用的空间。尽管当前sRGB颜色空间在实时渲染中无处不在,但可能会增加使用更宽的颜色空间。最直接的好处是针对广色域显示器的应用程序,但即使对于针对sRGB或Rec 709显示器的应用程序也有优势。 当在不同的色彩空间中执行常规的渲染操作(例如乘法)时,结果会有所不同,并且有证据表明,在DCI-P3或ACEScg空间中执行这些操作所产生的结果要比在线性sRGB空间中执行这些结果更为准确。
从RGB空间到XYZ空间的转换是线性的,可以使用从RGB空间的基色和白点派生的矩阵来完成。通过矩阵求逆和串联,可以导出矩阵以将XYZ转换为任何RGB空间,或在两个不同的RGB空间之间转换。 注意,在这种转换之后,RGB值可以为负或大于1。 这些是超出色域的颜色,即在目标RGB空间中无法再现。 可以使用各种方法将这些颜色映射到目标RGB色域。
一种常用的转换是将RGB颜色转换为灰度亮度值。 由于亮度与Y系数相同,因此此操作仅是RGB到XYZ转换的“ Y部分”。 换句话说,它是RGB系数与RGB到XYZ矩阵的中间行之间的点积。 对于sRGB和Rec 709空间,等式为
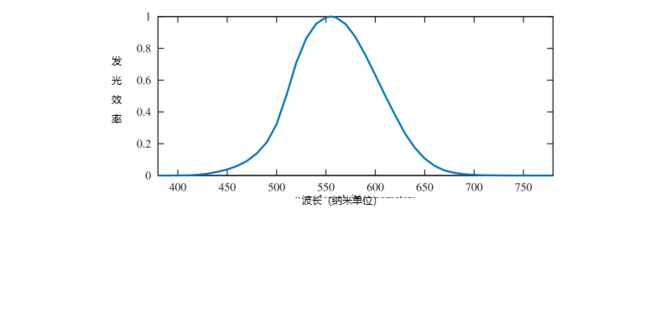
这再次将我们带到了光度曲线,如下图所示。将该曲线表示标准观察者的眼睛对各种波长的光的响应方式,再乘以三个基色的光谱功率分布,然后对每个结果曲线进行积分。 所得的三个权重就是上面的亮度方程式。 灰度强度值不相等的部分是红色,绿色和蓝色,是因为眼睛对各种波长的光具有不同的灵敏度。
比色法可以告诉我们两种颜色刺激是否匹配,但无法预测它们的出现。 给定的XYZ颜色刺激的外观在很大程度上取决于照明,周围颜色和先前条件等因素。 颜色外观模型(CAM)(例如CIECAM02)试图解决这些问题并预测最终的颜色外观。
使用RGB渲染(Rendering with RGB Colors)
严格来说,RGB值表示感知量而不是物理量。 从技术上讲,使用它们进行物理渲染是类别错误。正确的方法是对频谱量执行所有渲染计算,并通过密集采样或在适当的基础上进行投影来表示,并仅在最后转换为RGB颜色。
例如,最常见的渲染操作之一是计算从物体反射的光。物体表面通常会更多的反射一些波长的光相对于其他的波长,如其光谱反射率(spectral reflectance)曲线所描述。计算反射光颜色的严格正确方法是将入射光的SPD乘以每个波长处的光谱反射率,得出反射光的SPD,然后将其转换为RGB颜色。取而代之的是,在RGB渲染器中,将灯光和曲面的RGB颜色相乘在一起,以提供反射光的RGB颜色。在一般情况下,这不会给出正确的结果。 为了说明,我们将看一个极端的例子,如下图所示。
色调映射(Tone Mapping)
上面一直在讨论显示的编码 将线性辐射度值转换为显示硬件的非线性的编码之过程。通过显示编码应用的函数是显示器的电光传递函数(EOF)的逆函数,可确保输入的线性值与显示器发出的线性辐射度值想匹配。
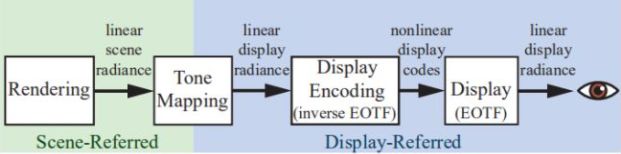
色调映射(Tone mapping)或色调再现(tone reproduction )是将场景辐射值转换为显示辐射值的过程。在此步骤中应用的变换称为“端到端传递函数(end-to-end transfer function)”或“场景到屏幕的变换(scene-to-screen transform)”。 图像状态的概念是理解色调映射的关键。有两种基本的图像状态。 参考场景(Scene-referred)的图像是参照场景辐射值定义的,而显示参考(display-referred)的图像是参照显示辐射值定义的。图像状态与编码无关。 处于任一状态的图像都可以线性或非线性编码。下图显示了图像状态,色调映射和显示编码如何在成像管线(imaging pipeline)中组合在一起,该成像管线处理从初始渲染到最终显示的颜色值。
了解色调映射的目标,最好将其视为图像复制的一个实例。 图像再现的目标是创建一个显示参考图像,该图像将在给定显示属性和观看条件的情况下尽可能接近地再现观众在观察原始场景时所获得的感知印象。 见下图。
有一种图像复制的目标稍有不同。首选图像重现(Preferred image reproduction)旨在创建在某种意义上看起来比原始场景更好的显示参考图像。
考虑到典型场景中的亮度范围超出显示能力几个数量级,再现与原始场景相似的感知印象的目标具有挑战性。 场景中至少某些颜色的饱和度(纯度)也可能远远超过显示能力。尽管如此,摄影,电视和电影确实可以像原始文艺复兴时期的画家一样,产生令人信服的原始场景感性肖像。 通过利用人类视觉系统的某些特性,可以实现这一目标。
视觉系统补偿绝对亮度的差异,这种能力称为适应(adaptation)。由于这种能力,尽管昏暗的房间的屏幕上显示的室外场景的再现亮度小于原始场景的1%,但它仍可以产生与原始场景相似的感觉。然而,通过适应提供的补偿是不完善的。 在较低的亮度水平下,感知的对比度降低(史蒂文斯效应(Stevens effect)),感知的“色彩感”(亨特效应(Hunt effect))也降低。
其他因素会影响再现+的实际或感知对比度。 显示器的周围(显示器矩形外部的亮度水平,例如房间照明的亮度)可能会增加或减少可察觉的对比度(巴特尔森-布勒曼效应(Bartleson-Breneman effect))。显示器眩光(Display flare)是通过显示器缺陷或屏幕反射而添加到显示图像中的多余光,通常会在很大程度上降低图像的实际对比度。这些效果意味着,如果我们想保持与原始场景类似的感知效果,则必须提高显示参考图像值的对比度和饱和度。
然而,对比度的增加加剧了现有问题。 由于场景的动态范围通常比显示器的动态范围大得多,因此我们必须选择要再现的亮度值的狭窄窗口,该窗口上方和下方的值将被裁剪为黑色或白色。 增强对比度会进一步缩小此窗口。 为了部分抵消暗值和亮值的裁剪,可以使用柔和的滚降来带回一些阴影和高光细节。
所有这些都导致了S型(S形)色调再现曲线,类似于光化学膜所提供的曲线。这绝非偶然。 柯达和其他公司的研究人员对光化学膜乳剂的性能进行了仔细的调整,以产生有效且令人愉悦的图像。 由于这些原因,形容词“filmic”常常出现在色调映射的讨论中。
曝光(exposure)的概念对于色调映射至关重要。在摄影中,曝光是指控制落在胶片或传感器上的光量。 然而,在渲染中,曝光是在应用色调再现变换之前对场景参考图像执行的线性缩放操作。曝光的棘手方面是确定要应用的缩放比例。 色调的转换和曝光紧密地联系在一起。通常在设计色调转换时会期望将其应用于已以某种方式曝光的场景参考图像。
通过曝光进行缩放然后应用色调重现变换的过程是一种全局色调映射,其中将相同的映射应用于所有像素。 相反,基于周围像素和其他因素,局部色调映射过程使用不同的像素到像素映射。实时应用程序几乎只使用了全局色调映射(有一些例外),因此我们将重点介绍这种类型,首先讨论色调再现转换,然后再讨论曝光。
重要的是要记住,场景参考图像和显示参考图像本质上是不同的。物理操作仅在对场景引用的数据执行时才有效。 由于显示限制和我们已经讨论过的各种感知效果,在两个图像状态之间始终需要进行非线性变换。
基于物理的光照(Physics of Light)
光与物质的相互作用形成基于物理的着色的基础。
在物理光学中光背建模为电磁横波(transverse wave),一种垂直于其创博方向振荡电场和磁场的波。这两个场的振荡是耦合的。 磁场和电场矢量相互垂直,并且它们的长度之比是固定的。该比率等于相速度。下图
线性偏振(linearly polarized)
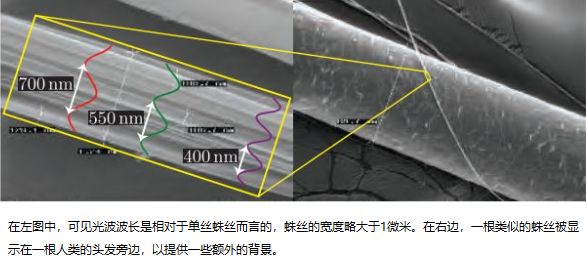
对于可见光,单个波长的大小在大约400-700纳米的范围内。 为了给这种长度一些直觉,它大约是蜘蛛丝单线宽度的一半到三分之一,而蜘蛛丝本身不到人类头发宽度的50之1。
光波携带能量。能量流的密度等于电场和磁场强度的乘积,因为强度彼此成正比,因此与电场的平方强度成正比。我们专注于电场,因为电场对物质的影响远大于磁场。在渲染中,我们关注随时间变化的平均能量流,它与平方波幅度成正比。该平均能量流密度是辐射度(irradiance),用字母E表示。
光波线性组合。 总波是分量波的总和。但是,由于辐射度与振幅的平方成正比,因此这似乎会导致自相矛盾。例如,将两个相等的波相加会不会导致辐射度出现“ 1 + 1 = 4”的情况?而且由于辐射度衡量能量流,这会不会违反能量守恒? 这两个问题的答案分别是“有时”和“否”。
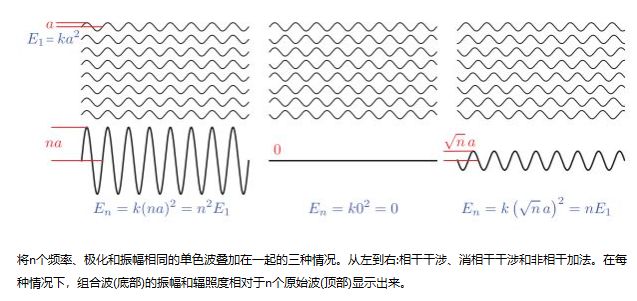
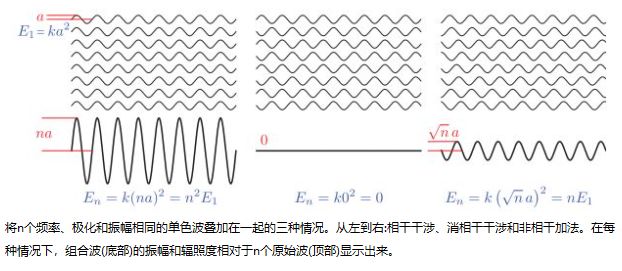
为了说明,我们将看一个简单的情况:添加n个单色波,除了相位以外,其他均相同。n个波中每个波的振幅为a。 如前所述,每个波的辐射度E1与a^2成正比,换句话说,对于某些常数k,E1 = ka^2。
下图显示了这种情况的三个示例方案。在左侧,所有波浪都以相同的相位排列并互相增强。 组合波辐射度是单个波辐射度的n^2倍,比单个波辐照射值的总和大n倍。这种情况称为相长干涉(constructive interference)。 在图的中心,每对波处于相反相位,彼此抵消。 组合波具有零振幅和零辐照度。 这种情况是相消干涉(destructive interference)。
相长干涉和相消干涉是相干叠加的两种特殊情况,其中波的波谷和波谷以某种一致的方式排列。根据相对相位关系,n个相同波的相干叠加会导致其辐射度是单个波的0到n2倍之间的任意值。
但是,大多数情况下,将波加在一起时,它们是彼此不相干的,这意味着它们的相位是相对随机的。上图右边对这种情况进行了说明。在这种情况下,组合波的振幅为√n a,并且单个波的辐射度线性增加到一个波辐射度的n倍,正如人们所期望的那样。
相长干涉和破坏性干涉似乎违反了能量守恒。但是,上图并未显示全部内容,而是仅在一个位置显示了波的相互作用。随着波在空间中传播,波之间的相位关系从一个位置改变到另一个位置,如下图所示。在某些位置,波产生相长干涉,并且组合波的辐照度大于各个波的辐照值之和。 在其他位置,它们具有相消干涉,导致组合的辐照度小于各个波辐照度值的总和。这不会违反能量守恒定律,因为通过相长干涉获得的能量和通过相消干涉损失的能量始终会相互抵消。
当物体中的电荷振荡时会发出光波。引起振荡的部分能量(热,电能,化学能)被转换为光能,该光能从物体上散发出去。 在渲染中,此类对象被视为光源。
发出光波后,它们穿过空间,直到遇到与之相互作用的一些物质。 大多数光物质相互作用的核心现象很简单,并且与上面讨论的发射情况非常相似。振荡电场推和拉物质中的电荷,使它们依次振荡。振荡的电荷发出新的光波,该光波将入射光波的某些能量重定向到新的方向。 这种反应称为散射,是各种光学现象的基础。
散射光波具有与原始波相同的频率。 通常情况下,当原始波包含多个频率的光时,每个波分别与物质相互作用。在一种频率下入射的光能不会对在另一种频率下发出的光能有所贡献,除了特殊情况(相对罕见)的情况(例如荧光和磷光)
一个孤立的分子向各个方向散射光,在强度上有一定的方向变化。更多的光分散在接近原始传播轴的方向上,无论是向前还是向后。分子作为散射体的效率(附近光波完全被散射的机会)随波长而变化很大。 短波长的光比长波长的光更有效的散射。
在渲染中,我们关注许多分子的集合。光与这些聚集体的相互作用不一定类似于与孤立分子的相互作用。从附近分子散射的波通常是相互相干的,因此会产生干扰,因为它们源自同一入射波。 本节的其余部分专门讨论从多个分子散射光的几种重要特殊情况。
微分子(Particles)
在理想的气体下(ideal gas),分子不会互相影响,因此它们的相对位置是完全随机且不相关的。尽管这是一个抽象概念,但它对于正常大气压下的空气来说是一个相当不错的模型。在这种情况下,从不同分子散射的波之间的相位差是随机的并且不断变化。 结果,散射波是不相干的,其能量呈线性增加,如下图的右侧所示。 换句话说,从n个分子散射的聚集光能是从单个分子散射的光的n倍。
相反,如果分子紧密堆积成比光波长小得多的簇,则每个簇中的散射光波是同相的,并且会相长干涉。如上图左边所示,这导致散射波能量平方相加。因此,从n个小分子簇中散射的光强度是从单个分子中散射的光的n^2倍,这是相同数量的分子在理想气体中散射的光的n倍。这种关系意味着对于每立方米固定密度的分子,将分子聚集成簇将显着增加散射光的强度。使团簇更大,同时仍保持整体分子密度恒定,将进一步增加散射光强度,直到团簇直径变得接近光波长。 超过该点,簇大小的额外增加将不会进一步增加散射光强度。
这个过程解释了为什么云和雾如此强烈地散射光。 它们都是由冷凝产生的,冷凝是空气中水分子聚集成越来越大的簇的过程。 即使水分子的总密度不变,这也会大大增加光散射。
介质(Media)
另一个重要的情况是光通过均质介质(homogeneous medium)传播,该介质是一个均匀分布的相同分子的体积。 分子间距不必像晶体一样完全规则。 如果液体和非晶态固体的成分是纯净的(所有分子都相同)并且没有间隙或气泡,则它们在光学上可以是均质的。
在均匀的介质中,散射波排列成一条直线,从而它们在除原始传播方向之外的所有方向上都具有相消干涉。将原始波与从单个分子散射的所有波合并后,最终结果与原始波相同,除了其相速度和(在某些情况下)振幅。最终波没有任何散射-它已被相消干涉有效地抑制了。
原始波和新波的相速度之比定义了介质的光学特性,称为折射指数(index of refraction)(IOR)或折射率(refractive index),用字母n表示。一些媒体具有吸收性(absorptive)。 它们将部分光能转换成热量,从而导致波的振幅随距离呈指数下降。下降率由衰减指数(attenuation index)定义,用希腊字母κ(kappa)表示。n和κ通常都随波长而变化。 这两个数字加在一起,完全定义了介质如何影响给定波长的光,并且它们经常合并为一个复数n +iκ,称为复数折射率(complex index of refraction)。折射率将光相互作用的分子水平细节抽象化,使介质可以视为连续体积,这要简单得多。
虽然光的相速度不会直接影响外观,但速度的变化会影响外观,我们将在后面解释。 另一方面,光的吸收会直接影响视觉效果,因为它会降低光的强度,并且(如果随波长而变化)也会改变其颜色。 下图显示了一些光吸收的示例。
非均质介质通常可以建模为具有嵌入式散射粒子的均质介质。抑制均匀介质中散射的相消干涉是由于分子的均匀排列以及分子产生的散射波的均匀排列引起的。分子分布的任何局部变化都会打破这种破坏性相消干涉模式,允许散射光波传播。这种局部变化可以是不同分子类型,气隙,气泡或密度变化的簇。无论如何,它都会像前面讨论的粒子一样散射光,其散射特性也取决于簇的大小。 甚至气体都可以用这种方式建模。对于这些,“散射粒子”是由分子的恒定运动引起的瞬态密度波动。 该模型可以为气体建立有意义的n值,这对于理解其光学性质很有用。 下图显示了光散射的一些示例。
散射和吸收均取决于比例。 在小场景中不产生任何明显散射的介质在较大场景下下可能具有相当明显的散射。例如,当观察室内的一杯水时,看不到空气中的光散射和水中的吸收。 但是,在扩展环境中,两种效果都可能很明显,如下图所示。
在一般情况下,介质的外观是由散射和吸收的某种组合造成的,如下所示。
散射程度决定了浑浊,高散射产生不透明的外观。 除少数罕见的例外(例如,下图中的乳白色玻璃)外,固体和液体介质中的颗粒往往大于光波长,并且会平均散射所有可见波长的光。因此,任何色彩通常是由吸收的波长依赖性引起的。 介质的亮度是这两种现象的结果,特别是白色是高散射和低吸收性相结合的结果。
物体表面(Surface)
从光学角度看,物体表面是一个二维界面,用于分隔具有不同折射率值的体积。在典型的渲染情况下,外部体积包含空气,其折射率约为1.003,为简单起见通常假定为1。 内部体积的折射率取决于制造对象的物质。
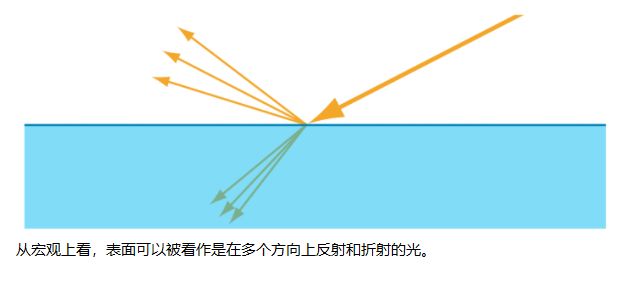
当光波撞击表面时,该表面的两个方面都会对结果产生重要影响:两侧的物质以及表面的几何形状。当光波撞击表面时,该表面的两个方面都会对结果产生重要影响:两侧的物质以及表面的几何形状。我们将从关注物质方面开始,假设最简单的可能的表面几何形状,即完美的平面。我们将“外部”(入射波或入射波起源的那一侧)的折射率表示为n1,将“内部”(波将在穿过表面后传输的那一侧)的折射率表示为 n2。
我们在上一节中已经看到,光波在遇到材料成分或密度(即折射率)的不连续性时会发生散射。分离不同折射率的平面是一种特殊的不连续类型,它以特定的方式散射光。 边界条件要求平行于表面的电场分量是连续的。换句话说,电场矢量到表面平面的投影必须在表面的任一侧匹配。 这有几个影响:
1.在表面上,任何散射波必须与入射波同相或异相180°。因此,在表面处,散射波的峰值必须与入射波的峰值或波谷对齐。这限制了散射波只能沿着两个可能的方向传播,一个继续向前进入表面,而一个则向后退。 其中第一个是透射波(transmitted wave),第二个是反射波(reflected wave)。
2.散射波必须具有与入射波相同的频率。 我们在这里假设一个单色波,但我们讨论的原理可以应用于任何一般波,首先将其分解为单色分量。
3.当光波从一种介质移动到另一种介质时,相速度(波在介质中传播的速度)与相对折射率(n1 / n2)成比例地变化。 由于频率是固定的,因此波长也按比例变化为(n1 / n2)。
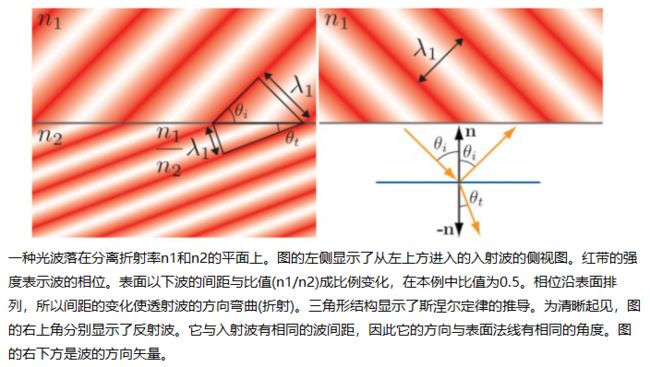
最终结果如下图所示。
反射和入射波方向与表面法线的夹角为θi。 透射波方向以角度θt弯曲(折射(refracted)),与角度θi具有以下关系:
这个折射方程称为斯涅尔定律(Snell’s law)。 它用于全局折射效果。
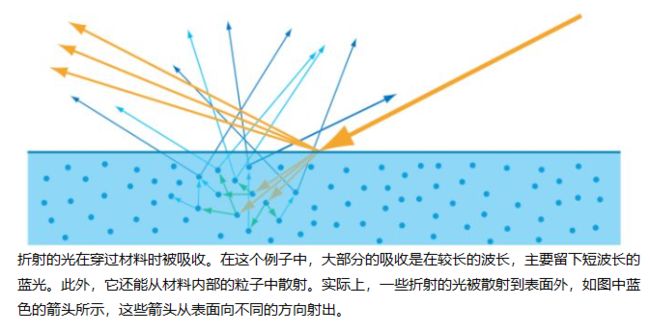
尽管折射通常与透明材料(例如玻璃和晶体)有关,但折射也发生在不透明物体的表面。当不透明物体发生折射时,光线会在物体内部发生散射和吸收。 光线与物体的介质相互作用,就像下图中的各种液体一样。就金属而言,内部包含许多自由电子(未与分子结合的电子),这些电子“吸收”折射光能并将其重定向到反射波中。 这就是金属具有高吸收率和高反射率的原因。
我们已经讨论过的表面折射现象-反射和折射-要求折射率的突然变化,发生在小于单个波长的距离上。 折射率的逐渐变化不会使光分裂,而是会导致光路弯曲,类似于折射中发生的不连续弯曲。当空气密度因温度变化(例如海市蜃楼和热变形)而变化时,通常可以看到这种效果。如下图所示。
如果将物体浸入具有相同折射率的物质中,则即使具有明确边界的物体也不会具有可见表面。 在没有折射率变化的情况下,不会发生反射和折射。如下图所示。
到目前为止,我们一直专注于物质在表面任一侧的影响。现在,我们将讨论影响表面外观的另一个重要因素:几何形状。 严格来说,不可能有一个完全平坦的平面。每个表面都有某种不规则性,即使仅构成该表面的单个原子也是如此。然而,远小于波长的表面不规则对光没有影响,远大于波长的表面不规则有效地使表面倾斜而不影响其局部平坦度。只有大小在1–100波长范围内的不规则结构,才会通过称为衍射(diffraction)的现象使表面的行为不同于平坦的平面。
在渲染中,我们通常使用几何光学(geometrical optics),而忽略诸如干涉和衍射之类的波效应。这等效于假设所有表面不规则性都小于或小于光波长。 在几何光学中,光被建模为射线而不是波。在光线与表面相交的点上,该表面在局部被视为平面。可以将下图右下角的图视为反射和折射的几何光学图,与该图其他部分中呈现的波图相反。从这一点开始,我们将一直关注几何光学领域。
比波长大得多的表面凹凸会改变表面的局部方向。 当这些不规则尺寸太小而无法单独渲染(换句话说,小于一个像素)时,我们将其称为微几何(microgeometry)。 反射和折射的方向取决于表面法线。 微观几何的作用是改变表面上不同点的法线,从而改变反射和折射的光的方向。
即使表面上的每个特定点仅在单个方向上反射光,每个像素仍覆盖许多在各个方向上反射光的表面点。外观由所有不同反射方向的合计结果驱动。下图显示了两个表面的示例,这些表面在宏观尺度上具有相似的形状,但微观几何形状却显着不同。
为了进行渲染,而不是显式地对微几何模型建模,我们将其进行统计处理并将其视为具有随机分布的微结构法线。结果,我们将表面建模为在连续方向上反射(和折射)光。 这种宽度的扩展以及反射和折射细节的模糊性取决于微几何法线向量的统计方差,即表面微尺度粗糙度(roughness)。如下图所示。
折射光继续与物体的内部体积相互作用。 如前所述,金属反射大多数入射光并迅速吸收其余的光。相反,非金属表现出各种各样的散射和吸收行为,具有低散射和吸收的材料是透明的,任何折射的光都可以穿过整个物体。如下图所示:
这种次表面散射(subsurface-scattered)光以距入射点不同的距离离开表面。 出入口距离的分布取决于材料中散射粒子的密度和性质。 这些距离与着色比例(像素大小或着色样本之间的距离)之间的关系很重要。如果出入距离与着色比例相比较小,则出于着色目的,可以假定它们实际上为零。 这允许将次表面散射与表面反射结合到一个局部着色模型中,在一个点上发出的光只取决于同一点上的入射光。但是,由于次表面散射光的外观与表面反射光的外观明显不同,因此将它们分成单独的着色项非常方便。 高光(specular)项模拟表面反射,而漫反射(diffuse)项模拟局部次表面散射(local subsurface scattering)。
如果出入口距离与着色比例相比较大,则需要专门的渲染技术来捕获在某一点进入曲面并从另一点出射的光的视觉效果。 局部和全局次表面散射之间的差异如下图所示。
重要的是要注意,局部和全局次表面散射技术可以对完全相同的物理现象进行建模。每种情况的最佳选择不仅取决于材料的属性,而且取决于观察范围。例如,当渲染一个孩子在玩塑料玩具的场景时,可能需要采用全局技术来准确渲染孩子的皮肤,并且局部漫射着色模型足以满足该玩具的需要。这是因为皮肤中的散射距离比塑料中的散射距离大得多。 但是,如果相机距离足够远,则皮肤散射距离将小于像素,并且局部着色模型对于儿童和玩具都将是准确的。相反,在极端特写镜头中,塑料将表现出明显的非局部次表面散射,并且需要全局技术来准确地渲染玩具。
视觉感知(Visual Perception)
视觉科学(Vision Science)
视觉是人最强的感觉。视觉产生信息远远超过听觉,嗅觉和味觉。这是因为光的物理特性直接导致的结果
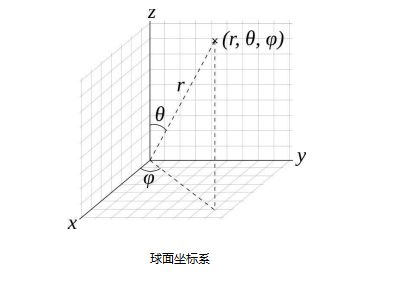
球面坐标 (Spherical Coordinate)
前面已经讲解过立体角 所以在这里求立体角w用微分的形式来表达:
辐射通量/光通量 (Radiant Flux)
辐射通量及冠通量描述单位时间内穿过截面的光能,每单位时间的辐射能量 ,用Φ表示,单位是W,瓦特
其中Q表示辐射能(Radiant energy),单位是J,焦耳。
辐射强度/发光强度 (Radiant Intensity)
对一个点光源,辐射强度表示单位(立体角)的辐射能量,用符号 I表示。单位 W • sr^-1:
就是单位立体角的辐射通量。单位 W • sr^-1,瓦特每球面度。
辐射率/光亮度 (Radiance)
辐射率(Radiance,又译作光亮度,用符号 L 表示),表示物体表面沿某一方向的明亮程度,它等于每单位投影面积和单位立体角上的辐射通量,单位是 ,瓦特每球面度每平方米。在光学中,光源的辐射率,是描述非点光源时光源单位面积强度的物理量,定义为在指定方向上的单位立体角和垂直此方向的单位面积上的辐射通量。光亮度 L 也可以理解为发光程度 I 在表面 dA 上的积分。
一种直观的辐射率的理解方法是:将辐射率理解为物体表面的微面元所接收的来自于某方向光源的单位面积的光通量,因此截面选用垂直于该方向的截面,其面积按阴影面积技术计算。
辐射率的微分形式:
其中:Φ是辐射通量,单位瓦特(W);w是立体角,单位球面度(sr)。另外需要注意的是,辐射率使用物体表面沿目标方向上的投影面积,而不是面积。概括一下:辐射率(Radiance,又译作光亮度),表示每单位立体角每单位投影面积的辐射通量,通常用符号 L 表示,单位是W • sr^-1 • m^-2,瓦特每球面度每平方米。
辐照度/辉度 (Irradiance)
辐照度用符号E表示,指入射表面的辐射通量,即单位时间内到达单位面积的辐射通量,辐射通量是对于面积的密度,单位W/^2瓦特每平方米。
辐照度可以写成辐射率(Radiance),在入射光所形成的半球的积分:
其中,Ω是入射光所形成的半球。L(ω)是沿ω方向的光亮度。
双向反射分布函数 BRDF(Bidirectional Reflectance Distribution Function)
双向反射分布函数 是描述真实感图形学中最核心的概念之一,它描述物体表面将光能从任何一个入射方向反射到任何一个试点方向的反射特性,即入射光线经过莫个表面反射后如何在各个出射方向上的分布。
BRDF是绝大多数的图形学算法的基本模型。BRDF定义的是出射辐射率的微分和入射辐照度的微分之比:
要理解这个方程的含义,可以想象一个表面被一个来自围绕着角度 l 的微立体角的入射光照亮,而这个光照效果由表面的辉度 dE 来决定。
表面会反射此入射光到很多不同的方向,在给定的任意出射方向 v,光亮度 dLo 与辐照度 dE成一个比例。而两者之间的这个取决于 l 和 v 的比例,就是 BRDF。
BRDF的非微分形式(Bidirectional Reflectance Distribution Function)
BRDF的着色方程(Bidirectional Reflectance Distribution Function)
其中 k 是每个光源的索引。使用⊗符号(分段向量乘法),是因为 BRDF 和辉度(irradiance)都是 RGB 向量。考虑到入射和出射方向都拥有两个自由度(通常参数化是使用两个角度:相对于表面法线的仰角θ和关于法线的旋转角度φ),一般情况下,BRDF 是拥有四个标量变量的函数。
另外,各向同性 BRDFs(Isotropic BRDFs)是一个重要的特殊情况。这样的 BRDF 在输入和输入方向围绕表面法线变化(保持相同的相对夹角)时保持不变。所以,各向同性 BRDF 是关于三个标量的函数。
BRDF的可逆性
BRDF 的可逆性源自于亥姆霍兹光路可逆性(Helmholtz Recoprpcity Rule)。
BRDF 的可逆性即,交换入射光与反射光,并不会改变 BRDF 的值:
BRDF的线性特征
很多时候,材质往往需要多重 BRDF 计算以实现其反射特性。表面上某一点的全部反射辐射度可以简单地表示为各 BRDF 反射辐射度之和。例如,镜面漫反射即可通过多重 BRDF 计算加以实现。
BRDF的能量守恒性质
BRDF必须遵循能量守恒性质及入射光的能量与出射光的总能量相等:
此外还有2个性质:
基于物理的BRDF(Physics of BRDF)
基于物理的渲染归结为计算沿着某组视线进入相机的辐射。引入辐射学入射辐射的表示法,对于给定的视线,我们需要计算的量为Li(c,-v),其中c是摄像机位置, -v是沿视线的方向。我们使用-v是由于两种约定。首先,Li()中的方向矢量始终指向给定点,在这种情况下,它就是摄像机的位置。其次,视图向量v始终指向相机。
在渲染中,场景通常被建模为对象之间的介质集合,通常所描述的介质是适量的相对清洁的空气,不会影响射线的辐射度,因此可以忽略不计。有时,射线可能通过一种介质传播,这种介质确实通过吸收或散射对其辐射有明显的影响。此类介质称为参与介质( participating media),因为它们参与了灯光在场景中的传输,在现在只假设不存在参与介质,因此进入摄像机的辐射等于在摄像机方向上离开最近的物体表面的辐射:
其中p是视线与最近的物体表面的交点。我们不考虑透明度和全局次表面散射的情况。换句话说,我们专注于局部反射现象,该现象将使当前着色点反射的光线重定向回外部。这些现象包括表面反射以及局部次表面散射,并且仅取决于入射光方向l和出射视图方向v。局部反射率由双向反射率分布函数(bidirectional reflectance distribution function)(BRDF)量化,表示为f(l,v)。
在其原始推导中,将BRDF定义为均匀表面。 也就是说,假设BRDF在整个表面上相同。 但是,现实世界(以及渲染场景)中的对象很少在其表面上具有统一的材质属性。即使是由单一材料组成的物体,例如由银制成的雕像,也将具有划痕,失去光泽的斑点,污点和其他变化,导致其视觉特性从一个表面点改变到另一个表面点。从技术上讲,根据空间位置捕获BRDF变化的功能称为空间变化(spatially varying )BRDF(SVBRDF)或空间(spatial)BRDF(SBRDF)。然而,这种情况在实践中非常普遍,因此经常使用较短的BRDF,并隐式地假定它取决于表面位置。
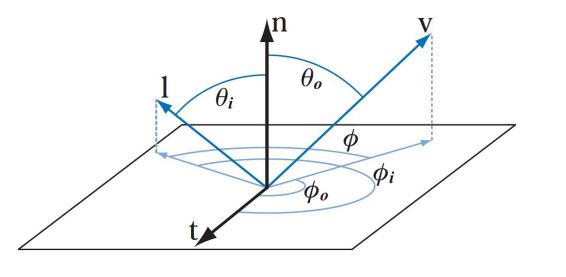
传入和传出方向分别具有两个自由度。 一个常用的参数化涉及两个角度:相对于表面法线n的仰角θ和关于n的方位角(水平旋转)φ。在一般情况下,BRDF是四个标量变量的函数。各向同性【指物理化学方面不会因为方向不同而导致性质不一样】(Isotropic)BRDF是重要的特殊情况。当传入和传出方向围绕曲面法线旋转时,此类BRDF保持相同,并且它们之间的相对角度保持相同。下图显示了两种情况下使用的变量。各向同性BRDF是三个标量变量的函数,因为仅需要光源和相机旋转之间的单个角度φ即可。这意味着,如果将均匀的各向同性材料放在转盘上并旋转,则在给定固定光源和摄像头的情况下,对于所有旋转角度,该材料都将显示相同的效果。
由于我们忽略了诸如荧光和磷光之类的现象,因此我们可以假定给定波长的入射光以相同波长反射。反射的光量可以根据波长而变化,可以通过两种方式之一对其进行建模。要么将波长视为BRDF的附加输入变量,要么将BRDF视为返回光谱分布值。尽管有时在脱机渲染中使用第一种方法,但在实时渲染中始终使用第二种方法。 由于实时渲染器将光谱分布表示为RGB三元组,这仅仅意味着BRDF返回一个RGB值。
为了计算Lo(p,v),我们将BRDF合并到反射率方程(reflectance equation)中:
积分符号上的l∈Ω下标表示对位于表面上方单位半球(以表面法线n为中心)的l个向量进行积分。请注意,l连续扫过入射方向的半球-它不是特定的“光源方向”。这个想法是,任何进入的方向都可以(并且通常会)具有与之关联的辐射度。 我们用dl表示围绕l的微分立体角。总之,反射率方程式表示出射辐射率等于入射辐射率的积分(over l in Ω)乘以BRDF乘以n与l之间的点积。
为了简洁起见,在本章的其余部分中,我们将省略Li(),Lo()和反射率方程式中的表面点p:
在计算反射率方程时,通常使用球坐标φ和θ对半球进行参数化。对于此参数化,微分立体角dl等于sinθi dθi dφi。使用该参数化,可以得出方程式下图的双积分形式,该形式使用球坐标(回想一下(n·l)= cosθi):
θi、φi、θo和φo的角度如上面的弟3个图所示。
在某些情况下,使用稍微不同的参数设置较为方便,将仰角µi = cosθi和µo = cosθo的余弦作为变量,而不是角度θi和θo本身。对于该参数化,微分立体角dl等于dµi dφi。 使用(µ,φ)参数化可产生以下整数形式:
仅在光线方向和视图方向都在表面上方的情况下才定义BRDF。可以通过将BRDF乘以零或不首先评估此类方向的BRDF来避免光线方向在表面下方的情况。但是,表面下的视线方向又如何,换句话说,点积n·v为负?从理论上讲,这种情况永远都不会发生。 该表面将背对摄像机,因此是不可见的。 然而,插值顶点法线和法线映射在实时应用中都很常见,在实践中可以创建这样的情况。通过将n·v clamp 为0或使用其绝对值可以避免针对表面下的视图方向评估BRDF,但是两种方法都可能导致瑕疵。Frostbite引擎使用n·v的绝对值加上一个较小的数字(0.00001)来避免被零除。另一种可能的方法是“软clamp”,当n和v之间的角度超过90°时,该clamp逐渐变为零
在实践中,用于渲染的BRDF经常违 Helmholtz reciprocity而没有明显的瑕疵,除了特别需要互易性的脱机渲染算法(例如双向路径跟踪)外。 但是,在确定BRDF在物理上是否合理时,它是有用的工具。
第二个约束是能量守恒-输出能量不能大于输入能量(不算发光的发光表面,在特殊情况下要处理)。脱机渲染算法(例如路径跟踪)需要节能以确保收敛。对于实时渲染,不需要精确的节能,但是近似节能很重要。用BRDF渲染的表面严重违反了节能原则,该表面会太亮,因此看起来不现实。
定向半球反射率(directional-hemispherical reflectance)R(l)是与BRDF有关的函数。它可以用来衡量BRDF的节能程度。 尽管其名称有些令人生畏,但定向半球反射率是一个简单的概念。它测量从给定方向反射的光量,该光被反射到表面法线周围半球的任何出射方向。 本质上,它可以测量给定方向的能量损失。 该函数的输入是输入方向矢量l,其定义如下:
请注意,这里的v像反射率方程中的l一样,被扫描到整个半球,并不代表单一的观察方向。
一个类似但在某种意义上相反的函数,可以类似地定义半球方向反射率(hemispherical-directional reflectance)R(v):
如果BRDF是互易的,则半球方向反射率和方向半球反射率相等,并且可以使用相同的函数来计算任一个。 在两个反射率可互换使用的情况下,定向反射率(Directional albedo)可以用作两个反射率的总称。
由于能量守恒,定向半球反射率R(l)的值必须始终在[0,1]范围内。 反射率值为0表示所有入射光被吸收或丢失的情况。如果所有的光都被反射,则反射率将为1。在大多数情况下,反射率将介于这两个值之间。像BRDF一样,R(l)的值随波长而变化,因此出于渲染目的将其表示为RGB矢量。由于每个成分(红色,绿色和蓝色)都限制在[0,1]范围内,因此可以将R(l)的值视为简单的颜色。 请注意,此限制不适用于BRDF的值。作为分布函数,如果BRDF描述的分布高度不均匀,则在某些方向(例如高光的中心)可以具有任意高的值。 BRDF保持能量的要求是,对于l的所有可能值,R(l)不大于1。
最简单的BRDF是Lambertian,Lambertian BRDF具有恒定值。区分Lambertian 着色的众所周知的(n·l)因子不是BRDF的一部分,而是下图公式的一部分。
尽管它很简单,但是Lambertian BRDF经常用于实时渲染以表示局部次表面散射。Lambertian表面的方向性半球反射率也是一个常数。 对于f(l,v)的恒定值评估方程式
,得出与BRDF有关的定向半球反射率的以下值:
Lambertian BRDF的恒定反射率值通常称为漫反射颜色(diffuse color)Cdiff或 反照率( albedo) ρ。在本文中,为了强调与次表面散射的联系,我们将这个量称为次表面反照率ρss。 上面公式的BRDF给出以下结果:
1 /π因子是由以下事实造成的:在半球上积分余弦因子会产生π值。BRDF中经常出现此类因子。
光照( Illumination)
反射率方程式(下图)中的Li(l)(入射辐射)项表示从场景其他部分入射到表面点的光。全局照明(Global illumination )算法通过模拟光线在整个场景中的传播和反射方式来计算Li(l)。这些算法使用渲染方程(rendering equation),其中反射方程是一个特例。我们将重点介绍局部照明(local illumination),它使用反射率方程来计算每个表面点的局部着色。在局部照明算法中,给出了Li(l),不需要计算。
在现实场景中,Li(l)包括来自各个方向的非零辐射,无论是直接从光源发出还是从其他表面反射。与定向光与精准光不同,真实世界的光源是覆盖非零立体角的区域光。在本文中,我们使用Li(l)的限制形式,仅由品定向光与精准光组成。
尽管精准光源和定向光是非物理的抽象,但它们可以作为物理光源的近似值导出。这样的推导很重要,因为它使我们能够将这些灯光合并到基于物理的渲染框架中,并确信我们了解所涉及的错误。
我们采用一个小的远距离区域光,并将lc定义为指向其中心的向量。我们还将光线的颜色Ccolor定义为白色 Lambertian 表面朝向光的反射辐射(n = lc)。这是一个直观的创作定义,因为光的颜色直接对应于它的视觉效果。
通过这些定义,可以将定向光作为将区域光的大小缩小到零,同时保持clight值的极限情况。在这种情况下,反射率方程式(上图公式)中的积分可简化为单个BRDF评估,这大大降低了计算成本:
点积(n·l)通常被clamp为零,这是一种跳过表面下光线贡献的便捷方法:
精准光源可以类似地处理。唯一的区别是,区域光不需要原理,并且如公式(下图)所述,clight随距光的距离的平方成反比而下降。
在公式 :
中的π因子抵消了BRDF中经常出现的1 /π因子。此取消将除法运算移出了着色器,并使着色方程式更易于阅读。但是,在将学术论文中的BRDF应用于实时着色方程式时,必须小心。 通常,BRDF在使用前需要乘以π。
菲涅耳反射(Fresnel Reflflectance)
物体的表面是周围介质(通常是空气)与物体的物质之间的界面。光与两种物质之间的平面界面的相互作用遵循Augustin-Jean菲涅耳( Fresnel)(1788–1827)提出的菲涅耳方程(Fresnel equations)。菲涅耳方程需要遵循几何光学假设的平坦界面。 换句话说,假定该表面在尺寸为1个光波长和100个波长之间不具有任何不规则性。小于此范围的不规则度对光线没有影响,较大的不规则度有效地倾斜了表面,但不影响其局部平整度。
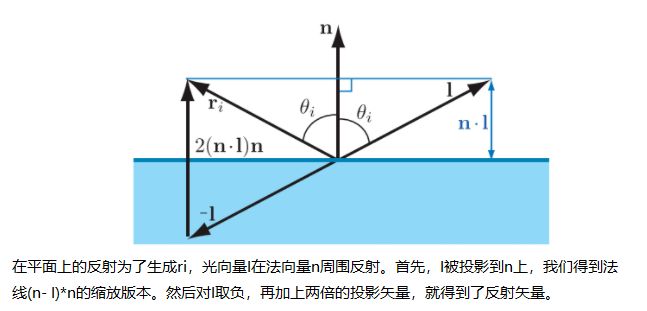
光在平面上的入射分裂成反射部分和折射部分。反射光的方向(由向量ri表示)与表面法线n形成与入射方向l相同的角度(θi)。 反射向量ri可以从n和l计算:
见下图。 菲涅耳反射率(Fresnel reflectance)F描述了反射的光量(作为入射光的一部分),菲涅耳反射率F取决于入射角θi。
反射和折射受两种物质在平面两侧的折射率的影响。我们将继续使用该讨论中的符号。 值n1是入射光和反射光在界面“上方”传播的物质的折射率,而n2是折射光传播在界面“下方”传播的物质的折射率。
菲涅耳方程描述了F对θi,n1和n2的依赖性。 我们将介绍它们的重要特征,而不是介绍有些复杂的方程式本身。
反射扩展(External Reflection)
当n1
对于给定的物质,菲涅耳方程可以解释为定义反射函数F(θi),仅取决于入射光角度。 原则上,F(θi)的值在可见光谱范围内连续变化。 出于渲染目的,其值被视为RGB矢量。 函数F(θi)具有以下特征:
• 当θi= 0°时,光垂直于表面(l = n),则F(θi)的值是物质的属性。 可以将该值F0视为物质的特征镜面反射颜色。 θi=0◦的情况称为法线入射。
• 随着θi的增加和光以越来越大的掠射角度射向表面,F(θi)的值将趋于增加,在θi= 90°时,所有频率(白色)的值都达到1。
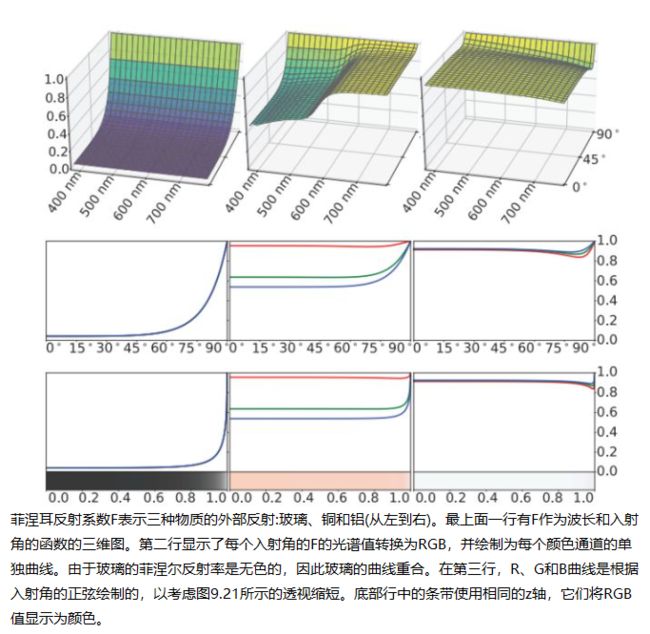
下图显示了几种物质的F(θi)函数,以几种不同的方式可视化。 曲线是高度非线性的,直到θi= 75°左右才变化,然后迅速变为1。从F0到1的增加大部分是单调的,尽管有些物质(例如,下图中的铝)在变成白色之前略有下降。
在镜面反射的情况下,出射或视角与入射角相同。 这意味着与入射光成一定角度的表面(θi值接近90°)也与眼睛成一定角度。因此,反射率的增加主要出现在物体的边缘。此外,从相机的角度来看,反射率增加最强的部分表面被缩短,因此它们占据的像素数量相对较少。为了显示菲涅耳曲线的不同部分与它们的视觉突出程度成比例,下图和上图的下半部分的菲涅耳反射率曲线图和颜色条是针对sin(θi)而不是直接针对θi绘制的。
下图说明了为什么sin(θi)是为此目的选择合适的轴的原因。
从这一点出发,对于菲涅耳函数,我们通常使用符号F(n,l)代替F(θi),以强调所涉及的向量。回想一下θi是向量n和l之间的角度。 当菲涅耳函数作为BRDF的一部分并入时,表面法线n通常会替换为不同的向量。
在渲染出版物中,在掠射角处反射率的增加通常称为菲涅耳效应(在其他领域,该术语与无线电波的传输具有不同的含义)。通过简短的实验,您可以亲自看到菲涅耳效果。拿起智能手机,坐在明亮的地方,例如电脑显示器前。 在不打开手机的情况下,首先将手机靠近您的胸部,低头看一下它,然后稍微倾斜一下角度,以使其屏幕反映出显示器。 显示器在电话屏幕上的反射应该相对较弱。这是因为玻璃的法向入射反射率非常低。 这是因为玻璃的法向入射反射率非常低。 现在抬起智能手机,使其大致位于您的眼睛和显示器之间,然后再次倾斜其屏幕以反射显示器。 现在,显示器在电话屏幕上的反射应几乎与显示器本身一样明亮。
除了其复杂性之外,菲涅尔方程还具有其他属性,这使得它们难以直接用于渲染。 它们需要在可见光谱上采样的折射率值,并且这些值可能是复数。图9.20中的曲线提出了一种基于特征镜面反射色F0的更简单方法。 Schlick给出菲涅耳反射率的近似值:
此功能是白色和F0之间的RGB插值。 尽管有这种简单性,但近似值还是相当准确的。
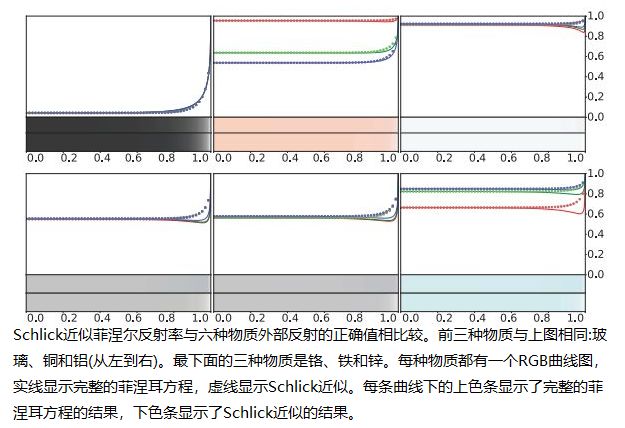
下图包含几种与Schlick曲线不同的物质,在变成白色之前就表现出明显的“凹陷”。实际上,之所以选择最下行的物质,是因为它们与Schlick近似值有很大的差异。即使对于这些物质,所产生的误差也非常微妙,如图中每个图底部的颜色条所示。 在极少数情况下,准确捕捉此类材料的行为很重要,可以使用Gulbrandsen给出的替代近似值。
尽管此近似值在计算上比Schlick的昂贵,但它可以与金属的整个Fresnel方程紧密匹配。 一个更简单的选择是修改Schlick的近似值,以允许将最终项提高到5以外的幂(如下公式所示)。这将在90°处将过渡的“清晰度”更改为白色,这可能会导致更接近的匹配。 Lagarde总结了菲涅耳方程和它们的一些近似。
使用Schlick近似值时,F0是控制菲涅耳反射率的唯一参数。 这很方便,因为F0在[0,1]中具有有效定义的有效值范围,易于使用标准的颜色选择界面进行设置,并且可以使用为颜色设计的纹理格式进行纹理处理。此外,F0的参考值可用于许多实际材料。 折射率也可以用于计算F0。 通常假设n1 = 1,这是空气折射率的近似值,并使用n代替n2表示物体的折射率。 这种简化给出以下方程式:
如果使用(复数)结果的大小,则该公式甚至适用于复数值折射率(例如金属的折射率)。 如果折射率在可见光谱范围内有显着变化,则计算F0的准确RGB值首先需要在密集的波长采样中计算F0,然后使用第8.1.3节中描述的方法将所得的光谱矢量转换为RGB值。
在某些应用中,使用更一般的Schlick近似形式:
这提供了对菲涅耳曲线在90◦时跃迁的颜色的控制,以及跃迁的“锐度。这种更一般的形式的使用通常是出于对艺术控制的渴望,但是在某些情况下,它也可以帮助匹配物理现实。如上所述,修改功率可以导致更接近某些材料。同样,将F90设置为除白色以外的其他颜色可以帮助匹配菲涅耳方程式无法很好描述的材料,例如被细小灰尘覆盖的表面具有单个光波长大小的颗粒。
典型的菲涅耳反射值(Typical Fresnel Reflflectance Values)
物质按其光学性质分为三大类。 有电介质(dielectrics),它们是绝缘体;金属,它们是导体;半导体,它们的性质介于介质和金属之间。
介质的菲涅耳反射值(Fresnel Reflectance Values for Dielectrics)
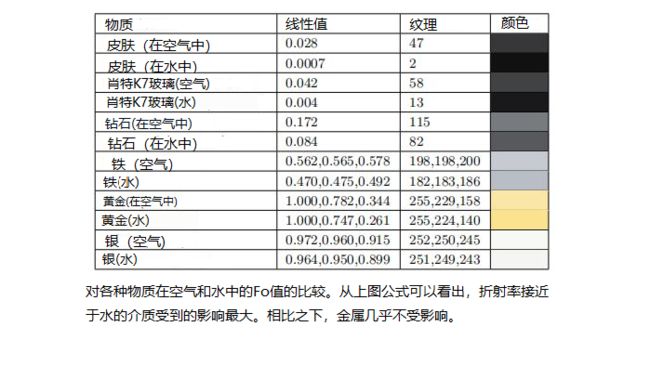
日常生活中遇到的大多数材料是电介质,例如玻璃,皮肤,木材,头发,皮革,塑料,石材和混凝土。水也是电介质。 最后这一点可能令人惊讶,因为在日常生活中已知水可以导电,但是这种导电性是由于各种杂质引起的。电介质的F0值很低,通常为0.06或更低。 法向入射时的这种低反射率使得菲涅耳效应对于电介质尤其明显。电介质的光学特性很少会在可见光谱范围内变化很大,从而导致无色反射率值。 下表列出了几种常用电介质的F0值。这些值是标量而不是RGB,因为这些材料的RGB通道没有显着差异。 为方便起见,下表包含线性值以及使用sRGB传递函数(通常在纹理绘画应用程序中使用的形式)编码的8位值。
其他电介质的F0值可以通过查看表中的类似物质来推断。 对于未知的电介质,0.04是合理的默认值,与大多数常用材料相差不大。
一旦光传输到电介质中,它可能会进一步散射或吸收。
金属的菲涅耳反射值(Fresnel Reflectance Values for Metals)
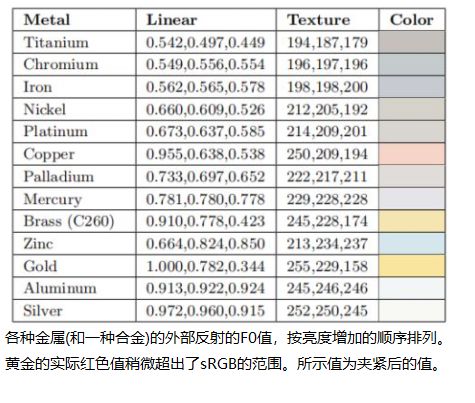
金属的F0值很高-几乎总是0.5或更高。 某些金属的光学特性会在可见光谱范围内变化,从而导致彩色反射率值。 下表列出了几种金属的F0值。
与上表相似,下表具有线性值以及用于纹理化的8位sRGB编码值。但是,由于许多金属的菲涅耳反射率是彩色的,因此这里给出RGB值。 这些RGB值是使用sRGB(和Rec.709)原色和白点定义的。黄金的F0值有些不同寻常。 它是最强的颜色,红色通道值略高于1(它只是勉强在sRGB/Rec 709色域之外),蓝色通道值特别低(下表中唯一明显低于0.5的值)。 从表中的位置可以看出,它也是最亮的金属之一,并按亮度增加的顺序进行排序。 黄金明亮而色彩鲜艳的反射率可能有助于其在整个历史上的独特文化和经济意义。
回想一下,金属会立即吸收任何透射光,因此它们不会表现出任何次表面散射或透明性。 金属的所有可见颜色都来自F0。
半导体的菲涅耳反射值(Fresnel Reflectance Values for Semiconductors)
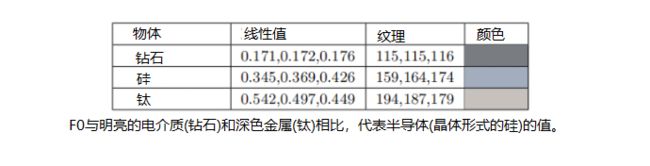
正如人们所期望的那样,半导体的F0值介于最亮的电介质和最暗的金属之间,如下表所示。在实践中很少需要渲染这样的物质,因为大多数渲染的场景不会散布有结晶硅块。 出于实际目的,应避免F0值在0.2到0.45之间的范围,除非您有意尝试对奇异或不切实际的材料进行建模。
水中菲涅耳反射率值(Fresnel Reflectance Values in Water )
在讨论外部反射率时,我们假设渲染的表面被空气包围。 否则,反射率将改变,因为它取决于界面两侧的折射率之比。 如果我们不再假设n1 = 1,则需要用相对折射率n1 / n2代替公式9.17中的n。 这将产生以下更一般的公式:
n1 = 1时最常遇到的情况是渲染水下场景时。 由于水的折射率是空气的约1.33倍,因此F0的值在水下有所不同。 如下表所示,电介质的这种作用比金属强。
参数化菲涅耳值(Parameterizing Fresnel Values)
经常使用的参数化将镜面反射颜色F0和漫反射颜色ρss结合在一起(漫反射颜色将在9.9节中进一步讨论)。此参数化利用了以下观察优势:金属没有漫反射的颜色,并且电介质具有有限的F0可能值集,并且它包括RGB表面颜色Csurf和标量参数m,称为“金属”或“金属度”。如果m = 1,则将F0设置为csurf,并将ρss设置为黑色。 如果m = 0,则将F0设置为电介质的值(常数或由附加参数控制),并将ρss设置为Csurf。
“金属度”参数首先出现在Brown大学使用的早期着色模型中,并且Pixar首次将其当前形式的参数化用于电影Wall-E。对于Wreck-It Ralph以后的Disney动画电影中使用的Disney原理着色模型,Burley添加了附加的标量“镜面”参数,以将电介质F0控制在有限范围内。
对于那些使用这种金属性参数化而不是直接使用F0和ρss的渲染应用程序,其动机包括用户方便以及节省纹理或G缓冲区存储。
使用金属性有一些缺点。 它不能表示某些类型的材料,例如带有F0值的涂层电介质。 瑕疵会出现在金属和电介质之间的边界上。
一些实时应用程序使用的另一个参数化技巧是利用以下事实:在特殊的抗反射涂层之外,没有材料的F0值低于0.02。 这个技巧被用来抑制代表空洞或空洞的表面积中的镜面高光。 代替使用单独的镜面光遮挡纹理,使用低于0.02的F0值来“关闭”菲涅耳边缘增亮。
内反射(Internal Reflection)
尽管在渲染中更经常遇到外部反射,但是内部反射有时也很重要。 当n1> n2时会发生内部反射。 换句话说,当光在透明物体的内部传播并且“从内部”遇到物体的表面时,就会发生内部反射。 参见下图。
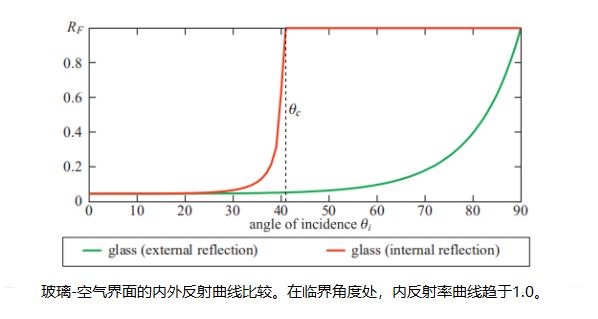
Snell’s 定律表明,对于内部反射,sinθt> sinθi。 由于这些值都在0°至90°之间,因此这种关系也意味着θt>θi,如上图所示。在外反射的情况下,情况恰好相反—将此行为与下图进行比较。这种差异是了解内部反射和外部反射如何不同的关键。 在外反射中,对于sinθi的每个可能值(介于0和1之间),存在一个有效(较小)的sinθt值。对于内反射而言,情况并非如此。对于大于临界角θc的θi值,Snell’s 定律暗示sinθt> 1,这是不可能的。 现实情况是没有θt。 当θi>θc时,不会发生透射,并且所有入射光都会被反射。 这种现象称为全内反射(total internal reflection)。
菲涅耳方程是对称的,从某种意义上说,可以切换入射矢量和透射矢量,并且反射率保持不变。 结合斯涅尔定律,这种对称性意味着用于内部反射的F(θi)曲线将类似于用于外部反射的曲线的“压缩”形式。 对于这两种情况,F0的值是相同的,内部反射曲线在θc达到完美反射率,而不是在90◦。如下图所示,该图还表明,在内部反射的情况下,平均而言,反射率更高。 例如,这就是为什么在水下看到的气泡具有高度反射性的银色外观的原因。
内部反射仅在电介质中发生,因为金属和半导体会迅速吸收在其内部传播的所有光。 由于电介质具有实值折射率,因此从折射率或从F0计算临界角非常简单:
下图公式中所示的Schlick近似对于外部反射是正确的。通过将透射角θt替换为θi,可用于内部反射。如果已经计算出传输方向矢量t(例如,用于渲染折射),则可以将其用于查找θt。 否则,可以使用斯涅尔定律从θi计算θt,但这很昂贵并且需要折射率,而这可能是不可用的。
conclusion:
本文主要说明了计算机显示器屏幕颜色混合的原理(CIE),深度解析了光与一些介质的交互传播性质以及一些光照渲染的介绍。
光强度是单位立体角的辐射能量
辐射度是单位面积流出的光通量
辐照度是单位面积流入的光通量
光强度 = 光亮度 * 单位面积 * 入射角余弦
辐照度 = 光亮度 * 入射角余弦 * 单位立体角(方向入射光的方向)
辐射度 = 光亮度 * 入射角余弦 * 单位立体角(方向反射光的方向)
--------------------------------------------------------------------------------------------------
BRDF规定的是辐照度和光亮度关系:
光亮度 = BRDF * 辐照度
Reference:
https://www.zhihu.com/zvideo/1495357723130269696?utm_source=qq&utm_medium=social&utm_oi=1194640585280262144
https://zhuanlan.zhihu.com/p/392935292
https://github.com/QianMo/Real-Time-Rendering-3rd-CN-Summary-Ebook
physically based rendering
real time rendering 4th
对于给定的物质,菲涅耳方程可以解释为定义反射函数F(θi),仅取决于入射光角度。 原则上,F(θi)的值在可见光谱范围内连续变化。 出于渲染目的,其值被视为RGB矢量。 函数F(θi)具有以下特征:
• 当θi= 0°时,光垂直于表面(l = n),则F(θi)的值是物质的属性。 可以将该值F0视为物质的特征镜面反射颜色。 θi=0◦的情况称为法线入射。
• 随着θi的增加和光以越来越大的掠射角度射向表面,F(θi)的值将趋于增加,在θi= 90°时,所有频率(白色)的值都达到1。
下图显示了几种物质的F(θi)函数,以几种不同的方式可视化。 曲线是高度非线性的,直到θi= 75°左右才变化,然后迅速变为1。从F0到1的增加大部分是单调的,尽管有些物质(例如,下图中的铝)在变成白色之前略有下降。
在镜面反射的情况下,出射或视角与入射角相同。 这意味着与入射光成一定角度的表面(θi值接近90°)也与眼睛成一定角度。因此,反射率的增加主要出现在物体的边缘。此外,从相机的角度来看,反射率增加最强的部分表面被缩短,因此它们占据的像素数量相对较少。为了显示菲涅耳曲线的不同部分与它们的视觉突出程度成比例,下图和上图的下半部分的菲涅耳反射率曲线图和颜色条是针对sin(θi)而不是直接针对θi绘制的。
下图说明了为什么sin(θi)是为此目的选择合适的轴的原因。
从这一点出发,对于菲涅耳函数,我们通常使用符号F(n,l)代替F(θi),以强调所涉及的向量。回想一下θi是向量n和l之间的角度。 当菲涅耳函数作为BRDF的一部分并入时,表面法线n通常会替换为不同的向量。
在渲染出版物中,在掠射角处反射率的增加通常称为菲涅耳效应(在其他领域,该术语与无线电波的传输具有不同的含义)。通过简短的实验,您可以亲自看到菲涅耳效果。拿起智能手机,坐在明亮的地方,例如电脑显示器前。 在不打开手机的情况下,首先将手机靠近您的胸部,低头看一下它,然后稍微倾斜一下角度,以使其屏幕反映出显示器。 显示器在电话屏幕上的反射应该相对较弱。这是因为玻璃的法向入射反射率非常低。 这是因为玻璃的法向入射反射率非常低。 现在抬起智能手机,使其大致位于您的眼睛和显示器之间,然后再次倾斜其屏幕以反射显示器。 现在,显示器在电话屏幕上的反射应几乎与显示器本身一样明亮。
除了其复杂性之外,菲涅尔方程还具有其他属性,这使得它们难以直接用于渲染。 它们需要在可见光谱上采样的折射率值,并且这些值可能是复数。图9.20中的曲线提出了一种基于特征镜面反射色F0的更简单方法。 Schlick给出菲涅耳反射率的近似值:
此功能是白色和F0之间的RGB插值。 尽管有这种简单性,但近似值还是相当准确的。
下图包含几种与Schlick曲线不同的物质,在变成白色之前就表现出明显的“凹陷”。实际上,之所以选择最下行的物质,是因为它们与Schlick近似值有很大的差异。即使对于这些物质,所产生的误差也非常微妙,如图中每个图底部的颜色条所示。 在极少数情况下,准确捕捉此类材料的行为很重要,可以使用Gulbrandsen给出的替代近似值。
尽管此近似值在计算上比Schlick的昂贵,但它可以与金属的整个Fresnel方程紧密匹配。 一个更简单的选择是修改Schlick的近似值,以允许将最终项提高到5以外的幂(如下公式所示)。这将在90°处将过渡的“清晰度”更改为白色,这可能会导致更接近的匹配。 Lagarde总结了菲涅耳方程和它们的一些近似。
使用Schlick近似值时,F0是控制菲涅耳反射率的唯一参数。 这很方便,因为F0在[0,1]中具有有效定义的有效值范围,易于使用标准的颜色选择界面进行设置,并且可以使用为颜色设计的纹理格式进行纹理处理。此外,F0的参考值可用于许多实际材料。 折射率也可以用于计算F0。 通常假设n1 = 1,这是空气折射率的近似值,并使用n代替n2表示物体的折射率。 这种简化给出以下方程式:
如果使用(复数)结果的大小,则该公式甚至适用于复数值折射率(例如金属的折射率)。 如果折射率在可见光谱范围内有显着变化,则计算F0的准确RGB值首先需要在密集的波长采样中计算F0,然后使用第8.1.3节中描述的方法将所得的光谱矢量转换为RGB值。
在某些应用中,使用更一般的Schlick近似形式:
这提供了对菲涅耳曲线在90◦时跃迁的颜色的控制,以及跃迁的“锐度。这种更一般的形式的使用通常是出于对艺术控制的渴望,但是在某些情况下,它也可以帮助匹配物理现实。如上所述,修改功率可以导致更接近某些材料。同样,将F90设置为除白色以外的其他颜色可以帮助匹配菲涅耳方程式无法很好描述的材料,例如被细小灰尘覆盖的表面具有单个光波长大小的颗粒。
典型的菲涅耳反射值(Typical Fresnel Reflflectance Values)
物质按其光学性质分为三大类。 有电介质(dielectrics),它们是绝缘体;金属,它们是导体;半导体,它们的性质介于介质和金属之间。
介质的菲涅耳反射值(Fresnel Reflectance Values for Dielectrics)
日常生活中遇到的大多数材料是电介质,例如玻璃,皮肤,木材,头发,皮革,塑料,石材和混凝土。水也是电介质。 最后这一点可能令人惊讶,因为在日常生活中已知水可以导电,但是这种导电性是由于各种杂质引起的。电介质的F0值很低,通常为0.06或更低。 法向入射时的这种低反射率使得菲涅耳效应对于电介质尤其明显。电介质的光学特性很少会在可见光谱范围内变化很大,从而导致无色反射率值。 下表列出了几种常用电介质的F0值。这些值是标量而不是RGB,因为这些材料的RGB通道没有显着差异。 为方便起见,下表包含线性值以及使用sRGB传递函数(通常在纹理绘画应用程序中使用的形式)编码的8位值。
其他电介质的F0值可以通过查看表中的类似物质来推断。 对于未知的电介质,0.04是合理的默认值,与大多数常用材料相差不大。
一旦光传输到电介质中,它可能会进一步散射或吸收。
金属的菲涅耳反射值(Fresnel Reflectance Values for Metals)
金属的F0值很高-几乎总是0.5或更高。 某些金属的光学特性会在可见光谱范围内变化,从而导致彩色反射率值。 下表列出了几种金属的F0值。
与上表相似,下表具有线性值以及用于纹理化的8位sRGB编码值。但是,由于许多金属的菲涅耳反射率是彩色的,因此这里给出RGB值。 这些RGB值是使用sRGB(和Rec.709)原色和白点定义的。黄金的F0值有些不同寻常。 它是最强的颜色,红色通道值略高于1(它只是勉强在sRGB/Rec 709色域之外),蓝色通道值特别低(下表中唯一明显低于0.5的值)。 从表中的位置可以看出,它也是最亮的金属之一,并按亮度增加的顺序进行排序。 黄金明亮而色彩鲜艳的反射率可能有助于其在整个历史上的独特文化和经济意义。
回想一下,金属会立即吸收任何透射光,因此它们不会表现出任何次表面散射或透明性。 金属的所有可见颜色都来自F0。
半导体的菲涅耳反射值(Fresnel Reflectance Values for Semiconductors)
正如人们所期望的那样,半导体的F0值介于最亮的电介质和最暗的金属之间,如下表所示。在实践中很少需要渲染这样的物质,因为大多数渲染的场景不会散布有结晶硅块。 出于实际目的,应避免F0值在0.2到0.45之间的范围,除非您有意尝试对奇异或不切实际的材料进行建模。
水中菲涅耳反射率值(Fresnel Reflectance Values in Water )
在讨论外部反射率时,我们假设渲染的表面被空气包围。 否则,反射率将改变,因为它取决于界面两侧的折射率之比。 如果我们不再假设n1 = 1,则需要用相对折射率n1 / n2代替公式9.17中的n。 这将产生以下更一般的公式:
n1 = 1时最常遇到的情况是渲染水下场景时。 由于水的折射率是空气的约1.33倍,因此F0的值在水下有所不同。 如下表所示,电介质的这种作用比金属强。
参数化菲涅耳值(Parameterizing Fresnel Values)
经常使用的参数化将镜面反射颜色F0和漫反射颜色ρss结合在一起(漫反射颜色将在9.9节中进一步讨论)。此参数化利用了以下观察优势:金属没有漫反射的颜色,并且电介质具有有限的F0可能值集,并且它包括RGB表面颜色Csurf和标量参数m,称为“金属”或“金属度”。如果m = 1,则将F0设置为csurf,并将ρss设置为黑色。 如果m = 0,则将F0设置为电介质的值(常数或由附加参数控制),并将ρss设置为Csurf。
“金属度”参数首先出现在Brown大学使用的早期着色模型中,并且Pixar首次将其当前形式的参数化用于电影Wall-E。对于Wreck-It Ralph以后的Disney动画电影中使用的Disney原理着色模型,Burley添加了附加的标量“镜面”参数,以将电介质F0控制在有限范围内。
对于那些使用这种金属性参数化而不是直接使用F0和ρss的渲染应用程序,其动机包括用户方便以及节省纹理或G缓冲区存储。
使用金属性有一些缺点。 它不能表示某些类型的材料,例如带有F0值的涂层电介质。 瑕疵会出现在金属和电介质之间的边界上。
一些实时应用程序使用的另一个参数化技巧是利用以下事实:在特殊的抗反射涂层之外,没有材料的F0值低于0.02。 这个技巧被用来抑制代表空洞或空洞的表面积中的镜面高光。 代替使用单独的镜面光遮挡纹理,使用低于0.02的F0值来“关闭”菲涅耳边缘增亮。
内反射(Internal Reflection)
尽管在渲染中更经常遇到外部反射,但是内部反射有时也很重要。 当n1> n2时会发生内部反射。 换句话说,当光在透明物体的内部传播并且“从内部”遇到物体的表面时,就会发生内部反射。 参见下图。
Snell’s 定律表明,对于内部反射,sinθt> sinθi。 由于这些值都在0°至90°之间,因此这种关系也意味着θt>θi,如上图所示。在外反射的情况下,情况恰好相反—将此行为与下图进行比较。这种差异是了解内部反射和外部反射如何不同的关键。 在外反射中,对于sinθi的每个可能值(介于0和1之间),存在一个有效(较小)的sinθt值。对于内反射而言,情况并非如此。对于大于临界角θc的θi值,Snell’s 定律暗示sinθt> 1,这是不可能的。 现实情况是没有θt。 当θi>θc时,不会发生透射,并且所有入射光都会被反射。 这种现象称为全内反射(total internal reflection)。
菲涅耳方程是对称的,从某种意义上说,可以切换入射矢量和透射矢量,并且反射率保持不变。 结合斯涅尔定律,这种对称性意味着用于内部反射的F(θi)曲线将类似于用于外部反射的曲线的“压缩”形式。 对于这两种情况,F0的值是相同的,内部反射曲线在θc达到完美反射率,而不是在90◦。如下图所示,该图还表明,在内部反射的情况下,平均而言,反射率更高。 例如,这就是为什么在水下看到的气泡具有高度反射性的银色外观的原因。
内部反射仅在电介质中发生,因为金属和半导体会迅速吸收在其内部传播的所有光。 由于电介质具有实值折射率,因此从折射率或从F0计算临界角非常简单:
下图公式中所示的Schlick近似对于外部反射是正确的。通过将透射角θt替换为θi,可用于内部反射。如果已经计算出传输方向矢量t(例如,用于渲染折射),则可以将其用于查找θt。 否则,可以使用斯涅尔定律从θi计算θt,但这很昂贵并且需要折射率,而这可能是不可用的。
conclusion:
本文主要说明了计算机显示器屏幕颜色混合的原理(CIE),深度解析了光与一些介质的交互传播性质以及一些光照渲染的介绍。
光强度是单位立体角的辐射能量
辐射度是单位面积流出的光通量
辐照度是单位面积流入的光通量
光强度 = 光亮度 * 单位面积 * 入射角余弦
辐照度 = 光亮度 * 入射角余弦 * 单位立体角(方向入射光的方向)
辐射度 = 光亮度 * 入射角余弦 * 单位立体角(方向反射光的方向)
--------------------------------------------------------------------------------------------------
BRDF规定的是辐照度和光亮度关系:
光亮度 = BRDF * 辐照度
Reference:
https://www.zhihu.com/zvideo/1495357723130269696?utm_source=qq&utm_medium=social&utm_oi=1194640585280262144
https://zhuanlan.zhihu.com/p/392935292
https://github.com/QianMo/Real-Time-Rendering-3rd-CN-Summary-Ebook
physically based rendering
real time rendering 4th