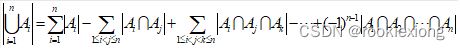集合论知识总结——集合及其运算

   第一章 集合及其运算 

§1 集合的基本概念

§2 子集、集合的相等

§3 集合的基本运算

§4 余集运算

§5 笛卡儿乘积

§6 有限集合的基数

第一章 集合及其运算

§1 集合的基本概念

一般地，把一些确定的，可以区分的事物放在一起组成一个整体称为集合，简称集。

集合的特点：1.任意性(不能说所有集合的集合)；2.不能重复；3.无序性；4.确定性。

三个原始概念：集合、元素、属于。

空集和全集：不含任何元素的集合称为空集，记为¢。符号化表示为：¢={x|x≠x}

在给定的问题中，所考虑的所有事物的集合称为全集，记为S。符号化表示为：S={x|x=x}

单元集：仅含有一个元素的集合称为单元集。

注意：｛x｝与x的区别。  x——元素，｛x｝——集合。

§2 子集、集合的相等

子集：设A,B是两个集合，若集合A中的每个元素都是B的元素，则称A是B的子集合简称子集，这时也说A包含在B里。A是B的子集记为(或B包含着A)。

。等价地有：不在中的元素必不在中。

集合不包含:若A不是B的子集，则记为A⊈B (A不包含在B里)

真包含：设A,B为两个集合，若且，则称A是B的真子集，记为A⊂B。        。集合真包含等价形式：

注意：“∈”与“⊂”的区别

集合相等：设A,B是两个集合，若A属于B且B属于A，则称A与B相等。并记为A＝B。即

A=B等价于A属于B且B属于A。（证明题）

集合不相等：若集合A和集合B不相等，则记为A≠B。即A≠B等价于A⊈B或B⊈A。

集族：以集合为元素的构成集合称为集族。

幂集：集合S的所有子集（包括空集¢及S本身-易错）形成的集族称为S的幂集，记为或P(S)。

说明：

(1)S有n个元素，则S有个子集。这就是为什么采用符号的原因。

(2) ¢和{¢}的区别与联系

 区别：¢:空集， {¢}:一个集族，这个集族只有一个元素，就是空集¢，因此 ¢≠{¢}。

 联系：¢{¢}， ¢∈{¢}。而A≠¢，A∈{A}成立， A{A}不成立。

性质：（1）空集¢是任一集合的子集;（2）空集¢是唯一的。

§3 集合的基本运算

并运算：设A，B是任意两个集合，则由至少属于集合A与集合B之一的一切元素组成的集合，称为集合A与B的并集，记为A∪B。

交运算：设A，B是任意两个集合，则由既属于A又属于B的一切元素组成的集合，称为集合A与集合B的交集，记为A∩B 。

差运算：设A，B是两个任意集合，则由属于A但不属B的一切元素组成的集合，称为A与B的差集，记为A\B（或A-B）。即 A\B={x|xA但xB}

对称差：设A，B是两个任意集合，则差集A\B与B\A的并集称为集合A与集合B的对称差，记为A∆B。即A∆B=(A\B)⋃(B\A)

说明：

1.当两个集合的交集为空集时,则称它们是不相交的；    

2.两两不相交；设A1,A2,…,An 是n个集合，若"Ai,Aj (i≠j)有Ai∩Aj=¢,则称A1,A2,…,An是两两不相交的。

3.两个集合并、交运算可以推广到多个集合上去。

性质（并、交运算以及它们之间的关系）：

定理1.2 设A,B,C是三个任意集合，S为全集，则

1). 交换律成立，即A∪B=B∪A、A∩B=B∩A、A∆B=B∆A

2). 结合律成立，即(A∪B)∪C=A∪(B∪C)、(A∩B)∩C=A∩(B∩C)、(A∆B)∆C=AD(B∆C)

3). 幂等律成立，即A∪A=A、A∩A=A、ADA=¢

注：差运算交换律、结合律、幂等律都不成立

4). ¢∪A=A、¢∩A=¢、A∆¢=A, A∆S=S\A=

5). S∪A=S、S∩A=A

6). A∪B=BóAÍB、A∩B=AóAÍB

基本运算间的关系(分配律和吸收律)

定理3 设A,B,C是三个任意集合，则

1.A∪(B∩C)=(A∪B)∩(A∪C)        2.A∩(B∪C)=(A∩B)∪(A∩C)

3.A∩(B\C)=(A∩B)\(A∩C)              4.A∩(B∆C) =(A∩B)D(A∩C)

5.A∪(A∩B)=A                              6.A∩(A∪B)=A

7.A∆(A∆B)= B                               8.A\B=A\(A∩B)

9.A\B=A∩

10.A\B=¢等价于AÍB                      11.(A\B)∪B=A等价于B⊆A

§4 余集运算

余集：设S是集合，A⊆S，则差集S\A称为集合A对集合S的余集，记为。即 = S\A

并、交运算与余集的关系

设A,B是两个任意集合,则

1.(A∪B)C= AC∩BC                            2.(A∩B)^C= ∪                       

3.若A⊆B，则AC ÊBC                         4.()^C=A

推广到多个集合：

对偶原理：若有关集合的并、交及余集运算的某一关系式成立，则将式中记号∪、∩、⊆、⊇分别换成∩、∪、⊇、⊆，等号“=”不变，并将式中每一个集合换成它的余集。由此得到的新的关系式也一定成立。

§5 笛卡儿乘积

序对：两个对象a和b（允许a＝b）按着一定的次序排列的整体称为一个二元组或序对。

序对与集合的区别：

序对是由有次序的两个对象组成的，因此序对与含有两个对象的集合有区别。

笛卡儿乘积：

1.设A与B为两个任意集合，集合{(a,b)|aA，bB}为A与B的笛卡儿乘积，记为A×B。

2.设A1,A2,…,An 为 n(n≥3)个集合，则集合{(a1,a2,…,an)|aiAi,i=1,2,…,n}称为A1,A2,…,An的笛卡儿乘积，并记为 A1×A2×…×An。于是A1×A2×…×An= {(a1,a2,…,an)|aiAi,i=1,2,…,n}，当A1=A2=…=An=A时， A1×A2×…×An记为A^n。

A×B=B×A充要条件是下列三个条件至少一个成立: (1) A=¢；(2) B=¢；(3) A=B。

笛卡儿乘积一般不满足交换律；不满足封闭性；不满足结合律；

若A,B,C都不是空集时，结合律不成立。即  (A×B)×C≠A×(B×C)

若A,B,C中有一个是空集¢时，则上式成立，即  (A×B)×C＝A×(B×C)= ¢

性质(笛卡儿乘积运算与并、交、差运算的关系)

定理1 设A,B,C是三个集合，则

（1） A×(B∪C)=(A×B)∪(A×C)     （2） A×(B∩C)=(A×B)∩(A×C)

（3） A×(B\C)=(A×B)\(A×C)          （4） A×(B∆C)=(A×B)∆(A×C)

定理2 设A,B,C是三个集合，C≠¢，则A⊆B等价于A×C⊆B×C

定理3 设A,B,C,D为集合，则A×B⊆C×D等价于A⊆C且B⊆D

n元组：n元组是n个对象按一定顺序排列组成的整体。若第1个分量为x1，第2个分量为x2,…,第n个分量为xn，则这个n元组就记为:（x1,x2,…,xn）。

§6 有限集合的基数

一一对应：

1.设A和B是两个有限集合,若存在一个法则j使得"xA，根据法则j在B中有唯一的y与x对应，这个y常记为j(x)；而且,"yB，存在A中的唯一的x，使得x在j下对应于y。这个法则j称为从A到B的一个一一对应。

2.设A,B是两个集合，若A×B的子集f满足下列条件：

(1)"xA,存在唯一的yB,使得(x,y)f (f(x)=y);

(2)"yB,存在唯一的xA,使得(x,y)f (f(x)=y)。

则称f是集合A到B的一个一一对应。

有限集合及其基数：设A是一个集合,若A=¢或A≠¢且存在一个自然数n,使得A与集合{1,2,…,n}间存在一个一一对应，则称集合A为有限集。数n称为集合A的基数，记为|A|

说明：1.空集¢的基数定义为数0，即|¢|=0。2.若A不是有限集合，则A为无限集合。

基数的比较：设A,B是两个集合，若A与B的一个真子集之间有一个一一对应，但A与B之间不存在一一对应，则称集合A的基数|A|小于集合B的基数|B|，记为 |A|<|B|。

集合基数的性质：

定理1设A,B,C是三个有限集合，则

（1）若A∩B=¢，则 |A∪B|=|A|+|B|；      （2）若A∩B≠¢，则 |A∪B|=|A|+|B|-|A∩B|；

（3）|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|；

（4）设S为有限集，A⊆S，则||=|S\A|=|S|-|A|；

（5）|A∆B|=|A|+|B|-2|A∆B|（A∆B=(A∪B)\(B∩A)); （6）|2^A|=2^|A| ;（7）|A×B|=|A|·|B|；

推广：| A1×A2×…×An |= |A1|·|A2|·…·|An|；

（8）|A∪B|≤|A|+|B|；  （9) |A∩B|≤min(|A|,|B|)；    (10) |A\B|≥|A|-|B|。

 逐步淘汰定理(容斥原理)

1).设A1,A2,…,An为n个两两不相交的有限集合，则

2).设A1,A2,…,An为n个有限集合，则

3).设A1,A2,…,An为有限集合S的子集，则