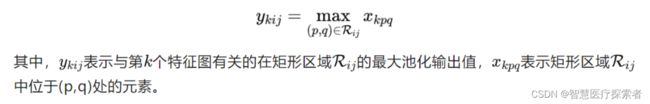深度学习中的池化

1 深度学习池化概述

1.1 什么是池化

池化层是卷积神经网络中常用的一个组件，池化层经常用在卷积层后边，通过池化来降低卷积层输出的特征向量，避免出现过拟合的情况。池化的基本思想就是对不同位置的特征进行聚合统计。池化层主要是模仿人的视觉系统对数据进行降维，用更高层次的特征表示图像。池化层一般没有参数，所以反向传播的时候，只需对输入参数求导，不需要进行权值更新。

池化操作的基本思想是将特征图划分为若干个子区域（一般为矩形），并对每个子区域进行统计汇总。池化操作的方式可以有很多种，比如最大池化（Max Pooling）、平均池化（Average Pooling）等。其中，最大池化操作会选取每个子区域内的最大值作为输出，而平均池化操作则会计算每个子区域内的平均值作为输出。

1.2 池化的作用

理论上来说，网络可以在不对原始输入图像执行降采样的操作，通过堆叠多个的卷积层来构建深度神经网络，如此一来便可以在保留更多空间细节信息的同时提取到更具有判别力的抽象特征。然而，考虑到计算机的算力瓶颈，通常都会引入池化层，来进一步地降低网络整体的计算代价，这是引入池化层最根本的目的。

池化层大大降低了网络模型参数和计算成本，也在一定程度上降低了网络过拟合的风险。概括来说，池化层主要有以下五点作用：

• 增大网络感受野

• 抑制噪声，降低信息冗余

• 降低模型计算量，降低网络优化难度，防止网络过拟合

• 使模型对输入图像中的特征位置变化更加鲁棒

1.3 池化核大小

池化窗口的大小，在PyTorch里池化核大小可以是一个整数或者一个元组，例如 kernel_size=2 或者 kernel_size=(2, 3)。

• 如果是一个整数，则表示高和宽方向上的池化窗口大小相同；
• 如果是一个元组，则第一个元素表示高方向上的池化窗口大小，第二个元素表示宽方向上的池化窗口大小。

1.4 步幅大小

用于指定池化窗口在高和宽方向上的步幅大小，可以是一个整数或者一个元组，例如 stride=2 或者 stride=(2, 3)。

• 如果是一个整数，则表示高和宽方向上的步幅大小相同；
• 如果是一个元组，则第一个元素表示高方向上的步幅大小，第二个元素表示宽方向上的步幅大小。

1.5 填充

池化层的填充（padding）可以控制池化操作在特征图边缘的行为，使得池化后的输出特征图与输入特征图大小相同或相近。

在池化操作时，如果输入特征图的尺寸不能被池化窗口的大小整除，那么最后一列或者最后一行的部分像素就无法被包含在池化窗口中进行池化，因此池化后的输出特征图尺寸会减小。

通过在输入特征图的边缘添加填充，可以使得池化操作在边缘像素处进行池化，避免了信息的丢失，并且保持了输出特征图的大小与输入特征图相同或相近。同时，填充也可以增加模型的稳定性，减少过拟合的风险。

需要注意的是，池化层的填充和卷积层的填充有所不同：

• 池化层的填充通常是指在输入特征图的边缘添加0值像素；
• 卷积层的填充是指在输入特征图的边缘添加0值像素或者复制边缘像素。

PyTorch里的填充大小可以是一个整数或者一个元组，例如 padding=1 或者 padding=(1, 2)。

• 如果是一个整数，则表示在高和宽方向上的填充大小相同；
• 如果是一个元组，则第一个元素表示高方向上的填充大小，第二个元素表示宽方向上的填充大小。默认为 0，表示不进行填充。

2 pytorch中的池化详解

2.1 Max Pooling(最大池化)

2.1.1 定义

最大池化(Max Pooling)是将输入的图像划分为若干个矩形区域，对每个子区域输出最大值。其定义如下：

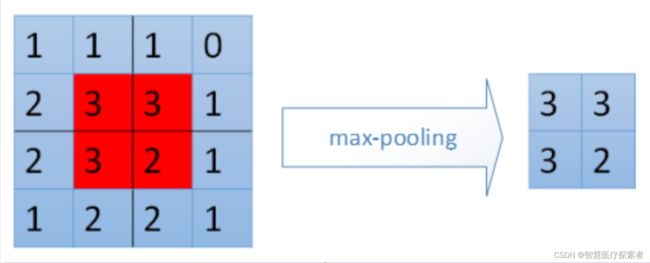
最大池化就是选取图像区域中的最大值作为该区域池化后的值。在前向传播过程中，选择图像区域中的最大值作为该区域池化后的值；在反向传播过程中，梯度通过前向传播过程时的最大值反向传播，其他位置的梯度为0。如下图所示，采用22的filters，步长stride=2，在原特征图44中提取特征得到右图2*2。

最大值池化的优点在于它能学习到图像的边缘和纹理结构。

对于最大池化，在前向传播计算时，是选取的每个区域中的最大值，这里需要记录下最大值在每个小区域中的位置。在反向传播时，只有那个最大值对下一层有贡献，所以将残差传递到该最大值的位置，区域内其余位置置零。具体过程如下图，其中4*4矩阵中非零的位置即为前边计算出来的每个小区域的最大值的位置。

2.1.2 pytorch中的最大池化

PyTorch中的最大池化函数：

torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)

• kernel_size (int or tuple)【必选】：max pooling 的窗口大小，当最大池化窗口是方形的时候，只需要一个整数边长即可；最大池化窗口不是方形时，要输入一个元组表 高和宽。

• stride (int or tuple, optional)【可选】：max pooling 的窗口移动的步长。默认值是 kernel_size

• padding (int or tuple, optional)【可选】：输入的每一条边补充0的层数

• dilation (int or tuple, optional)【可选】：一个控制窗口中元素步幅的参数

• return_indices (bool)【可选】：如果等于 True，会返回输出最大值的序号，对于上采样操作会有帮助

• ceil_mode (bool)【可选】：如果等于True，计算输出信号大小的时候，会使用向上取整，代替默认的向下取整的操作

torch.nn.MaxPool2d 和 torch.nn.functional.max_pool2d，在 pytorch 构建模型中，都可以作为最大池化层的引入，但前者为类模块，后者为函数，在使用上存在不同。

torch.nn.functional.max_pool2d(
	input, 
	kernel_size, 
	stride=None, 
	padding=0, 
	dilation=1, 
	ceil_mode=False, 
	return_indices=False
)

2.1.3 使用示例

• 张量池化

import torch

# 定义输入数据张量，大小为 (batch_size, channels, height, width)
input_tensor = torch.randn(2, 3, 16, 16)

# 定义最大池化层，kernel_size 为池化核大小，stride 为步幅
max_pool = torch.nn.MaxPool2d(kernel_size=2, stride=2)

# 对输入数据进行最大池化操作
output_tensor = max_pool(input_tensor)

# 输出池化前后的结果张量大小
print("input_tensor:", input_tensor.shape)
print("output_tensor:", output_tensor.shape)

运行结果显示：

input_tensor: torch.Size([2, 3, 16, 16])
output_tensor: torch.Size([2, 3, 8, 8])

输入大小为 (2,3,16,16)的张量， 然后定义了一个最大池化层，池化操作以后，
最后输出的张量大小是： torch.Size([2, 3, 8, 8])

• 图片池化

import torch
from PIL import Image
from torchvision.transforms import ToTensor
from torchvision.transforms.functional import to_pil_image
import matplotlib.pyplot as plt

# 读入示例图片并将其转换为 PyTorch 张量
img = Image.open('./data/lena.jpeg')
img_tensor = ToTensor()(img)

# 定义 MaxPool2d 函数，进行池化操作
max_pool = torch.nn.MaxPool2d(kernel_size=2, stride=2)
img_pool = max_pool(img_tensor.unsqueeze(0)).squeeze(0)

# 将池化后的张量转换为 PIL 图像并保存
img_pool_pil = to_pil_image(img_pool)

plt.subplot(121)
plt.imshow(img)
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(img_pool_pil)
plt.title('pool')
plt.axis('off')
plt.show()

运行结果显示：

2.1.4 总结

对于最大池化操作，只选择每个矩形区域中的最大值进入下一层，而其他元素将不会进入下一层。所以最大池化提取特征图中响应最强烈的部分进入下一层，这种方式摒弃了网络中大量的冗余信息，使得网络更容易被优化。同时这种操作方式也常常丢失了一些特征图中的细节信息，所以最大池化更多保留些图像的纹理信息。

2.2 Average Pooling(平均池化)

2.2.1 定义

平均池化(Average Pooling)是将输入的图像划分为若干个矩形区域，对每个子区域输出所有元素的平均值。其定义如下：

平均池化就是计算图像区域的平均值作为该区域池化后的值，Resnet网络结构后一般会使用平均池化。

对于平均池化，我们需要把残差平分，传递到前边小区域的n个单元即可，不需要记录下元素在每个小区域中的位置。平均池化比较容易让人理解错的地方就是会简单的认为直接把梯度复制N遍之后直接反向传播回去，但是这样会造成loss之和变为原来的N倍，网络是会产生梯度爆炸的。

2.2.2 pytorch中的平均池化

torch.nn.AvgPool2d(kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True, divisor_override=None)

• kernel_size：池化窗口的大小。可以是一个整数，表示正方形窗口的边长，也可以是一个元组，表示不同维度的窗口大小。例如，(2, 2)表示宽和高为2的正方形窗口。

• stride：池化窗口的步幅。可以是一个整数，表示在所有维度上的步幅相同，也可以是一个元组，表示不同维度上的步幅。例如，(2, 2)表示在宽和高上的步幅为2。

• padding：输入张量的填充大小。可以是一个整数，表示在所有维度上的填充大小相同，也可以是一个元组，表示不同维度上的填充大小。例如，(1, 1)表示在宽和高上的填充大小为1。

• ceil_mode：是否采用向上取整的方式计算输出大小。如果为True，则输出大小会向上取整。默认为False。

• count_include_pad：是否将填充值计算在内。如果为True，则会将填充值计算在内。默认为True。

• divisor_override：用于覆盖默认的输出元素数。如果指定了该参数，则输出元素数将被覆盖为该值。默认为None。

2.2.3 使用示例

• 张量池化

import torch


# 定义输入数据张量，大小为 (batch_size, channels, height, width)
input_tensor = torch.randn(2, 3, 16, 16)

# 定义平均池化层，kernel_size 为池化核大小，stride 为步幅
avg_pool = torch.nn.AvgPool2d(kernel_size=2, stride=2)

# 对输入数据进行平均池化操作
output_tensor = avg_pool(input_tensor)

# 输出池化前后的结果张量大小
print("input_tensor:", input_tensor.shape)
print("output_tensor:", output_tensor.shape)

运行结果显示：

input_tensor: torch.Size([2, 3, 16, 16])
output_tensor: torch.Size([2, 3, 8, 8])

• 图片池化 

import torch
from PIL import Image
from torchvision.transforms import ToTensor
from torchvision.transforms.functional import to_pil_image
import matplotlib.pyplot as plt


# 读入示例图片并将其转换为 PyTorch 张量
img = Image.open('./data/lena.jpeg')
img_tensor = ToTensor()(img)

# 定义 AvgPool2d 函数，进行池化操作
avg_pool = torch.nn.AvgPool2d(kernel_size=2, stride=2)
img_pool = avg_pool(img_tensor.unsqueeze(0)).squeeze(0)

# 将池化后的张量转换为 PIL 图像并保存
img_pool_pil = to_pil_image(img_pool)

plt.subplot(121)
plt.imshow(img)
plt.title('original')
plt.axis('off')
plt.subplot(122)
plt.imshow(img_pool_pil)
plt.title('pool')
plt.axis('off')
plt.show()

 

2.2.4 总结

平均池化取每个矩形区域中的平均值，可以提取特征图中所有特征的信息进入下一层，而不像最大池化只保留值最大的特征，所以平均池化可以更多保留些图像的背景信息。

2.3 Global Average Pooling(全局平均池化)

在卷积神经网络训练初期，卷积层通过池化层后一般要接多个全连接层进行降维，最后再Softmax分类，这种做法使得全连接层参数很多，降低了网络训练速度，且容易出现过拟合的情况。在这种背景下，M Lin等人提出使用全局平均池化Global Average Pooling[1]来取代最后的全连接层。用很小的计算代价实现了降维，更重要的是GAP极大减少了网络参数(CNN网络中全连接层占据了很大的参数)。
论文地址: https://arxiv.org/pdf/1312.4400.pdf
代码链接: https://worksheets.codalab.org/worksheets

2.3.1 定义

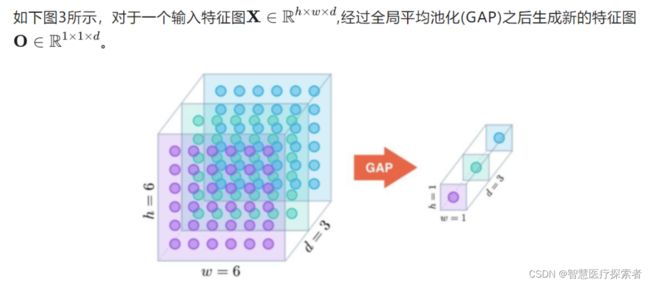
全局平均池化是一种特殊的平均池化，只不过它不划分若干矩形区域，而是将整个特征图中所有的元素取平均输出到下一层。其定义如下：

2.3.2 总结

作为全连接层的替代操作，GAP对整个网络在结构上做正则化防止过拟合，直接剔除了全连接层中黑箱的特征，直接赋予了每个channel实际的类别意义。除此之外，使用GAP代替全连接层，可以实现任意图像大小的输入，而GAP对整个特征图求平均值，也可以用来提取全局上下文信息，全局信息作为指导进一步增强网络性能。

2.4 Mix Pooling(混合池化)

论文地址: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.678.7068

2.4.1 定义

为了提高训练较大CNN模型的正则化性能，受Dropout(将一半激活函数随机设置为0)的启发，Dingjun Yu等人提出了一种随机池化Mix Pooling[2] 的方法，随机池化用随机过程代替了常规的确定性池化操作，在模型训练期间随机采用了最大池化和平均池化方法，并在一定程度上有助于防止网络过拟合现象。其定义如下：

2.4.2 总结

混合池化优于传统的最大池化和平均池化方法，并可以解决过拟合问题来提高分类精度。此外该方法所需要的计算开销可忽略不计，而无需任何超参数进行调整，可被广泛运用于CNN。

2.5 Stochastic Pooling(随机池化)

论文地址: https://arxiv.org/pdf/1301.3557
代码链接: https://github.com/szagoruyko/imagine-nn

2.5.1 定义

随机池化Stochastic Pooling[3] 是Zeiler等人于ICLR2013提出的一种池化操作。随机池化的计算过程如下：

    先将方格中的元素同时除以它们的和sum，得到概率矩阵。

    按照概率随机选中方格。

    pooling得到的值就是方格位置的值。

假设特征图中Pooling区域元素值如下(参考Stochastic Pooling简单理解)：

则这时候的poolng值为1.5。使用stochastic pooling时(即test过程)，其推理过程也很简单，对矩阵区域求加权平均即可。比如对上面的例子求值过程为为:

说明此时对小矩形pooling后的结果为1.625。在反向传播求导时，只需保留前向传播已经记录被选中节点的位置的值，其它值都为0,这和max-pooling的反向传播非常类似。本小节参考Stochastic Pooling简单理解[4]。

2.5.2 总结

随机池化只需对特征图中的元素按照其概率值大小随机选择，即元素值大的被选中的概率也大，而不像max-pooling那样，永远只取那个最大值元素，这使得随机池化具有更强的泛化能力。

2.6 Power Average Pooling(幂平均池化)

论文地址: http://proceedings.mlr.press/v32/estrach14.pdf

2.7 Detail-Preserving Pooling(DPP池化)

论文地址: Saeedan_Detail-Preserving_Pooling_in_CVPR_2018_paper.pdf
代码链接: https://github.com/visinf/dpp

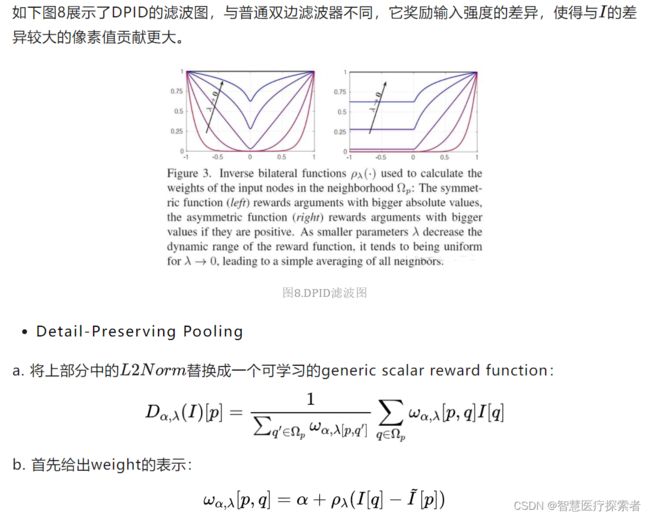
为了降低隐藏层的规模或数量，大多数CNN都会采用池化方式来减少参数数量，来改善某些失真的不变性并增加感受野的大小。由于池化本质上是一个有损的过程，所以每个这样的层都必须保留对网络可判别性最重要的部分进行激活。但普通的池化操作只是在特征图区域内进行简单的平均或最大池化来进行下采样过程，这对网络的精度有比较大的影响。基于以上几点，Faraz Saeedan等人提出一种自适应的池化方法-DPP池化Detail-Preserving Pooling[6]，该池化可以放大空间变化并保留重要的图像结构细节，且其内部的参数可通过反向传播加以学习。DPP池化主要受**Detail-Preserving Image Downscaling[7]**的启发。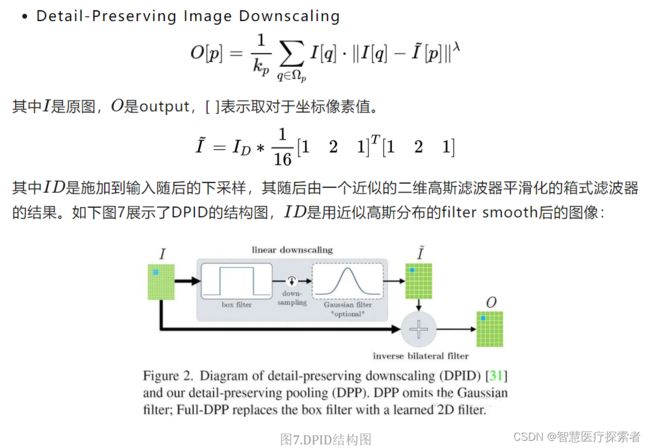

DPP池化允许缩减规模以专注于重要的结构细节，可学习的参数控制着细节的保存量，此外，由于细节保存和规范化相互补充，DPP可以与随机合并方法结合使用，以进一步提高准确率。

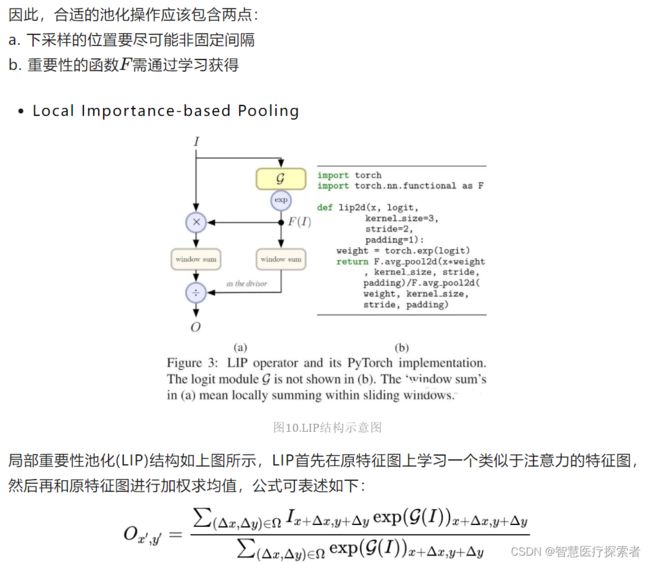
2.8 Local Importance Pooling(局部重要性池化)

论文地址: Gao_LIP_Local_Importance-Based_Pooling_ICCV_2019_paper.pdf
代码链接: https://github.com/sebgao/LIP

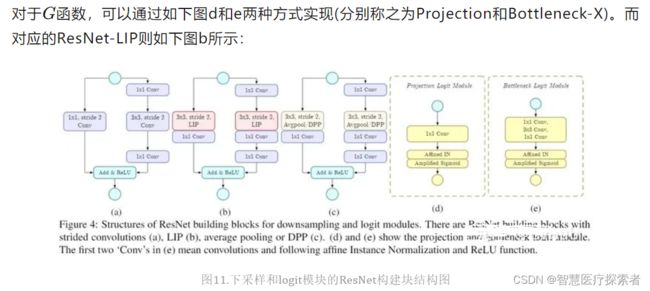
CNN通常使用空间下采样层来缩小特征图，以实现更大的接受场和更少的内存消耗，但对于某些任务而言，这些层可能由于不合适的池化策略而丢失一些重要细节，最终损失模型精度。为此，作者从局部重要性的角度提出了局部重要性池化Local Importance Pooling[8]，通过基于输入学习自适应重要性权重，LIP可以在下采样过程中自动增加特征判别功能。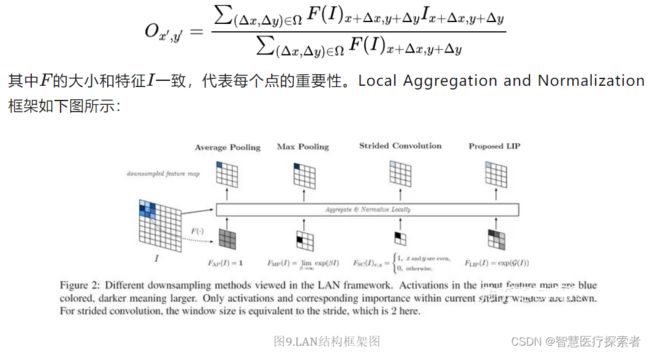

Local Importance Pooling可以学习自适应和可判别性的特征图以汇总下采样特征，同时丢弃无信息特征。这种池化机制能极大保留物体大部分细节，对于一些细节信息异常丰富的任务至关重要。

2.9 Soft Pooling(软池化)

论文地址: https://arxiv.org/pdf/2101.00440
代码链接: https://github.com/alexandrosstergiou/SoftPool

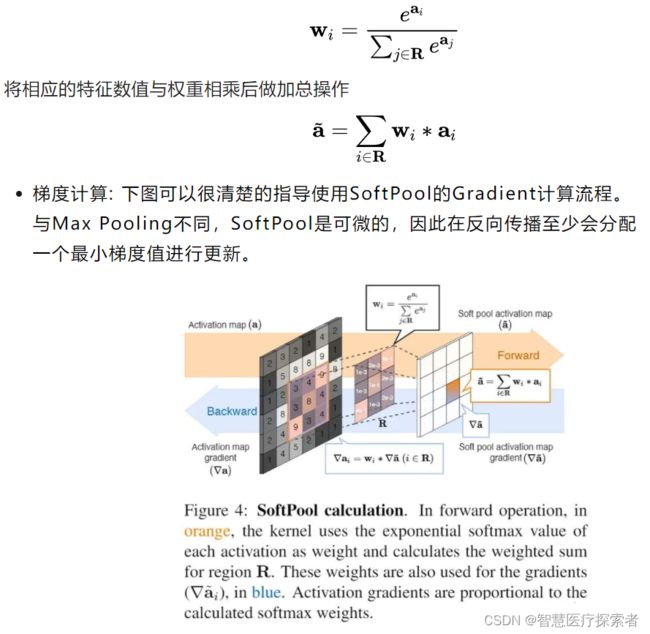
现有的一些池化方法大都基于最大池化和平均池化的不同组合，而软池化Soft Pooling[9] 是基于softmax加权的方法来保留输入的基本属性，同时放大更大强度的特征激活。与maxpooling不同，softpool是可微的，所以网络在反向传播过程中为每个输入获得一个梯度，这有利于提高训练效果。

SoftPool的计算流程如下：

• a. 特征图透过滑动视窗来框选局部数值
• b. 框选的局部数值会先经过指数计算，计算出的值为对应的特征数值的权重
• c. 将各自的特征数值与其相对应的权重相乘
• d. 最后进行加总

这样的方式让整体的局部数值都有所贡献，重要的特征占有较高的权重。比Max pooling(直接选择最大值)、Average pooling (求平均，降低整个局部的特征强度) 能够保留更多讯息。

    SoftPool的数学定义如下：

计算特征数值的权重，其中R为框选的局部区域，a为特征数值

作为一种新颖地池化方法，SoftPool可以在保持池化层功能的同时尽可能减少池化过程中带来的信息损失，更好地保留信息特征并因此改善CNN中的分类性能。大量的实验结果表明该算法的性能优于原始的Avg池化与Max池化。随着神经网络的设计变得越来越困难，而通过NAS等方法也几乎不能大幅度提升算法的性能，为了打破这个瓶颈，从基础的网络层优化入手，不失为一种可靠有效的精度提升手段。